傅里叶变换与卷积:揭示频域的魔力
需积分: 49 172 浏览量
更新于2024-09-09
收藏 988KB DOCX 举报
"傅里叶与卷积公式的概念及其应用"
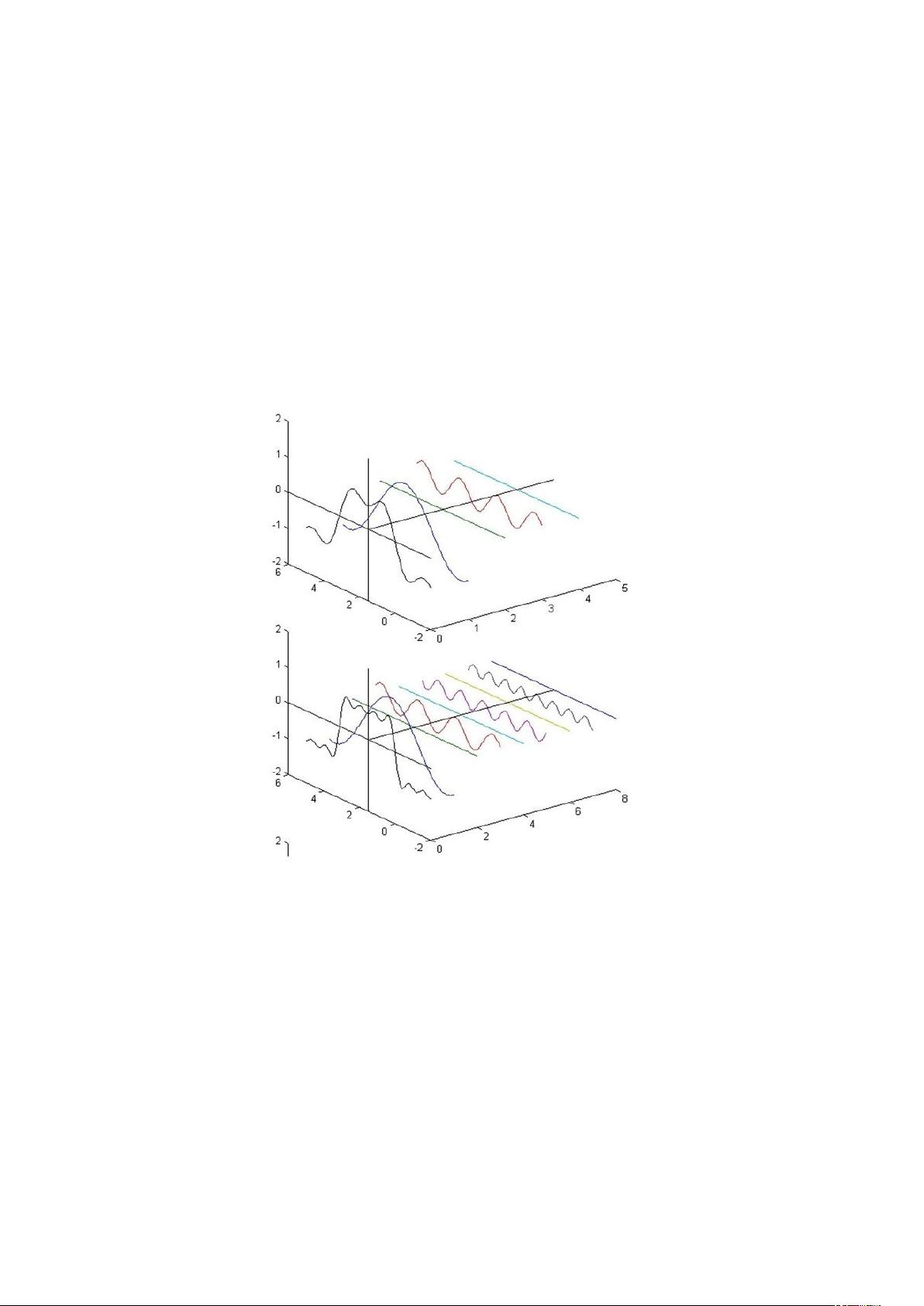
傅里叶变换是数学中的一个重要工具,特别是在信号处理、图像处理、通信工程等领域有着广泛的应用。它将一个在时间或空间域(时域或空域)的函数转换为其在频率域的表示。傅里叶变换的核心思想是将复杂的时域信号分解为简单正弦波的叠加,这些正弦波对应于不同的频率成分。
傅里叶变换的基本公式可以表示为:
\[ F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt \]
其中,\( f(t) \) 是原始的时域信号,\( F(\omega) \) 是对应的频域表示,\( \omega \) 是频率变量,\( j \) 是虚数单位。通过傅里叶变换,我们可以分析信号的频率成分,了解信号由哪些频率的正弦波组成,以及它们的幅度和相位。
频域分析的一个显著优点是简化复杂运算。例如,时域中的微积分操作在频域中可以转化为简单的乘法和除法。这是因为傅里叶变换具有线性和共轭对称性,这使得某些计算变得容易得多。比如,滤波操作,即从信号中去除或增强特定频率成分,时域中可能非常复杂,但在频域只需对相应的频率分量进行加减乘除即可实现。
卷积是另一个与傅里叶变换密切相关的概念。卷积在信号处理中用于描述两个函数相互作用的结果,如两个信号的叠加或影响。卷积的傅里叶变换满足互换性,即:
\[ (f * g)(t) \Leftrightarrow F(\omega)G(\omega) \]
这意味着在时域中两个函数的卷积对应于它们在频域的乘积,反之亦然。这一性质在设计滤波器和分析系统响应时非常有用。
傅里叶级数是傅里叶变换的特例,用于将周期性的连续函数表示为有限个正弦波的和。对于非周期函数,我们使用傅里叶变换,它将其转换为非周期的频域表示。欧拉公式在这里起到了关键作用,它建立了三角函数与复数指数函数之间的联系:
\[ e^{j\theta} = \cos(\theta) + j\sin(\theta) \]
欧拉公式揭示了正弦和余弦函数的复数本质,为傅里叶分析提供了深刻的几何解释。在频域中,每个频率成分可以用一个在复平面上旋转的点来表示,而傅里叶变换就是这个旋转点在不同时间的轨迹。
傅里叶变换和卷积是理解和处理周期性和非周期性信号的基础,它们在现代科技中扮演着不可或缺的角色,从音频处理到图像分析,再到通信系统的建模,都离不开这两个概念。通过深入理解这些理论,我们可以更有效地解析和操纵各种类型的数据。
317 浏览量
271 浏览量
点击了解资源详情
725 浏览量
2022-09-24 上传
317 浏览量
滴水穿地核
- 粉丝: 7
- 资源: 8
最新资源
- python-3.4.4
- elemental-lowcode:元素低码开发平台
- Logger:记录工具
- SheCodes-WeatherApp:挑战3
- 阿宾贝夫前端测试
- 银灿IS917U盘PCB电路(原理图+PCB图)-其它其他资源
- registry-url:获取设置的npm注册表URL
- ST-link驱动.rar
- keen-gem-example:一个 Sinatra 应用程序,使用敏锐的 gem 异步发布事件
- 行业分类-设备装置-一种抗菌纸.zip
- Pearl-Hacks-2021:线框的htmlcss骨架
- a2s-rs:源代码查询的Rust实现
- DotFiles:我的Dotfiles <3
- Magisk Manager-20.1.zip
- ScheduleReboot:此实用程序用于在特定时间重新引导计算机,解决了在目标时间内处于睡眠模式的计算机在唤醒后实施重新引导的问题。
- Online-Face-Recognition-and-Authentication:Hsin-Rung Chou、Jia-Hong Lee、Yi-Ming Chan 和 Chu-Song Chen,“用于人脸识别和认证的数据特定自适应阈值”,IEEE 多媒体信息处理和检索国际会议,MIPR 2019