离散傅里叶变换的快速算法:FFT详解
166 浏览量
更新于2024-06-29
收藏 1.02MB PPTX 举报
"华侨大学自动化专业数字信号处理ppt3(与“抽取”相关共44张).pptx"
本文主要探讨了数字信号处理中的快速傅里叶变换(FFT)算法,特别是与“抽取”相关的基2时间抽取和基2频率抽取FFT算法。在离散傅里叶变换(DFT)计算中,当处理的序列较长时,直接计算会导致大量的复数乘法和加法,从而消耗大量计算资源。因此,提出了FFT算法来提高运算效率。
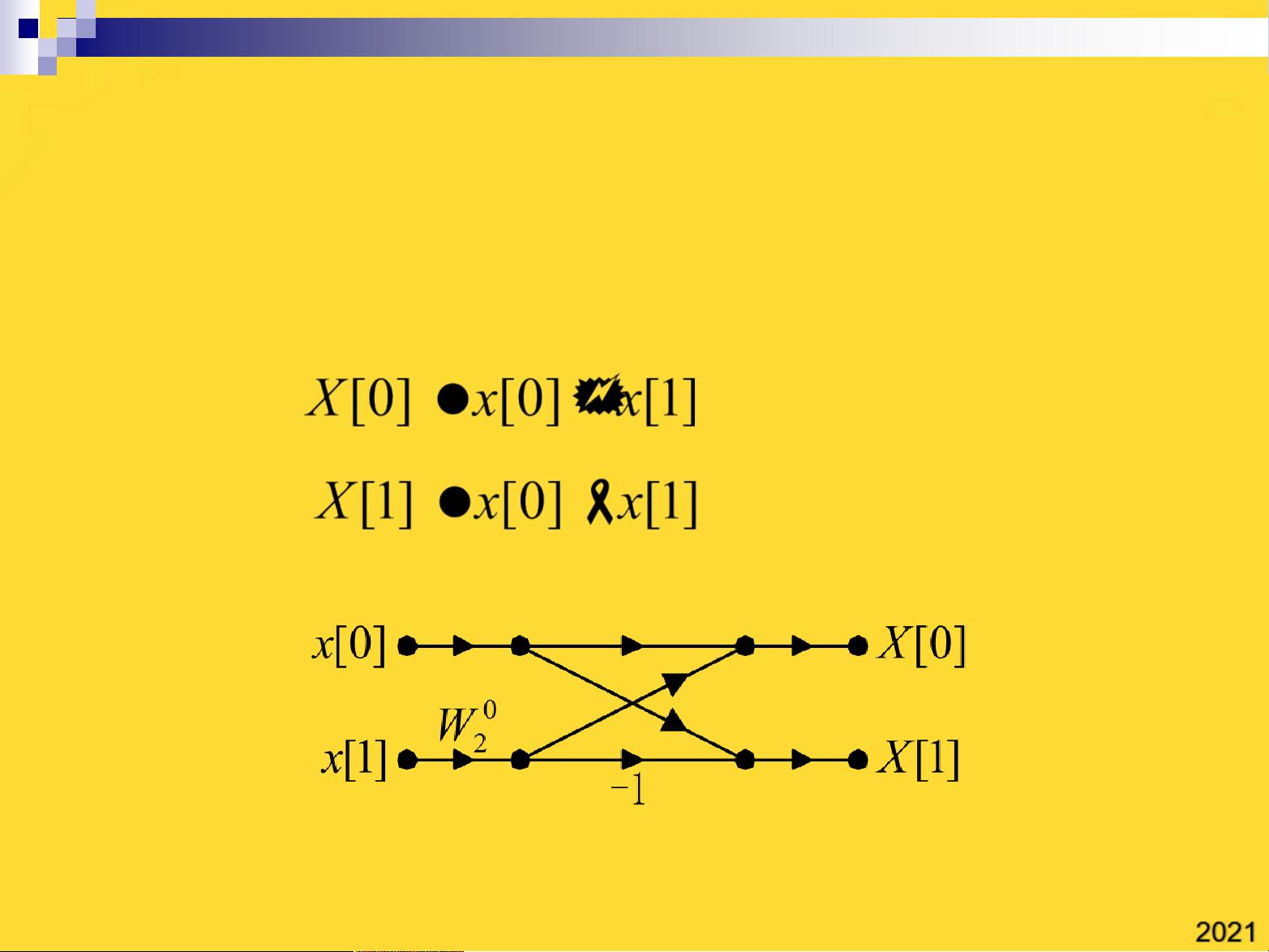
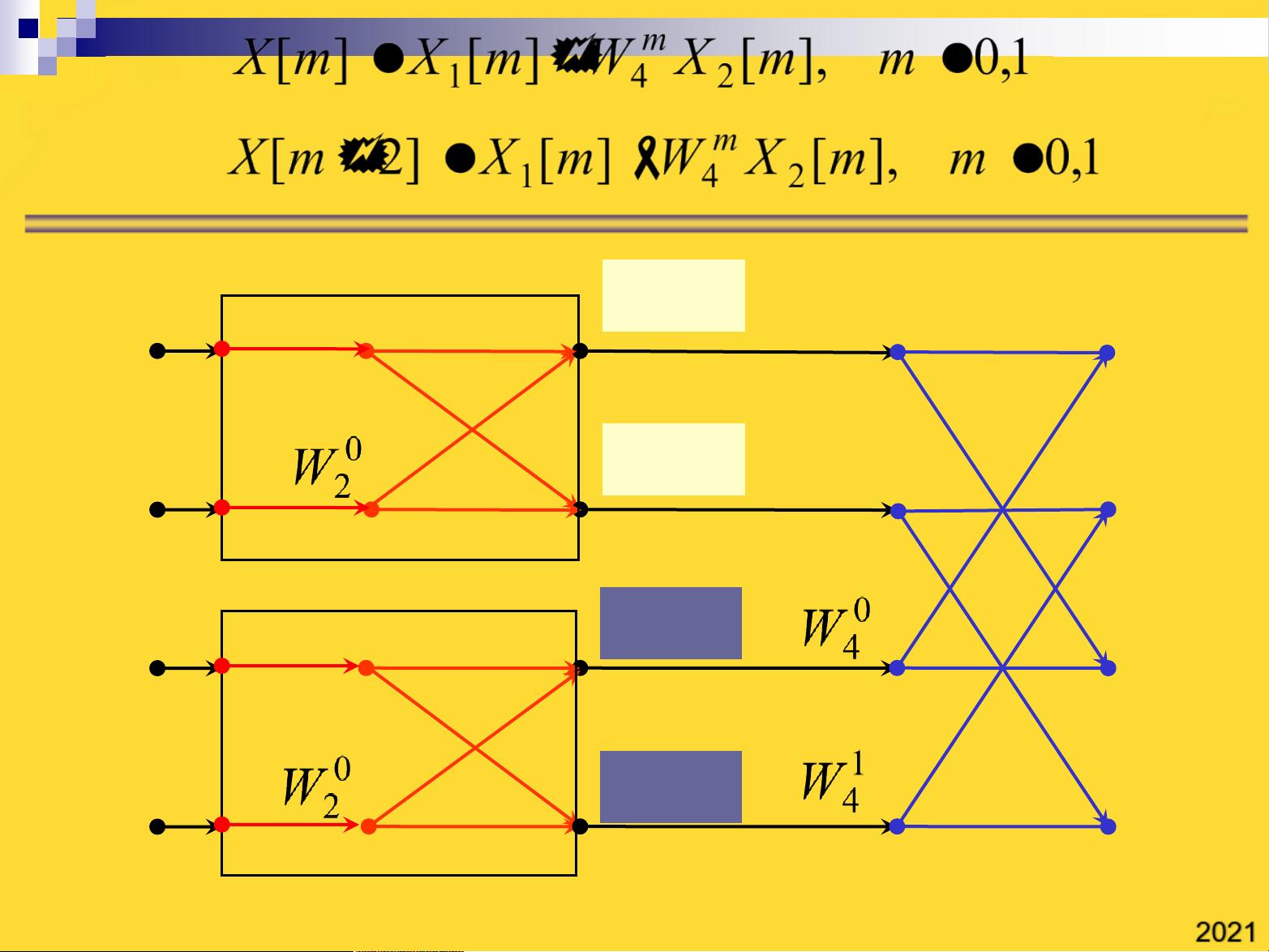
一、基2时间抽取FFT算法
基2时间抽取FFT算法是通过将长序列分解为多个较短的序列,然后分别进行DFT运算,最后将结果组合得到原始序列的DFT。其基本思想是利用DFT的周期性和旋转因子的特性,将N点序列分解为两个N/2点序列。此算法的特点在于其计算复杂度较低,减少了复数乘法的数量,大大提高了计算效率。
二、基2频率抽取FFT算法
基2频率抽取FFT算法与时间抽取不同,它是在频域内进行操作。首先计算完整的N点DFT,然后根据所需频率位置选取部分结果,形成所需的N/2点DFT。这种方法同样降低了计算复杂度,但与时间抽取相比,它更适用于已知需要分析的频率范围的情况。
三、FFT算法的实际应用
FFT在众多领域有广泛应用,包括音频和图像处理、通信系统、滤波器设计、信号检测等。例如,在音频处理中,FFT可以用于频谱分析,识别音频信号的频率成分;在通信中,它可以用于解调和调制;在滤波器设计中,通过FFT计算可以快速得到滤波器的频率响应。
四、基4时间抽取FFT算法
基4时间抽取FFT算法是基2算法的扩展,适用于更高效地处理4的幂次的序列长度。其原理类似,将序列分解为更小的4点序列,通过多次计算和组合实现FFT。
五、混合基FFT算法
混合基FFT算法结合了不同基的特性,比如基2和基4,以优化特定序列长度的计算效率。这种算法在处理非2的幂次长度序列时特别有用,可以进一步减少计算量。
六、示例计算
举例来说,给定序列x[k]={1,2,3,4},使用基2时间抽取FFT算法,可以先将其分解为x1[k]={1,3}和x2[k]={2,4},分别计算它们的2点DFT,然后通过合成步骤得到4点序列的DFT。
总结,FFT算法通过巧妙的时间抽取和频率抽取策略,极大地优化了DFT的计算过程,尤其在处理大长度序列时,显著提高了计算效率。这些算法在实际的数字信号处理中扮演着核心角色,为各种信号分析和处理任务提供了基础工具。
2022-11-14 上传
matlab大师
- 粉丝: 2789
- 资源: 8万+