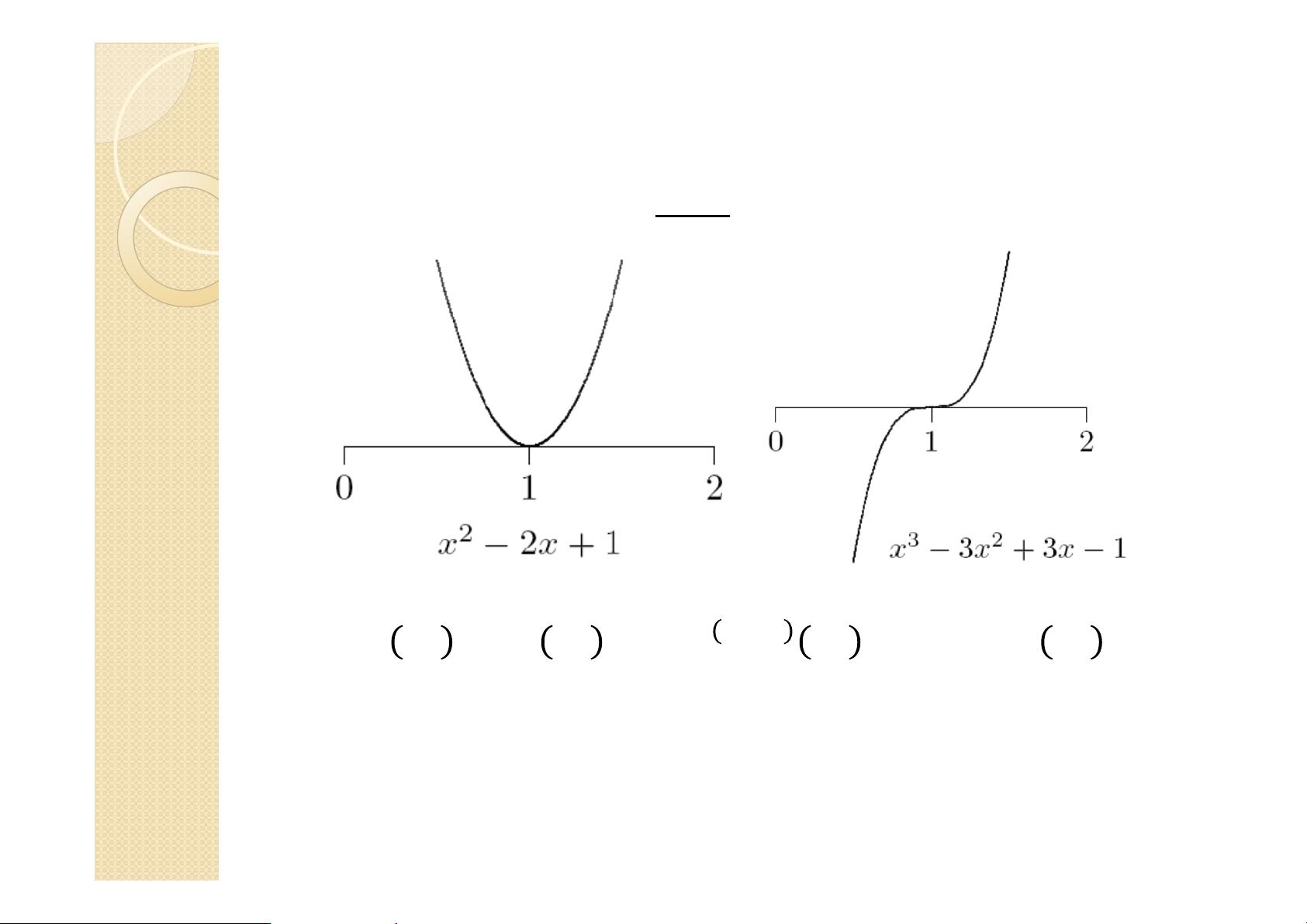非线性方程求解方法：从二分法到牛顿法

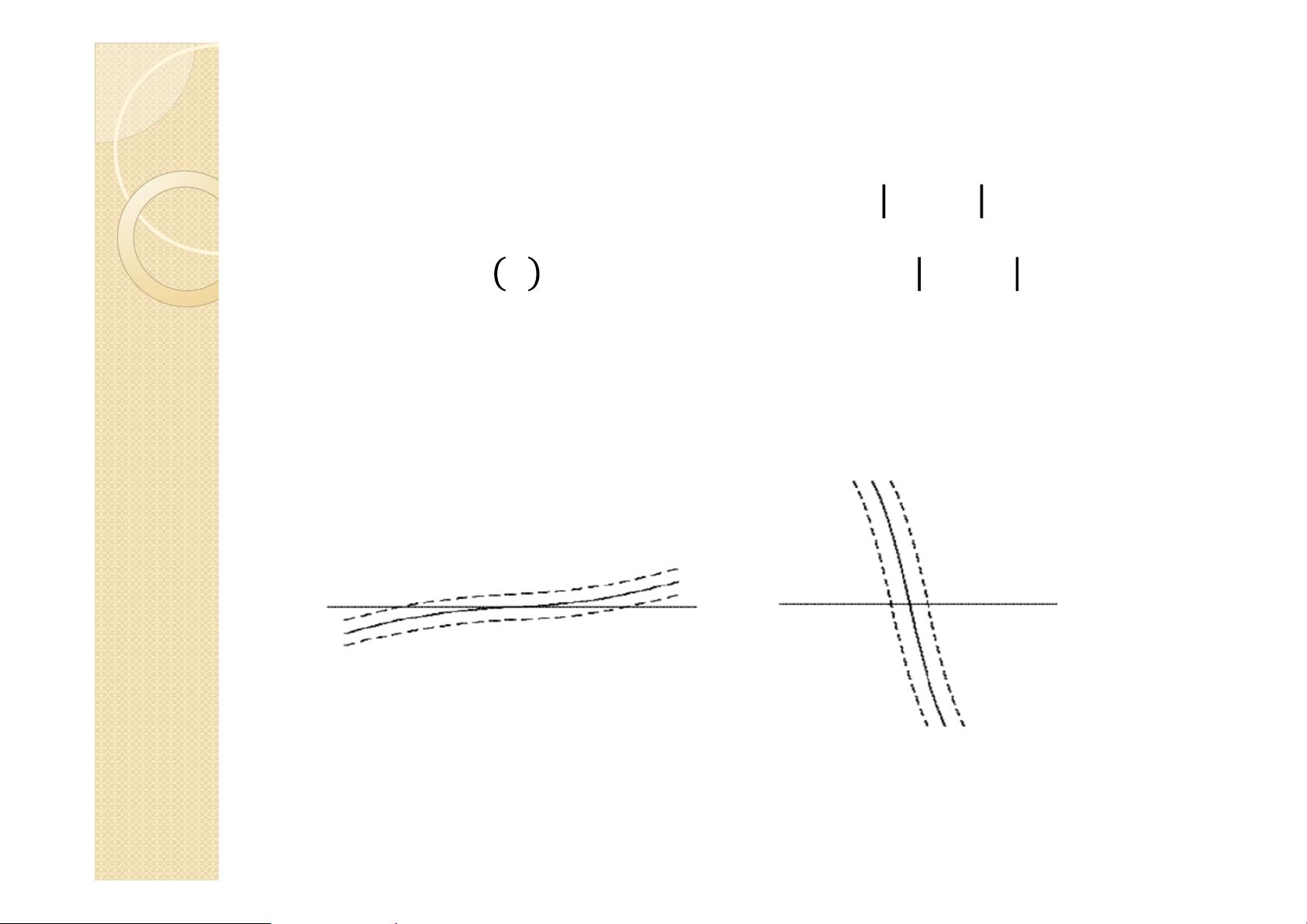
"数据与算法课程：12 非线性方程.pdf" 这篇文档主要探讨了非线性方程的解决方法，这是数据分析和算法领域的重要组成部分。非线性方程广泛存在于自然界中，很多复杂的物理、化学及工程问题不能简单地用线性模型描述。例如，运动物体的空气阻力与其速度的平方成正比，气体的范德华状态方程描述了压强、体积和温度之间的非线性关系。因此，理解和求解非线性方程对于科学计算至关重要。 文档首先介绍了非线性方程的基本概念，它定义为一个非线性函数等于零的解，即找到变量的值使函数值为零。这通常被称为方程求根或零点问题。非线性方程组可能表现为欠定或超定，与线性方程组一样，需要利用优化技术来求解。文档特别强调了一维非线性方程问题，因为其解的情况相对简单，但也具有多样性，如无解、一个解、多个解甚至无限多个解。 接着，文档提到了解的特性，特别是对于一维非线性方程，解可能有不同的情形，这可以通过介值定理来证明。介值定理指出，如果一个连续函数在区间两端的值符号相反，那么在这个区间内至少存在一点使得函数值为零。这个定理为求解非线性方程提供了一种理论依据。 文档还讨论了不动点和压缩映射的概念，不动点是指被函数映射到自身的一个点。压缩映射是一个函数，使得在其定义域内的任何两点之间，映射的距离小于原始距离的某个常数倍。压缩映射定理表明，在满足一定条件的闭集上，压缩映射必然存在唯一的不动点。这个定理是不动点迭代法的基础，非线性方程的求解经常采用迭代方法，如二分法、不动点迭代、牛顿法和准牛顿法。 具体到解法，文档提及了几种常用的技术： 1. 二分法：一种简单的迭代方法，适用于函数在其定义区间内连续且单调的方法。 2. 不动点迭代：基于压缩映射定理，通过不断应用函数并趋近于不动点来找到方程的解。 3. 牛顿法：利用函数的导数信息，构造切线来逼近零点，效率较高但需要函数及其导数的连续性。 4. 准牛顿法：是对牛顿法的一种改进，当导数信息难以获取时，通过近似Hessian矩阵来实现。 这些方法在实际问题中各有优缺点，选择哪种方法取决于问题的具体情况，包括函数的性质、解的稳定性以及计算资源等。 总结起来，该文档深入浅出地介绍了非线性方程的理论基础和解决策略，对于学习算法和数值分析的学员来说，提供了宝贵的教育资源。了解和掌握这些方法对于处理复杂的数据建模和计算问题至关重要。