傅里叶变换详解：从级数到非周期函数的扩展

"这篇资料详细阐述了傅里叶变换的概念，从傅里叶级数的基础出发，探讨了如何将周期性函数用复指数形式表示。它还提到了非周期性函数的傅里叶变换，以及如何处理那些在足够大绝对值的t处为零的函数。" 傅里叶变换是一种在数学、物理和工程领域广泛使用的分析工具，它能够将一个函数从时域或空间域转换到频域，揭示信号或图像的频率成分。傅里叶变换的起源可以追溯到傅里叶级数，它最初是用于解析周期性函数的，但后来发展成为适用于更广泛函数的理论。 傅里叶级数是将周期性函数分解为正弦和余弦函数的无限级数，而傅里叶变换则进一步扩展了这个概念，允许使用所有可能周期的复指数函数（或等效地，正弦和余弦函数）来表达非周期函数。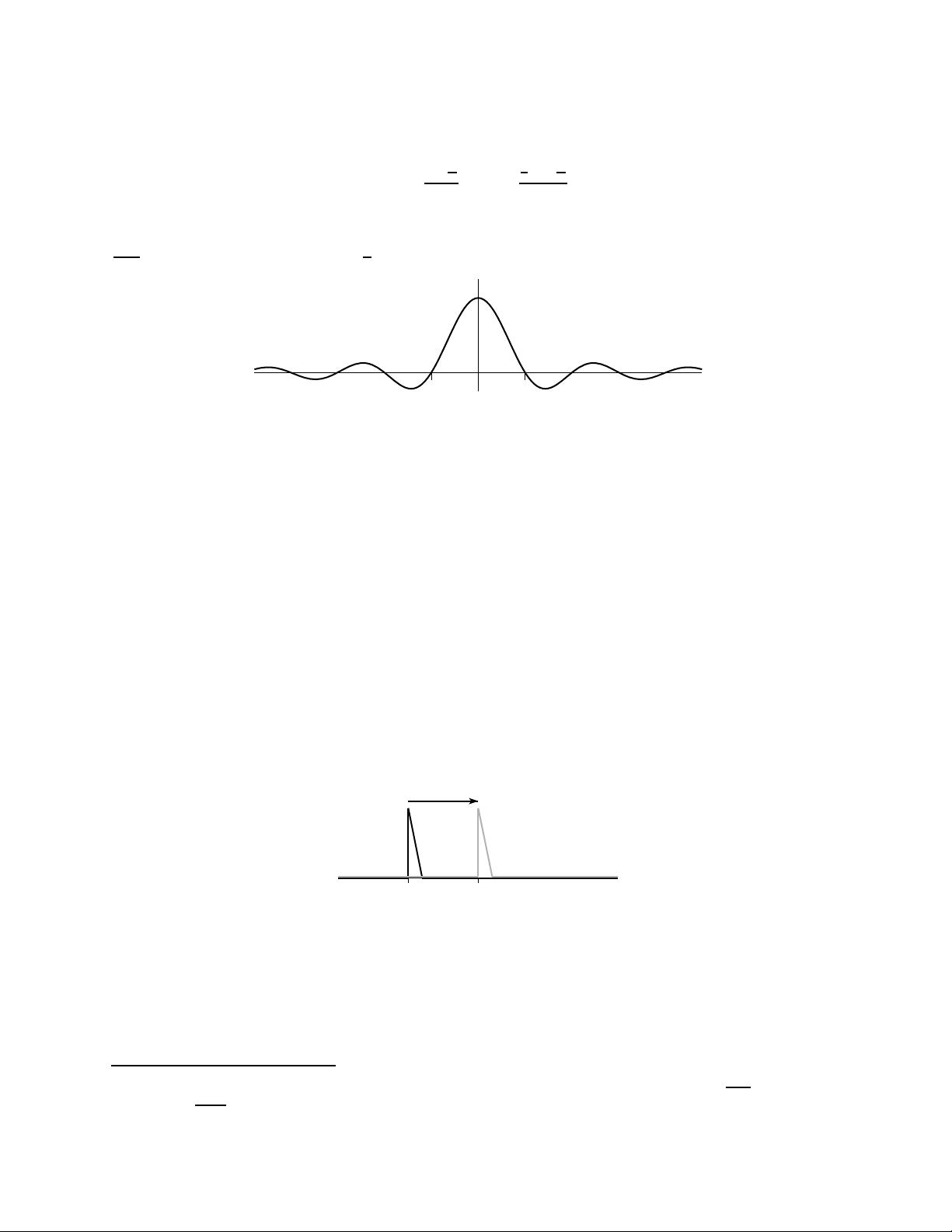在给定的资料中，周期性函数的傅里叶级数公式被展示为： \[ f(t) = \sum_{k=-\infty}^{\infty} c_k e^{ik\pi \ell t} \] 其中，\( c_k \) 是傅里叶系数，可以通过下面的积分公式计算得到： \[ c_k = \frac{1}{2\ell} \int_{-\ell}^{\ell} f(t) e^{-ik\pi \ell t} dt \] 傅里叶变换的核心在于，它可以将任何足够光滑且在足够大的绝对值 \( |t| \) 处为零的函数 \( f(t) \) 表示为复指数形式的无穷级数。如果函数不是周期性的，我们可以考虑所有可能的周期，不再局限于固定的 \( 2\ell \)。这使得傅里叶变换能够应用于更复杂的非周期信号分析。 在实际应用中，傅里叶变换特别有用，因为它能够帮助我们理解和处理信号的频率成分。例如，在音频处理中，傅里叶变换可以揭示声音信号中的不同频率分量；在图像处理中，它可以分析图像的频谱特性，从而进行滤波、压缩等操作。 对于那些在足够大的 \( |t| \) 处为零的函数，可以选取一个大于 \( L \) 的值，使得 \( f(t) = 0 \) 对所有 \( |t| \geq L \) 成立。这种情况下，函数的傅里叶变换依然可以被定义，并且可以推导出更一般的结果。通过这种方式，傅里叶变换的理论能够应用于更广泛的函数类别，不仅限于那些在有限区间内定义的函数。 傅里叶变换是数学分析的重要工具，它提供了将复杂信号或函数分解为简单频率成分的方法，从而在各种科学和工程领域中发挥着至关重要的作用。