图论算法精要：强连通分量、欧拉回路与拓扑排序详解

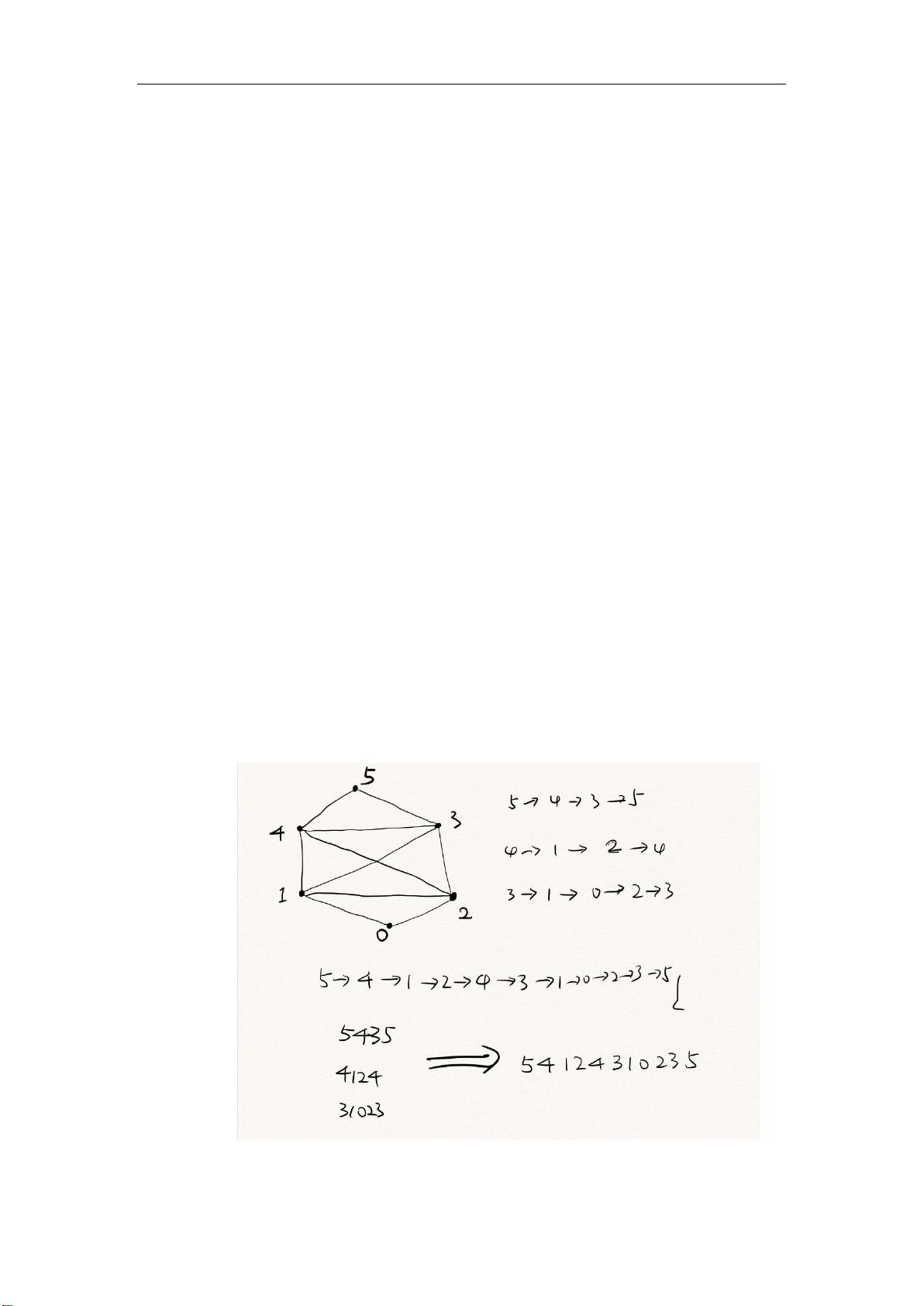
经典算法笔记1主要涵盖了图论中的几个核心概念和问题解决方法，包括最小费用最大流、强连通分量、欧拉回路、拓扑排序以及关键路径与关键节点（AOE网）。让我们逐一深入解析这些重要算法。 1. **最小费用最大流**： 最小费用最大流问题源于实际中的物流或网络流问题，其中每条边都有容量限制且带有成本。该问题的目标是在不违反边的容量约束条件下，找到使总成本最低的流量分配方案。算法通常使用Ford-Fulkerson方法或Edmonds-Karp算法来求解。 2. **求有向图的强连通分量**： 通过预后序遍历（pre[]和post[]数组）和全局变量clock，首先反向构建图Gr，然后对每个节点调用explore函数进行深度优先搜索（DFS），填充pre和post值。最后，根据post数组降序排序并应用无向图的连通分量算法，能确保得到正确的强连通分量。 3. **欧拉回路与简单路径**： 欧拉回路是图中一条经过所有边恰好一次的路径，若所有节点度数均为偶数，存在欧拉回路。通过无回溯DFS寻找，如果所有边都被访问，说明找到了欧拉回路；否则，继续寻找未访问过的路径，直到完成遍历。 4. **拓扑排序**： 在有向无环图（DAG）中，拓扑排序是一种线性化的表示方式，它确定了一个节点何时可以在其他节点之前开始执行。通过先处理入度为0的节点，逐步将它们添加到排序序列中，并更新后继节点的依赖关系。 5. **关键路径和关键节点（AOE网）**： AOE网是活动-资源-时间网络，用于项目管理中的计划。关键路径是网络中耗时最长的路径，决定了整个项目的最早完成时间。关键节点是关键路径上的节点，其延误可能导致整个项目的延误。通过拓扑排序找出节点的最早和最迟开工时间，计算关键路径和关键节点。 这些算法在软件工程、数据结构、计算机网络等领域具有广泛应用，理解和掌握它们对于解决实际问题至关重要。理解算法背后的原理和应用场景，能帮助提升编程效率和解决问题的能力。