矩阵黎卡提微分方程-最优控制课件及边界条件，探讨线性函数状态变量的最优控制问题

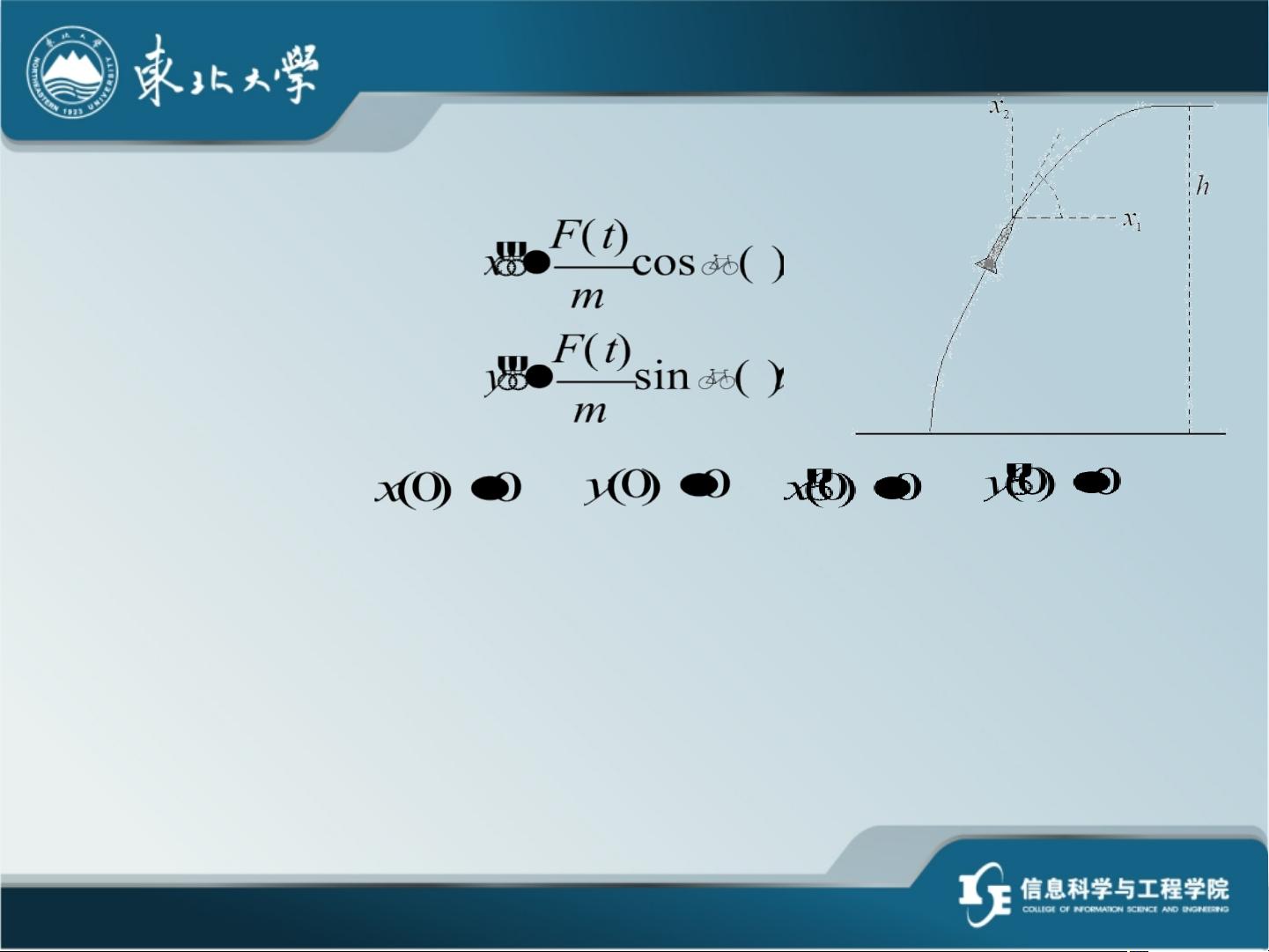
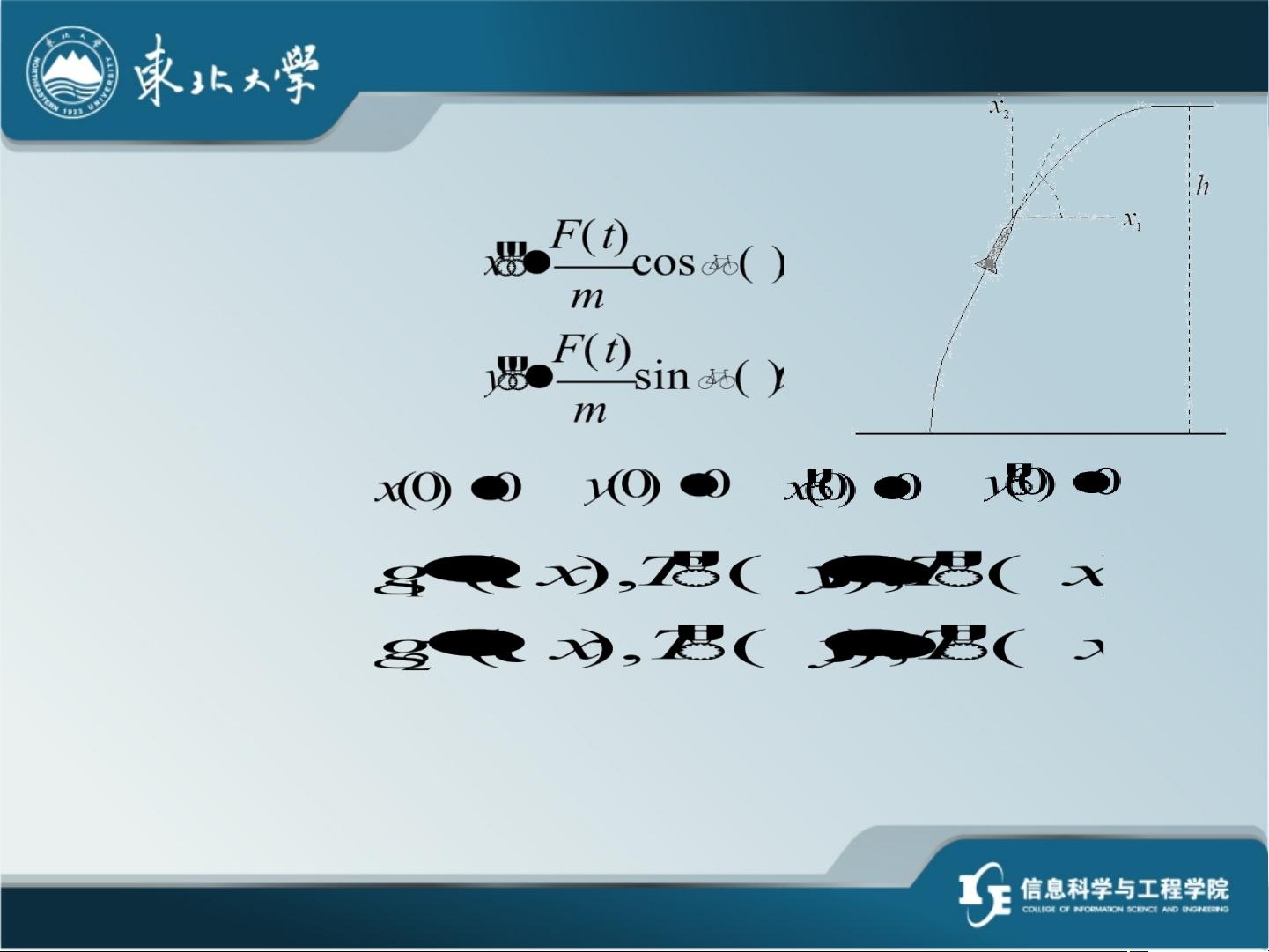
矩阵黎卡提微分方程-最优控制课件是关于最优控制中的矩阵黎卡提微分方程的介绍。最优控制是一种通过选择最佳控制规律来实现系统最优性能的方法。在最优控制中，状态变量是一个线性函数，并且可以借助状态变量的线性反馈来实现闭环最优控制。 在最优控制中，我们通常遇到一些边界条件，这需要我们在求解最优控制问题时加以考虑和处理。此外，我们还会涉及到对称半正定矩阵和线性二次型性能指标的最优控制方法。 现代控制理论中，最优控制理论被视为一个重要的组成部分。它在20世纪50年代得到了发展，并成为控制系统理论研究的关键问题之一。最优控制问题的研究对象是给定一个控制系统，在某种意义上选择最佳控制规律，使系统在性能指标上达到最优。最优控制的研究者们提出了一些严格的数学方法来解决这个问题，并且在工程应用中取得了显著的效益。 最优控制问题的求解可以借助变分方法、最大值原理、动态规划等技术。其中，变分方法在求解最优控制问题中有重要的应用，它通过极小化一个泛函得到最优控制规律。最大值原理是最优控制中的一个重要原理，通过在状态变量和伴随变量上施加一些约束条件，可以得到最优控制规律的形式。动态规划方法是一种通过递推求解的优化方法，在最优控制问题中也有广泛应用。 此外，在最优控制问题中，线性二次型性能指标的最优控制方法也是一个重要的研究方向。它主要利用线性二次型性能指标来描述系统的性能，采用特殊的控制规律来优化系统的性能。 另外，快速控制系统也是最优控制的一个分支领域，它主要研究如何在快速响应的控制系统中实现最优性能。快速控制系统在现代工业控制中有广泛的应用，它能够提高系统的响应速度、稳定性和鲁棒性。 总之，最优控制理论是现代控制理论中的重要组成部分。通过研究最优控制问题，我们可以选择最佳的控制规律，使系统在某种意义上达到最优性能。最优控制理论在各个领域中都有应用，可以帮助工程师设计高性能的控制系统，取得显著的效益。矩阵黎卡提微分方程是最优控制中常用的一种方法，在求解最优控制问题中起到重要的作用。