最小二乘法在自适应滤波中的应用

"最小二乘法是用于求解线性回归问题的一种常用算法，尤其在处理自适应滤波和信号处理问题中具有重要应用。它旨在通过调整模型参数，使得模型预测值与实际观测值之间的误差平方和最小化。本资料主要介绍了最小二乘法及其在自适应滤波器中的应用，特别是递推最小二乘(RLS)算法、最小二乘格形(LSL)算法和快速横式滤波器(FTT)算法。" 在最小二乘法中，目标是找到一组参数，使得误差平方和达到最小。在自适应滤波器的背景下，这个误差是指滤波器输出与所需信号之间的差异。传统上，最小均方误差准则被用来更新滤波器权重，但这种方法依赖于对输入数据长期统计特性的了解。最小二乘法则提供了一种直接基于有限数据集优化滤波器的方法，因此它能给出针对特定数据集的“精确”最佳滤波器。 递推最小二乘(RLS)算法是一种在线学习算法，它在每一步迭代中都更新滤波器权重，以最小化过去所有数据点的误差平方和，同时考虑到新数据的影响。RLS算法的优点在于它提供了快速收敛和良好的稳定性。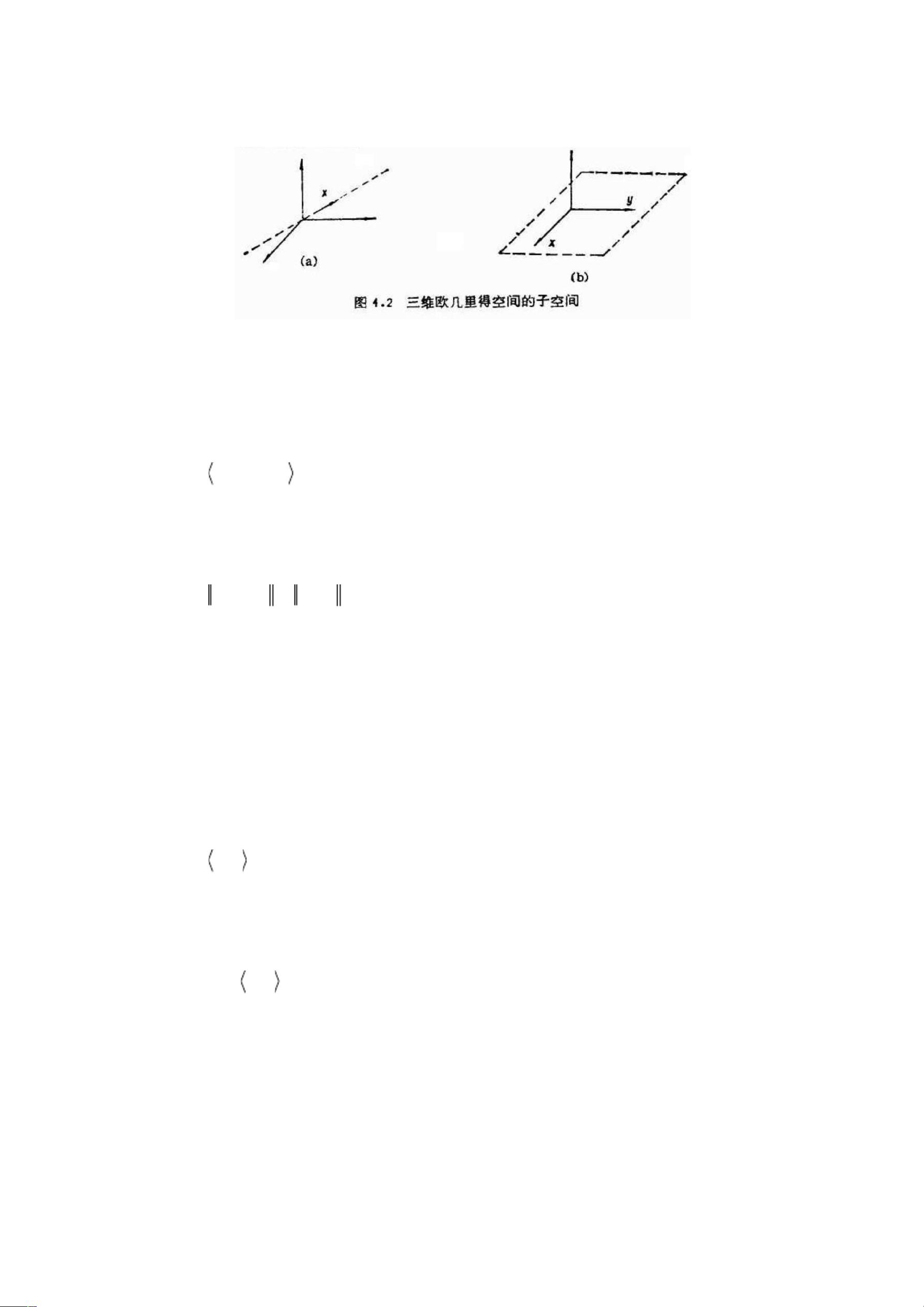 线性空间的概念在理解最小二乘方法中至关重要，因为它允许我们将问题转化为线性代数的形式。在这个基础上，最小二乘格形(LSL)算法和快速横式滤波器(FTT)算法被提出。LSL算法利用格形结构来高效地计算最小二乘解，而FTT算法则提供了一种快速的算法，减少了计算复杂性，适用于大规模数据集。 在第4.1节中，最小二乘滤波方程被建立，通过定义线性滤波器的权重w(n)来估计需要的信号d(i)。误差项e(i)表示实际信号与估计信号的差值，而性能函数η(n)是所有误差平方和的累积，其最小化给出了最优的w(n)值。λ是加权因子，用来平衡新旧数据的影响，确保算法能够适应不断变化的环境。 最小二乘法在处理自适应滤波问题时提供了一种实用且灵活的工具，通过不同算法的实现，可以有效地适应各种数据集和应用场景。RLS、LSL和FTT算法分别从不同的角度解决了最小二乘问题，为实际工程应用提供了多样化的解决方案。