有限时间粒子群优化算法：气味源定位新方法

"本文提出了一种有限时间粒子群优化算法（FPSO）用于气味源定位。该算法基于粒子群优化（PSO）的连续时间模型，通过引入非线性阻尼项实现有限时间内的收敛，并通过调整参数增强探索能力。通过Lyapunov方法分析了算法的有限时间收敛性，然后利用线性矩阵不等式（LMI）方法得出离散时间FPSO算法的收敛条件。数值模拟结果证明了该FPSO算法在解决气味源定位问题上的有效性，特别是在处理不适定函数和基准函数时表现出优良性能。" 粒子群优化（PSO）是一种模拟自然界群体行为的全局优化算法，由多个智能体（粒子）组成，它们在搜索空间中移动并更新其位置，以寻找最优解。在传统PSO中，粒子的速度和位置会根据自身和全局最佳位置进行更新，随着时间的推移逐渐收敛到最优解。 在本文中，作者针对PSO算法的局限性，提出了一种连续时间有限时间PSO（FPSO）算法。关键创新在于引入了非线性阻尼项，这使得算法能够在预设的时间内达到收敛，提高了算法的效率。同时，为了提高FPSO在搜索空间中的探索能力，引入了调谐参数，以平衡局部搜索与全局搜索的能力，避免早熟收敛。 为了从连续时间模型转换到离散时间模型，作者采用了特定的离散化方案。离散时间FPSO的收敛条件通过线性矩阵不等式（LMI）方法进行分析，这是一种在控制理论中常用的技术，可以有效地处理系统稳定性和性能的问题。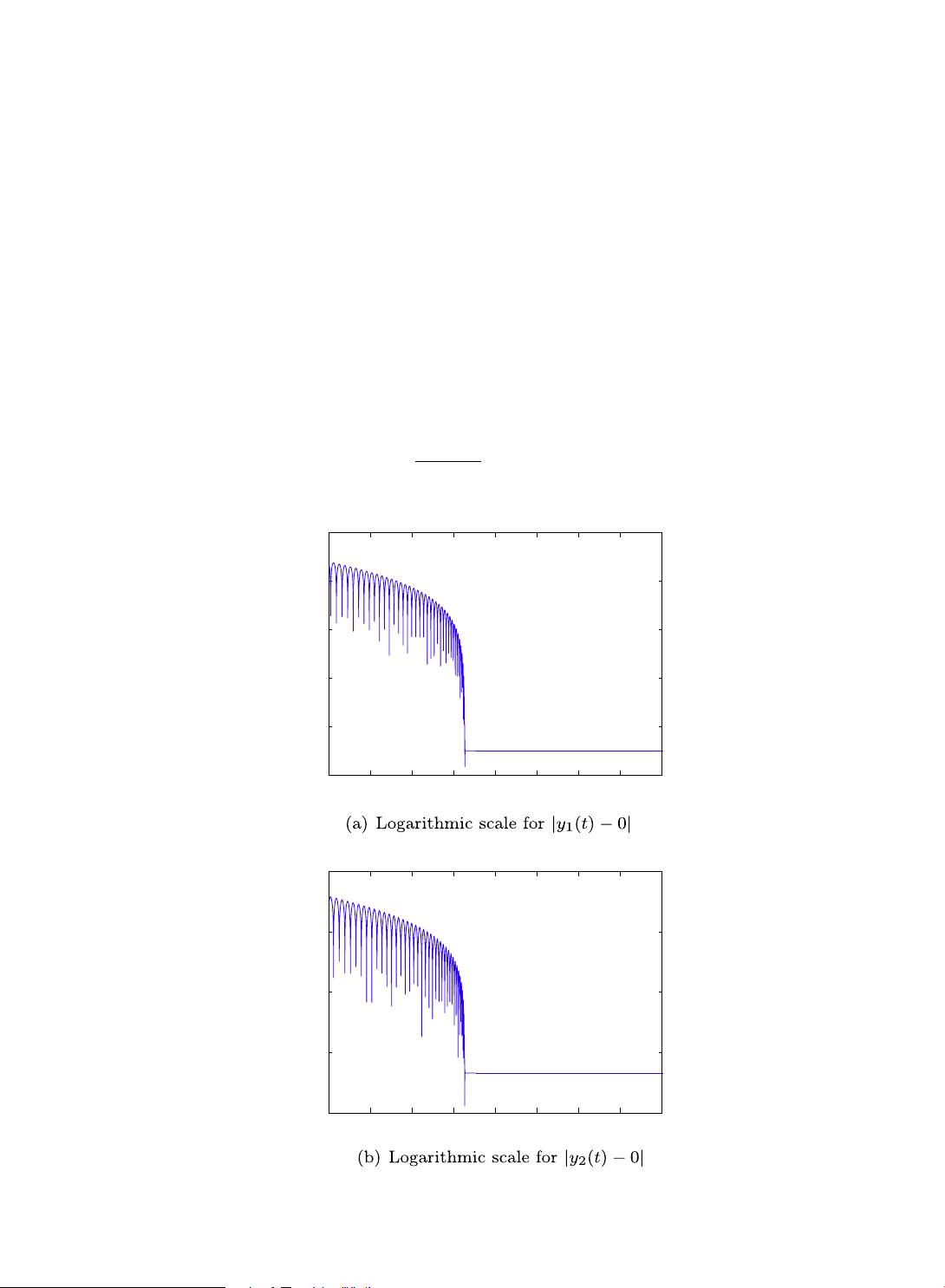 实验部分，作者使用两个不适定函数和二十五个基准函数来评估FPSO算法的性能。不适定函数通常具有多个局部极小值，对优化算法的性能提出挑战。而基准函数则覆盖了各种复杂度和维度，进一步验证了FPSO算法在不同情况下的适用性。最后，通过模拟气味源定位问题，展示了FPSO在实际应用中的有效性，证明了其在多机器人系统中寻找目标位置的潜力。 这篇论文提出的有限时间粒子群优化算法为解决复杂优化问题，特别是气味源定位这类实时性要求高的任务，提供了一种新的、高效的工具。通过引入非线性阻尼和调谐参数，增强了算法的收敛速度和探索能力，对于未来的多机器人协同定位和其他实时优化问题的研究具有重要的参考价值。