利用互信息最大化进行多模态医学图像配准

需积分: 10 79 浏览量更新于2024-09-08 收藏 625KB PDF 举报

"maesmiimageregpdf-maes_mi_image_reg.pdf——使用互信息最大化的多模态医学图像配准" 这篇论文"Multimodality Image Registration by Maximization of Mutual Information"发表在1997年4月的IEEETRANSACTIONSONMEDICALIMAGING期刊第16卷第2期，作者包括Frederik Maes、Andr´e Collignon、Dirk Vandermeulen、Guy Marchal和Paul Suetens，他们都是IEEE的成员。论文主要探讨了一种新的多模态医学图像配准方法，利用信息论中的基本概念——互信息（Mutual Information, MI）或相对熵，作为图像配准的新匹配标准。互信息是一种度量两个随机变量之间相互依赖程度的指标，它在统计上衡量了两个图像对应体素强度之间的信息冗余。在几何对齐的理想情况下，如果两幅图像匹配，这种冗余通常达到最大值。该方法的优点在于，它不假设这种依赖关系的性质，并且不对涉及的模态图像内容施加任何限制性约束，因此具有广泛的适用性和强大的配准能力。论文通过与立体定向注册的比较，验证了互信息准则在刚体配准中的准确性。具体实验涵盖了计算机断层扫描（CT）、磁共振成像（MRI）以及正电子发射断层扫描（PET）图像的配准。这种方法的准确性和有效性通过实际数据进行了验证，证明了其在解决多模态医学图像配准问题上的潜力。在医学图像处理领域，配准是关键步骤之一，因为它允许不同成像技术的数据融合，从而提供更全面的解剖结构或生理功能信息。例如，CT图像可以提供良好的解剖结构细节，而MRI则擅长显示软组织对比，PET则能反映生物代谢活动。通过互信息最大化的配准，这些不同模态的图像可以有效地结合，提升诊断和治疗决策的精度。论文进一步可能讨论了计算互信息的算法实现，以及优化过程以找到最佳配准参数。此外，可能还包含了对不同图像配准技术的比较，以及对配准误差的分析和评估方法。这种方法的创新性在于引入了一个通用的、不受特定图像特征限制的配准准则，为多模态医学图像分析开辟了新的路径。

MAES et al.: MULTIMODALITY IMAGE REGISTRATION BY MAXIMIZATION OF MUTUAL INFORMATION 189

(a) (b)

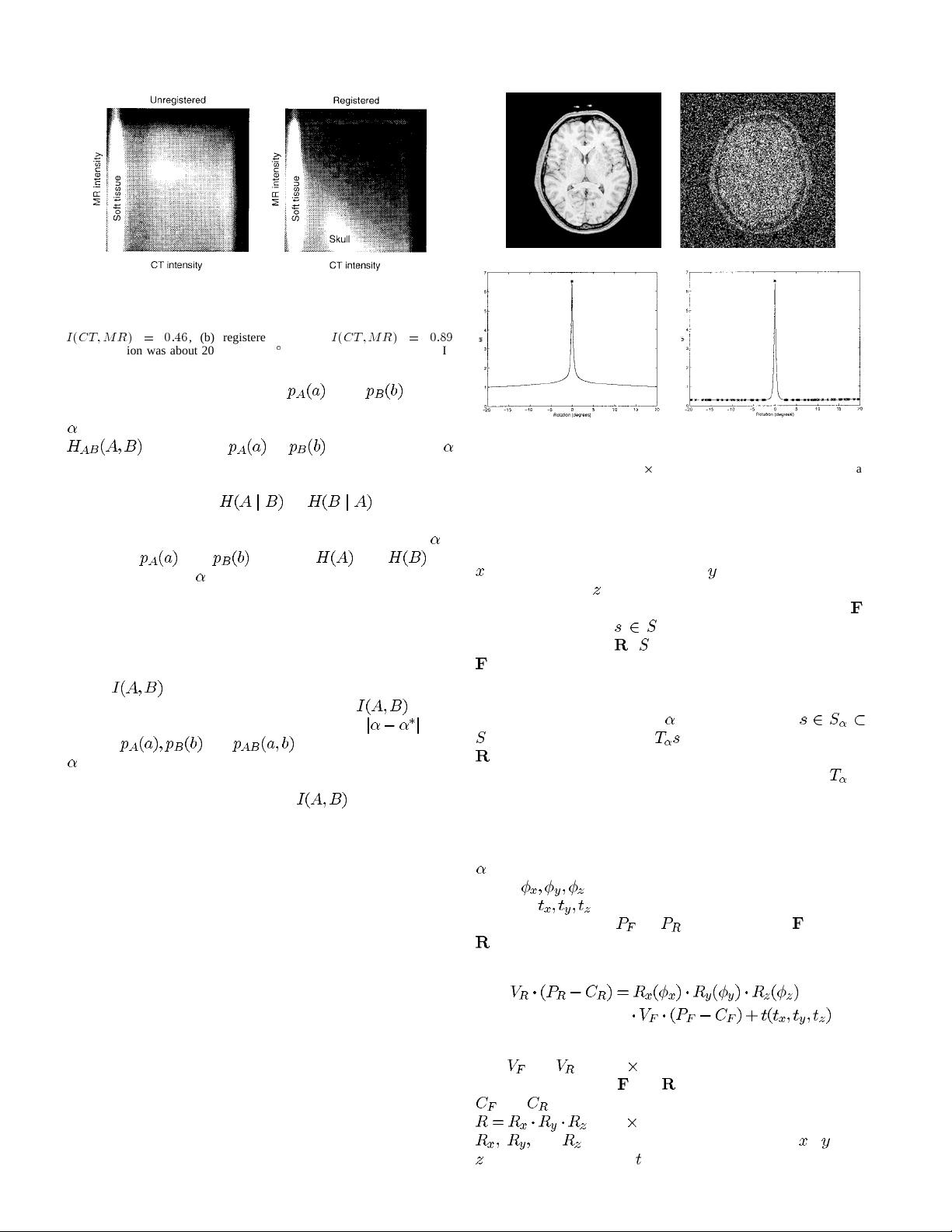
Fig. 1. Joint histogram of the overlapping volume of the CT and MR

brain images of dataset A in Tables II and III: (a) Initial position:

(

CT; MR

)=0

, (b) registered position:

(

CT;M R

)=0

Misregistration was about 20 mm and 10



(see the parameters in Table III).

If both marginal distributions and can be

considered to be independent of the registration parameters

, the MI criterion reduces to minimizing the joint entropy

[6]. If either or is independent of ,

which is the case if one of the images is always completely

contained in the other, the MI criterion reduces to minimizing

the conditional entropy

or . However, if

both images only partially overlap, which is very likely during

optimization, the volume of overlap will change when

varied and

and and also and will

generally depend on

. The MI criterion takes this into account

explicitly, as becomes clear in (2), which can be interpreted

as follows [27]: “maximizing MI will tend to ﬁnd as much

as possible of the complexity that is in the separate datasets

(maximizing the ﬁrst two terms) so that at the same time they

explain each other well (minimizing the last term).”

For

to be useful as a registration criterion and

well behaved with respect to optimization,

should

vary smoothly as a function of misregistration

. This

requires

and to change smoothly when

is varied, which will be the case if the image intensity

values are spatially correlated. This is illustrated by the graphs

in Fig. 2, showing the behavior of

as a function of

misregistration between an image and itself rotated around the

image center. The trace on the left is obtained from an original

MR image and shows a single sharp optimum with a rather

broad attraction basin. The trace on the right is obtained from

the same image after having reduced the spatial correlation of

the image intensity by repeatedly swapping pairs of randomly

selected pixels. This curve shows many local maxima and

the attraction basin of the global maximum is also much

smaller, which deteriorates the optimization robustness. Thus,

although the formulation of the MI criterion suggests that

spatial dependence of image intensity values is not taken into

account, such dependence is in fact essential for the criterion

to be well behaved around the registration solution.

III. A

LGORITHM

A. Transformation

Each of the images is associated an image coordinate frame

with its origin positioned in a corner of the image, with the

(a) (b)

Fig. 2. Spatial correlation of image intensity values increases MI registration

robustness. Top: (a) original 256

256 2-D MR image and (b) image of (a)

shufﬂed by swapping 30 000 randomly selected pixel pairs. Both images have

the same image content. Bottom: MI registration traces obtained using partial

volume distribution (PV) interpolation for in-plane rotation of each image

over itself. Local maxima are marked with “*”.

axis along the row direction, the axis along the column

direction, and the

axis along the plane direction.

One of the images is selected to be the ﬂoating image,

from which samples

are taken and transformed into

the reference image,

. can be the set of grid points of

or a sub- or superset thereof. Subsampling of the ﬂoating

image might be used to increase speed performance, while

supersampling aims at increasing accuracy. For each value

of the registration parameter

only those values

are retained for which falls inside the volume of

In this paper, we have restricted the transformation

rigid-body transformations only, although it is clear that the

MI criterion can be applied to more general transformations as

well. The rigid-body transformation is a superposition of a 3-

D rotation and a 3-D translation and the registration parameter

is a six-component vector consisting of three rotation

angles

(measured in degrees) and three translation

distances

(measured in millimeters). Transformation

of image coordinates

to from the image to image

is given by

(8)

with

and being 3 3 diagonal matrixes representing the

voxel sizes of images

and , respectively (in millimeters),

and the image coordinates of the centers of the images,

the 3 3 rotation matrix, with the matrixes

and representing rotations around the -, -, and

-axis, respectively, and the translation vector.

剩余11页未读，继续阅读

weixin_39840588

粉丝: 451
资源: 1万+

利用互信息最大化进行多模态医学图像配准

C++Primer 第4版-习题解答(完整版)+源码

maes_que_codam

MAES_CORE_SYSTEM_SERVER

基于圆的眼中心定位（CECL）：https://www.researchgate.net/publication/277143494_Circle-based_Eye_Center_Localization_(CECL)-matlab开发

maes3-开源

neo_信用卡欺诈预测模型.pdf

多智能体系统文献综述.pdf

基于深度学习的环境声音识别.pdf

基于Matlab的异步电机间接定子量仿真研究.pdf

最新资源