线性代数方程组数值解法:直接法与迭代法MATLAB实现
版权申诉
"这篇文档是关于线性代数方程组数值解法的综述,特别提到了MATLAB的实现。作者讨论了数值计算在科学技术中的重要性,并将线性代数方程组的解法分为直接法和迭代法。直接法主要包括高斯消元法和矩阵三角分解法,而迭代法则涉及Jacobi法、SOR法和SSOR法。文档详细阐述了高斯消元法的步骤和条件,强调了在计算过程中避免主元为零的重要性。"
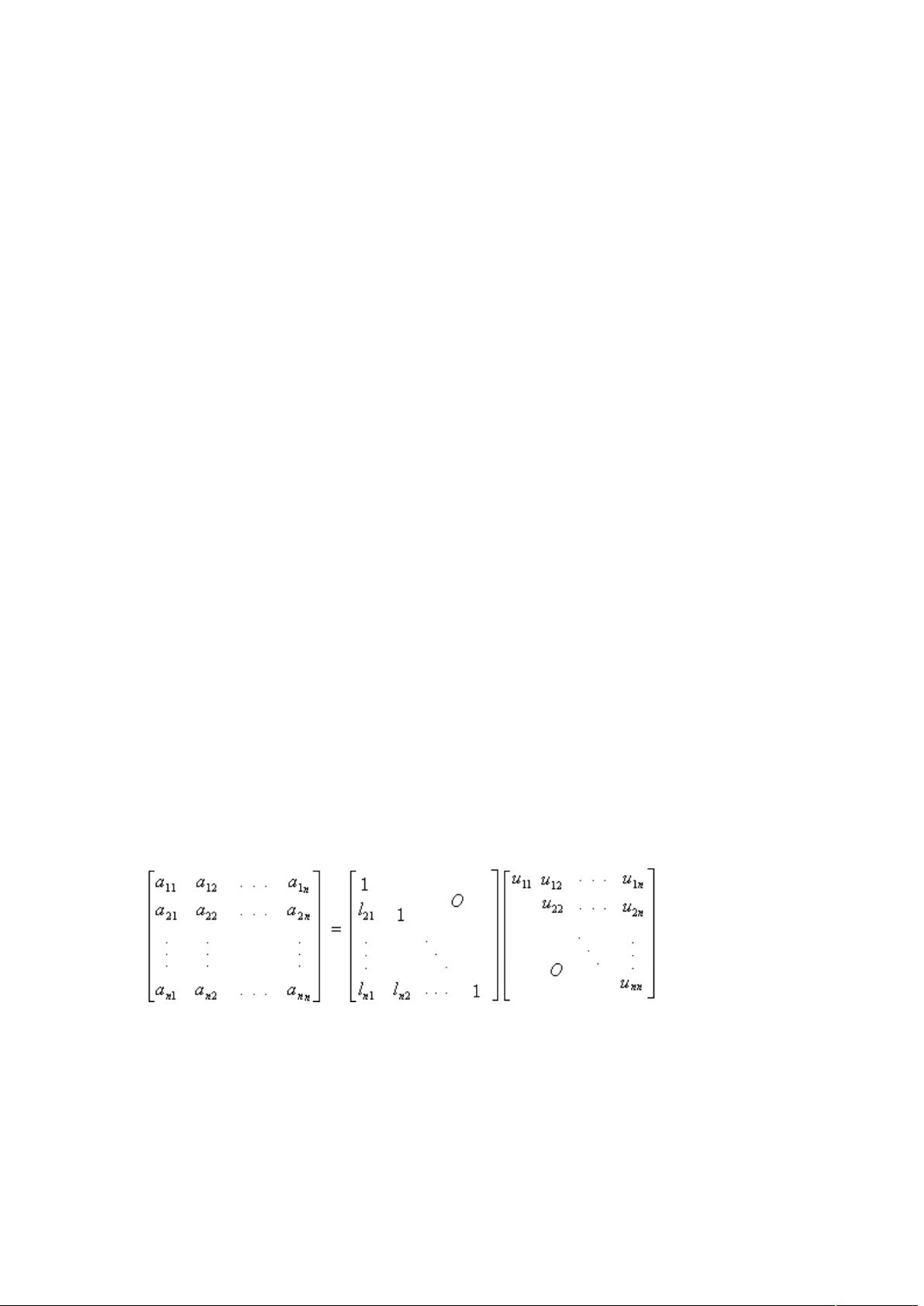
在数值计算领域,线性代数方程组的求解是核心问题,特别是在解决工程技术问题时。直接法和迭代法是解决这类问题的两种主要策略。直接法如高斯消元法,通过一系列行操作将矩阵转化为上三角形,然后回代求解。高斯消元法的关键在于避免主元为零,以确保解的存在性和稳定性。然而,对于大规模稀疏矩阵,直接法可能不适用,这时迭代法就显得更为有效。
迭代法,例如Jacobi法、SOR法(松弛法)和SSOR法,它们通过不断迭代接近方程组的精确解。这些方法在处理大型稀疏矩阵时更具优势,因为它们需要的存储空间较少,且原系数矩阵保持不变。然而,迭代法的收敛性和速度是需要考虑的关键因素,这可能影响解的质量和计算时间。
在MATLAB中,有内置的函数支持这两种方法,使得线性代数方程组的数值解变得容易。MATLAB提供了高效的线性代数运算工具,可以便捷地实现直接法和迭代法,对于教学和科研工作来说,是非常强大的辅助工具。
对于实际应用,例如在微分方程的离散化问题中,通常会生成大型的线性代数方程组,这时选择合适的解法至关重要。如果方程组规模较小,且矩阵密集,直接法可能是首选。相反,如果方程组规模大且稀疏,迭代法更合适。在实际操作中,还需要根据问题的具体特性调整算法参数,以达到最佳解算效果。
理解线性代数方程组的数值解法及其MATLAB实现对于任何涉及数值计算的领域都是基础且重要的。无论是直接法还是迭代法,选择正确的方法并合理实施,能够高效解决复杂的问题,为科学研究和技术发展提供有力的支持。
2021-09-28 上传
2022-07-04 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
104 浏览量
omyligaga
- 粉丝: 100
最新资源
- 打造仿天天动听的自定义上拉歌词控件教程
- 新型建筑物绝缘隔震体系技术文件发布
- Android开发进阶:UI、存储、网络与AppWidget全面实践
- x86平台Qtopia软件包安装指南
- FOSSASIA峰会2010活动站点解析与HTML技术应用
- Java编程思想课后习题答案解析
- C语言实现高效素数筛选工具——线性筛法
- Bootstrap前端模板开发指南与资源文件解析
- C++实现的初学者学生选课系统介绍
- FiveM资源开发基础样板:mx-speedometer
- Android应用连接WebService的实现方法
- Odin3 v3.07 cn中文版:手机刷机恢复神器
- 如何下载并安装Maven 3.8版本
- 建筑楼房拆除自动化:混凝土墙体自动打钻切割设备
- C#实现多页PDF转图片的第三方库介绍
- 学成在线静态网站开发实战案例