x =4= 3 3 + 2 = 5. So chapter is assigned the label “0.5”. Note that extended Dewey labels maintain the order of children under
the book. Our function for label generation explicitly considers the order of sibling nodes.
We show space complexity of extended Dewey using the following theorem.
Theorem 3.2. The extended Dewey does not alter the asymptotic space complexity of the original Dewey labeling scheme.
Proof. According to the formula in (2.2), it is not hard to prove that given any element s, the gap between the last components of
the labels for every two neighboring elements under s is no more than |CT(t
s
)|. Hence, with the binary representation of integers,
the length of each component i of extended Dewey label is at most log
2
|CT(t
s
i
)| more than that of the original Dewey. Therefore,
the length difference between an extended Dewey label with m components and an original one is at most ∑
i =1
m
log
2
|CT(t
s
i
)|.
Since m and |CT(t
s
i
)| are small, it is reasonable to consider this difference is a small constant. As a result, the extended Dewey does
not alter asymptotic space complexity of the original Dewey. □
3.2. Finite state transducer
Given the extended Dewey label of any element, we can use a finite state transducer (FST) to convert this label into the sequence
of element names which reveals the whole path from the root to this element. We begin this section by presenting a function F(t, x)
which will be used to define FST.
Definition 3.3. (Function F(t,x)) Let Z denotes the non-negative integer set and Σ denotes the alphabet of all distinct tags in an
XML document T. Given an tag t in T, suppose CT(t)={t
0
,t
1
,⋯,t
n − 1
}, a function F(t,x): Σ × Z → Σ can be defined by F(t,x)=t
k
, where
k=x mod n.
Definition 3.4. (Finite State Transducer) Given child names clues and an extended Dewey label, we can use a deterministic finite
state transducer (FST) to translate the label into a sequence of element names. FST is a 5-tuple (I, S, i, δ, and o), where (i) the input
set I=Z ∪ {−1}; (ii) the set of states S = Σ∪{PCDATA}, where PCDATA is a state to denote text value of an element; (iii) the initial
state i is the tag of the root in the document; (iv) the state transition function δ is defined as follows. For ∀ t ∈ Σ,ifx=−1, δ(t, x)=
PCDATA, otherwise δ(t, x)=F(t, x). No other transition is accepted. (v) The output value o is the current state name.
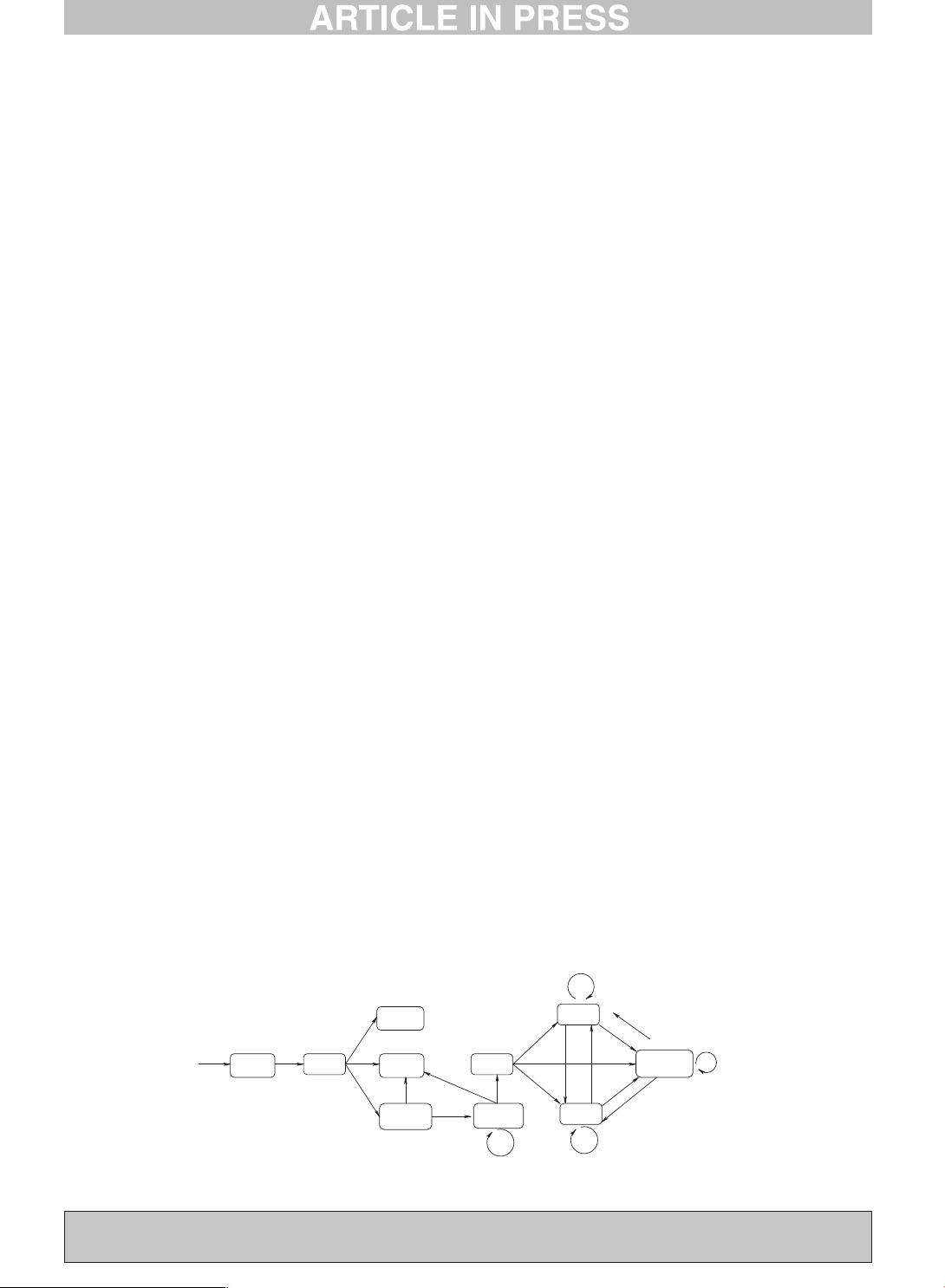
Example 3.5. Fig. 4 shows the FST for DTD in Fig 3. For clarity, we do not explicitly show the state for PCDATA here. An input of −1
from any state will transit to the terminating state PCDATA. This FST can convert any extended Dewey label to an element path. For
instance, given an extended Dewey label “0.5.1.1”, using the above FST, we derive that its path is “bib/book/chapter/section/text”.
It is worth noting three points about FST:(i) the memory size of the above FST is quadratic in the number of distinct tags in XML
documents, as the number of transition in FST is quadratic in the worst case; and (ii) we allow recursive element names in a
document path, which is demonstrated as a loop in FST; and (iii) the time complexity of FST is linear in the length of an extended
Dewey label, but independent of the complexity of schema definition.
3.3. Dynamic XML labeling
We next discuss how to support updates in XML documents based on extended Dewey labeling scheme. One way is to use
ORDPATH [32], where odd numbers are used to represent the order coding and even numbers are reserved for delimiters.
Assuming a DTD is a → (b|c)
, for instance, considering an XML document with the root a
1
that has three children b
1
, c
1
and c
2
, their
respective extended Dewey labels are assigned 1, 2 and 4 (a
1
is labeled ε), and dynamic extended Dewey labels should be assigned
1, 3 and 7 instead. If a new element b
2
is inserted between c
1
and c
2
, then it could be elegantly assigned 3.4.1 without updating any
mod 3=0
bib
book
author
section
emph
keyword
title
chapter
bold
text
mod 1=0
mod 3=0
mod 3=1
mod 3=2
mod 2=1
mod 3=1
mod 3=2
mod 2=0
mod 3=0
mod 3=1
mod 3=2
mod 3=2
mod 3=2
mod 3=2
mod 3=0
mod 3=2
mod 3=0
mod 3 =1
mod 3=0
mod 3=1
Fig. 4. A sample FST for DTD in Fig 3.
5J. Lu et al. / Data & Knowledge Engineering xxx (2010) xxx–xxx
Please cite this article as: J. Lu, et al., Indexing and querying XML using extended Dewey labeling scheme, Data Knowl. Eng.
(2010), doi:10.1016/j.datak.2010.08.001









