1668 IEEE COMMUNICATIONS LETTERS, VOL. 16, NO. 10, OCTOBER 2012
CRC-Aided Decoding of Polar Codes
Kai Niu and Kai Chen
Abstract—CRC (cyclic redundancy check)-aided decoding
schemes are proposed to improve the performance of polar
codes. A unified description of successive cancellation decoding
and its improved version with list or stack is provided and
the CRC-aided successive cancellation list/stack (CA-SCL/SCS)
decoding schemes are proposed. Simulation results in binary-
input additive white Gaussian noise channel (BI-AWGNC) show
that CA-SCL/SCS can provide significant gain of 0.5 dB over
the turbo codes used in 3GPP standard with code rate 1/2 and
code length 1024 at the block error probability (BLER) of 10
−4
.
Moreover, the time complexity of CA-SCS decoder is much lower
than that of turbo decoder and can be close to that of successive
cancellation (SC) decoder in the high SNR regime.
Index Terms—Polar codes, CRC, successive cancellation de-
coding, stack decoding, list decoding.
I. INTRODUCTION
P
OLAR codes, proposed by Arıkan [1], [2], are proved
to achieve the symmetric capacity of the binary-input
discrete memoryless channels (B-DMCs) under a successive
cancellation (SC) decoder. However, the finite-length per-
formance is unsatisfying. So it has stirred great passions
to find more powerful decoding methods to improve the
performance of polar codes. Belief propagation (BP) [3], [4]
and linear programming (LP) [5] decoders are reported to
have a significant improvement over SC. Later, successive
cancellation list (SCL) [6], [9] and successive cancellation
stack (SCS) [10] decoders are introduced to approach the
performance of maximum likelihood (ML) decoder with an
acceptable complexity. The enhancement of SC using a list
(or a stack) has essentially the same idea with the recursive
decoding applied to RM codes [11] ([12]).
Cyclic redundancy check (CRC) codes are the most widely
used for error-detecting in practical communications systems,
e.g. 3rd generation partnership project (3GPP) standard [15]. A
K-bit input block of the error-correcting encoder consists of k
information bits an d an m-bit CRC sequence, i.e. K = k +m.
By viewing the CRC bits as part of source bits for the error-
correcting code, the code ra te is still defined as R = K/N.In
this paper, we propose a combination of SCL (SCS) decoder
and CRC detector to further improve the performance of polar
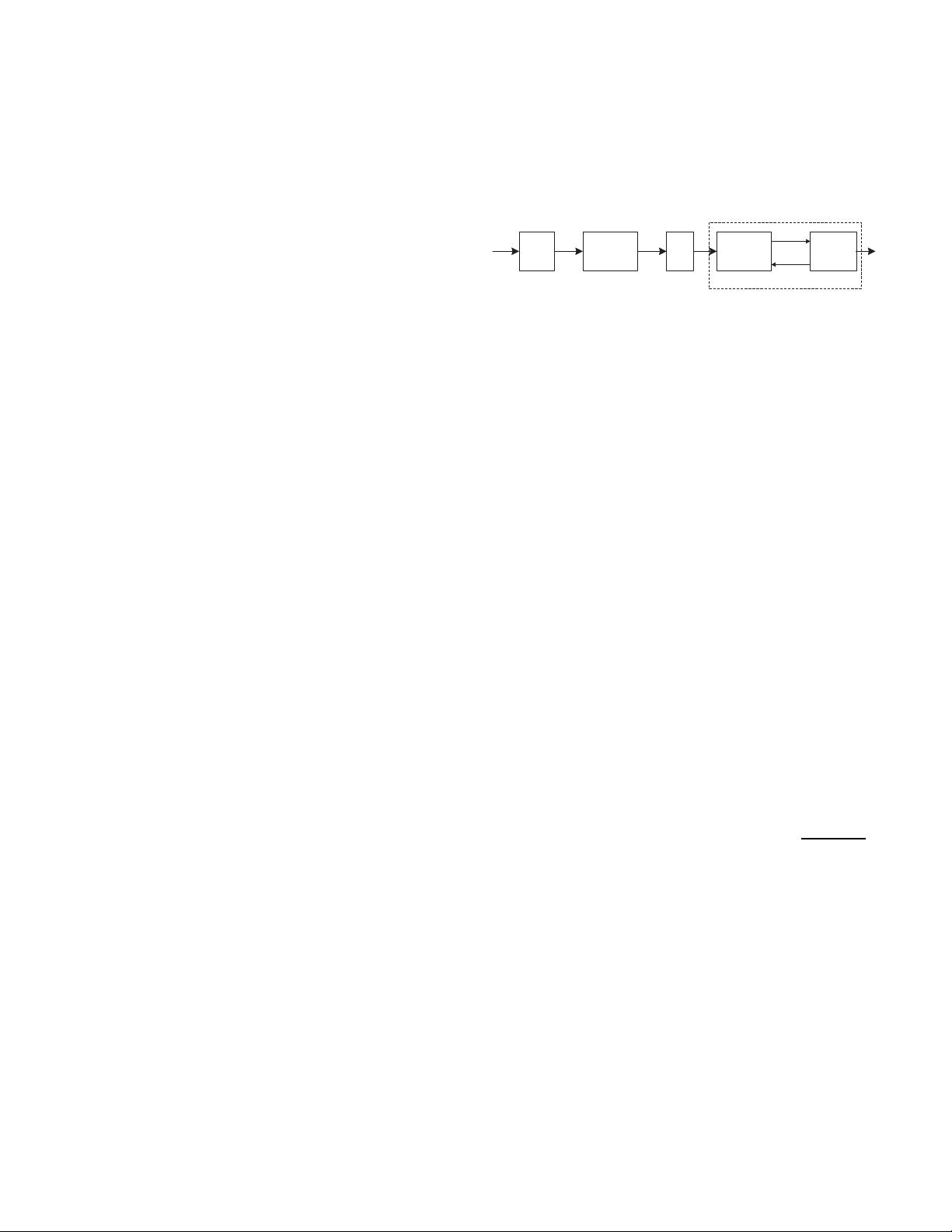
codes. As shown in Fig. 1, at the receiver, the SCL (SCS)
decoder outputs the candidate sequences into CRC detector
and the latter feeds the check results back to help the codeword
Manuscript received July 6, 2012. The associate editor coordinating the
review of this letter and approving it for publication was A. Burr.
This work was supported by the National Natural Science Foundation of
China (No. 61171099), the National Basic Research Program of China (973
Program) (No. 2009CB320401), and Qualcomm Corporation.
The authors are with the Ke y Laboratory of Universal Wireless Communi-
cation, Ministry of Education, Beijing University of Posts and Telecommuni-
cations, Beijing 100876, China (e-mail: {niukai, kaichen}@bupt.edu.cn).
Digital Object Identifier 10.1109/LCOMM.2012.090312.121501
candidate
sequences
k
bits
Kkm
bits
N
bits
CRC
Polar
Encoder
SCL/SCS
W
DeCRC
CA-SCL/SCS decoder
check
results
Fig. 1. polar coding and CRC-aided decoding schemes.
determination. We refer to such a decoding scheme as CRC-
aided SCL/SCS (CA-SCL/SCS). The performance of CA-
SCL/SCS is substantially improved and even outperforms that
of turbo codes. In a recent paper [7], Tal and Vardy indepen-
dently formulate the similar statement on CRC-concatenated
polar coding scheme based on SCL decoding. We note at this
point that this idea was also mentioned in the presentation by
Tal and Vardy and th e p lenary talk by Arıkan (credited to Tal
and Vardy) at ISIT 2011.
The remainder of the paper is organized as follows. Section
II describes the preliminaries of polar coding and gives a
unified description of SC, SCL and SCS decoding by a
posteriori probability (APP). Then the CRC-aided decoding
algorithms are addressed in Section III. Section IV p rovides
the simulation results for CA-SCL/SCS and turbo codes and
presents the decoding comp lexity comparison. Finally, Section
V concludes the paper.
II. P
RELIMINARIES
A. Notations and the A Posteriori Probability
We use the same notations defined in [1]. Assuming the
communication over a B-DMC W : X→Y,whereX and
Y denote input and output alphabet respectively, the channel
transition probabilities are defined as W (y |x ), x ∈X, y ∈Y
and x is uniformly distributed in X , thus the channel a pos-
teriori probabilities can be written as P (x |y )=
W (y|x )
v
W (y|v )
.
After channel combining and splitting oper ation on N =2
n
independent uses of W ,wegetN successive uses of syn-
thesized binary input channels W
(i)
N
with i =1, 2, ··· ,N.
The information bits can be assigned to the channels with
indices in the info rmation set A, which are the more reliable
subchannels. The complementary set A
c
denotes the frozen
bit set and the frozen bits u
A
c
can be set to fixed bit values,
such as all zeros, for the symmetric channels.
To put it another way, polar coding is performed on the
constraint x
N
1
= u
N
1
G
N
,whereG
N
is the generato r matrix
and u
N
1
,x
N
1
∈{0, 1}
N
are the source and code block respec-
tively. The source block u
N
1
consists of information bits u
A
and frozen bits u
A
c
. The generator matrix can be recursively
defined as G
N
= R
N
F ⊗ G
N/2
, G
2
= F =
10
11
,
where ⊗ denotes the Kronecker product and R
N
is the reverse
shuffle matrix.
1089-7798/12$31.00
c
2012 IEEE









