二叉树遍历算法详解：递归与非递归实现

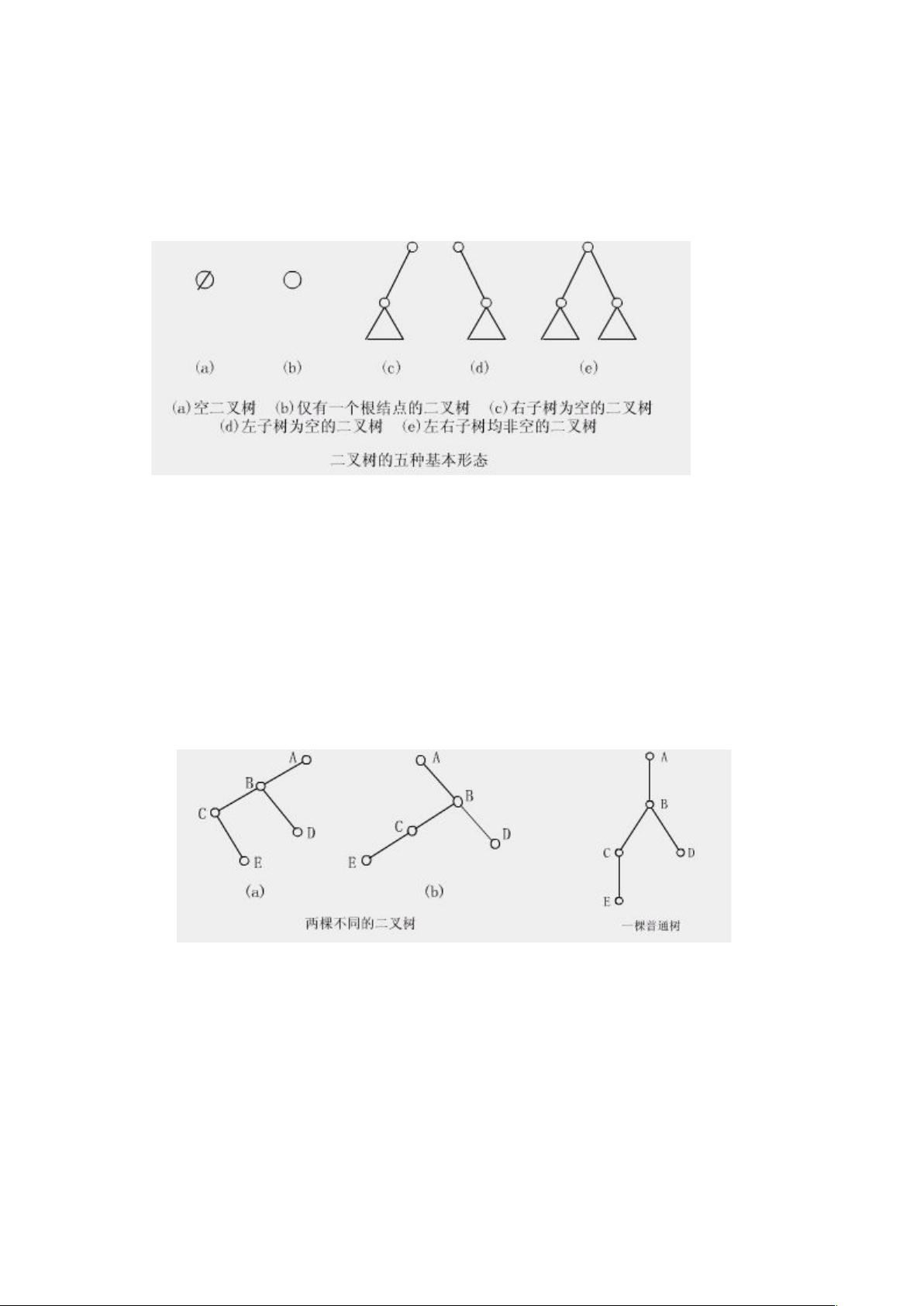
"这篇文档是关于二叉树遍历的课程设计报告，涵盖了二叉树的各种遍历方法，包括递归和非递归的前序、中序、后序遍历，以及层序遍历。报告旨在提升学生的编程能力和理论实践结合的能力。" 二叉树遍历是计算机科学中数据结构领域的一个重要概念，主要应用于树形数据结构的处理。在这个课程设计中，学生被要求实现和理解以下知识点： 1. **二叉树定义**：二叉树是由零个或多个节点组成的有限集合，每个节点可能有零个、一个或两个子节点，分为左子树和右子树。 2. **二叉树的形态**：二叉树有五种基本形态，包括空树、只有一个根节点、根节点只有左子树、根节点只有右子树，以及根节点同时拥有左右子树的情况。 3. **遍历方法**： - **前序遍历**（根-左-右）：首先访问根节点，然后递归地访问左子树，最后访问右子树。 - **中序遍历**（左-根-右）：首先递归地访问左子树，然后访问根节点，最后访问右子树。在二叉搜索树中，中序遍历会得到升序序列。 - **后序遍历**（左-右-根）：首先递归地访问左子树，然后访问右子树，最后访问根节点。 - **层序遍历**（广度优先搜索）：使用队列，从根节点开始，逐层访问每个节点，每层从左到右。 4. **递归遍历**：通过函数调用自身实现遍历，简单但可能导致调用栈过深的问题。 5. **非递归遍历**：通常使用辅助数据结构如栈或队列来实现，避免了递归带来的栈空间限制，例如，前序遍历可以使用栈，后序遍历可以使用两个栈或者一个栈加一个临时变量。 6. **设计过程**：设计报告要求学生从问题分析、程序模块编写、关键函数解释、程序调试到报告撰写，全方位锻炼编程和解决问题的能力。 7. **应用**：遍历二叉树的方法广泛应用于数据结构的实现，如查找、排序、树的复制、打印等操作。 8. **技能提升**：通过这个设计，学生不仅可以掌握二叉树遍历的算法，还能增强C/C++编程技巧，提高调试和测试程序的能力，以及写作和表达能力。 这个课程设计是全面理解和熟练应用二叉树遍历算法的重要实践，对于计算机科学的学习者来说，这是一个宝贵的锻炼机会，有助于他们建立坚实的理论基础和实践经验。