全等三角形解题模型探索：等腰直角与30°-60°三角形

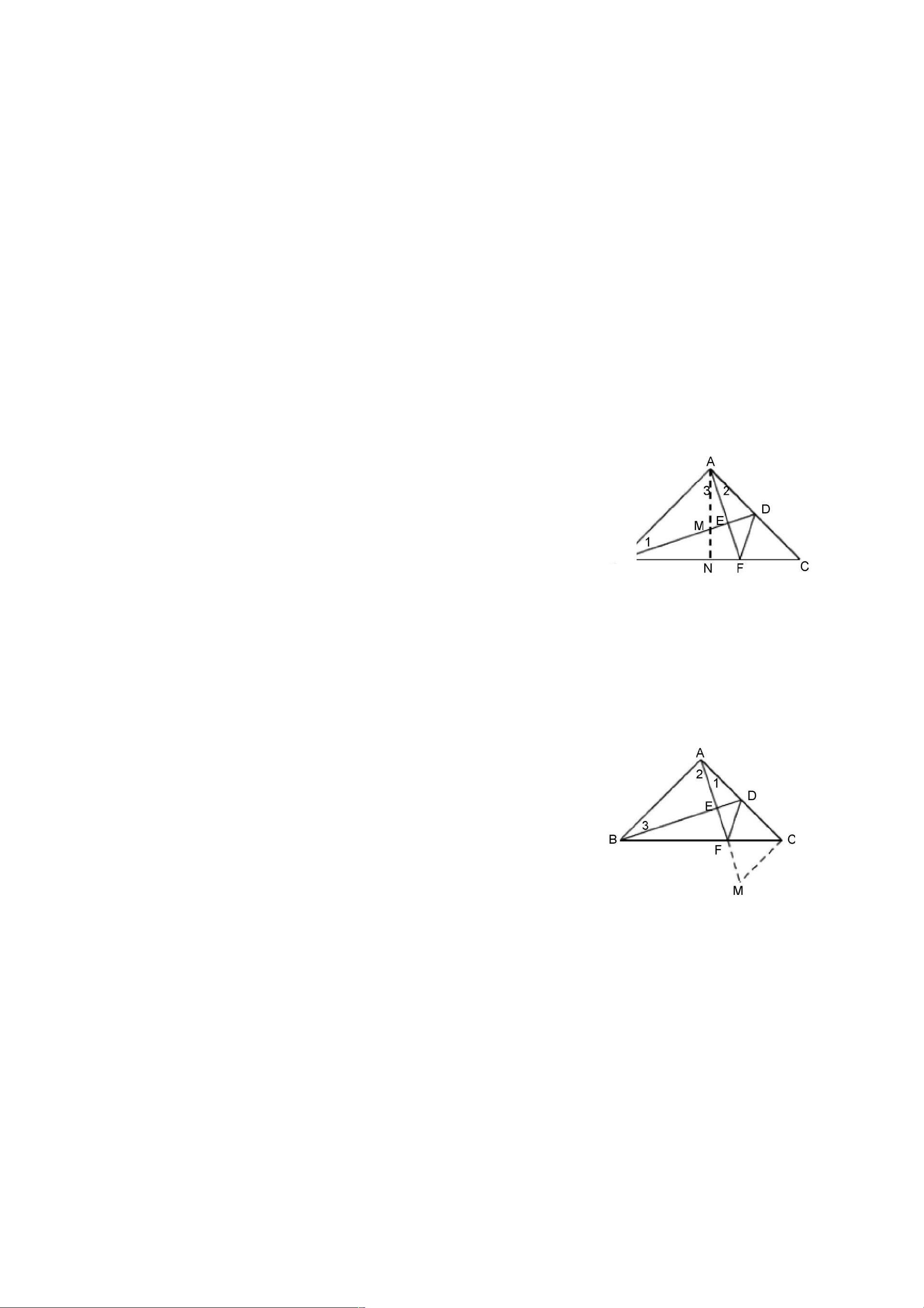
"该文档是关于全等三角形学习的资料，主要讲解了等腰直角三角形和含30°、60°角的三角形的经典模型，并提供了例题及解析，帮助学生掌握全等三角形的证明方法。" 在几何学中，全等三角形是指两个三角形在形状和大小上完全相同，它们的对应边和对应角相等。了解和掌握全等三角形的经典模型对于解决几何问题至关重要。文档中提到了两种常见的模型： 1. **等腰直角三角形模型**： - **思路一**：利用等腰直角三角形的特性，如AC=BC，∠ACB=90°，45°角等，可以直接得出某些边角关系。 - **思路二**：常通过作高线来利用三线合一的性质，例如在直角顶点处的高同时是中线和角平分线，有助于简化问题。 例如在【例1】中，通过分析等腰直角三角形Rt△ABC，可以发现OA=OB=OC，进而证明无论点MN如何移动，只要保持AN=CM，AOM始终是等腰直角三角形。通过连结OA，利用等腰直角三角形的性质，可以一步步推导出结论。 2. **含30°、60°角的三角形模型**： - 这种模型通常涉及到特殊比例的边，如30°-60°-90°三角形的两边之比为1:√3，以及与等腰直角三角形的关联。 在【例2】中，两个全等的含30°、60°角的三角板ADE和ABC，通过证明△EDM与△CAM全等，可以得出△EMC是等腰直角三角形，因为它们的两边和一个角对应相等。 文档还提供了两种不同的证明方法来解决特定问题，如在证明AD=BC+DF时，可以分别通过构造全等三角形ABM与CAF或ACM与BAD来达到目的。 通过这些经典模型的学习，学生可以更熟练地运用全等三角形的性质和判定定理，例如SAS、ASA、SSS、AAS等，解决复杂的几何问题。在实际解题过程中，灵活运用辅助线和已知条件，结合图形推理，是解决问题的关键。这样的训练有助于提升学生的逻辑思维能力和空间想象能力。