程序员必读：理解内存与CPU缓存优化的实战指南

需积分: 50 142 浏览量更新于2024-07-16 收藏 1006KB PDF 举报

"《每个程序员都应该了解的内存知识》是 Ulrich Drepper 的经典之作，他作为 Red Hat 公司的工程师，且曾是 Glibc 的核心开发者，这篇文章深入浅出地探讨了现代计算机内存系统的原理与优化。随着CPU核心性能的提升和数量增多，内存访问成为了许多程序的瓶颈。硬件设计者开发了诸如CPU缓存这样的高级技术来提升效率，但这些技术的有效运用离不开程序员的理解与配合。首先，文章介绍了RAM/DRAM硬件的基本原理，解释了内存如何存储和检索数据，以及这些硬件在计算机系统中的作用。作者强调了早期计算机设计中各个组件（如CPU、内存、硬盘和网络接口）之间的相对平衡，但在现代复杂系统中，这种平衡已经不再适用。其次，文章详细阐述了CPU的多级缓存（Cache）机制。CPU缓存旨在减少对主内存（RAM）的频繁访问，通过将常用数据复制到靠近处理器的高速存储区域，从而显著提高程序运行速度。它的工作原理包括一级缓存（L1）、二级缓存（L2）和有时存在的三级缓存（L3），程序员需要理解如何利用这些缓存层次结构来优化代码，避免缓存未命中的开销。此外，DMA（Direct Memory Access）原理也在文中得到了讲解。DMA技术允许外部设备（如硬盘）直接与内存交换数据，无需经过CPU处理，这对于提高I/O操作性能至关重要。了解何时使用DMA以及如何正确配置，可以避免CPU资源浪费，进一步提升程序整体效能。最后，作者针对NUMA（Non-Uniform Memory Access）架构进行了讨论。在现代多核和多处理器系统中，内存访问速度受到节点间物理距离的影响。了解NUMA模型有助于编写能够充分利用局部内存和减少跨节点通信的高效代码。《每个程序员都应该了解的内存知识》是一份实用的指南，它不仅解释了硬件的基础，还提供了如何通过编程策略实现内存优化和系统性能提升的关键见解。对于想要深入理解计算机底层机制和追求高性能程序设计的程序员来说，这篇文章是不可或缺的学习资料。"

as the offset into the cache line. The next S bits select

the “cache set”. We will go into more detail soon on

why sets, and not single slots, are used for cache lines.

For now it is sufﬁcient to understand there are 2

sets of

cache lines. This leaves the top 32−S−O = T bits which

form the tag. These T bits are the value associated with

each cache line to distinguish all the aliases

which are

cached in the same cache set. The S bits used to address

the cache set do not have to be stored since they are the

same for all cache lines in the same set.

When an instruction modiﬁes memory the processor still

has to load a cache line ﬁrst because no instruction mod-

iﬁes an entire cache line at once (exception to the rule:

write-combining as explained in section 6.1). The con-

tent of the cache line before the write operation therefore

has to be loaded. It is not possible for a cache to hold

partial cache lines. A cache line which has been written

to and which has not been written back to main memory

is said to be “dirty”. Once it is written the dirty ﬂag is

cleared.

To be able to load new data in a cache it is almost always

ﬁrst necessary to make room in the cache. An eviction

from L1d pushes the cache line down into L2 (which

uses the same cache line size). This of course means

room has to be made in L2. This in turn might push the

content into L3 and ultimately into main memory. Each

eviction is progressively more expensive. What is de-

scribed here is the model for an exclusive cache as is

preferred by modern AMD and VIA processors. Intel

implements inclusive caches

where each cache line in

L1d is also present in L2. Therefore evicting from L1d is

much faster. With enough L2 cache the disadvantage of

wasting memory for content held in two places is mini-

mal and it pays off when evicting. A possible advantage

of an exclusive cache is that loading a new cache line

only has to touch the L1d and not the L2, which could be

faster.

The CPUs are allowed to manage the caches as they like

as long as the memory model deﬁned for the processor

architecture is not changed. It is, for instance, perfectly

ﬁne for a processor to take advantage of little or no mem-

ory bus activity and proactively write dirty cache lines

back to main memory. The wide variety of cache archi-

tectures among the processors for the x86 and x86-64,

between manufacturers and even within the models of

the same manufacturer, are testament to the power of the

memory model abstraction.

In symmetric multi-processor (SMP) systems the caches

of the CPUs cannot work independently from each other.

All processors are supposed to see the same memory con-

tent at all times. The maintenance of this uniform view

of memory is called “cache coherency”. If a processor

were to look simply at its own caches and main mem-

All cache lines with the same S part of the address are known by

the same alias.

This generalization is not completely correct. A few caches are

exclusive and some inclusive caches have exclusive cache properties.

ory it would not see the content of dirty cache lines in

other processors. Providing direct access to the caches

of one processor from another processor would be terri-

bly expensive and a huge bottleneck. Instead, processors

detect when another processor wants to read or write to a

certain cache line.

If a write access is detected and the processor has a clean

copy of the cache line in its cache, this cache line is

marked invalid. Future references will require the cache

line to be reloaded. Note that a read access on another

CPU does not necessitate an invalidation, multiple clean

copies can very well be kept around.

More sophisticated cache implementations allow another

possibility to happen. Assume a cache line is dirty in

one processor’s cache and a second processor wants to

read or write that cache line. In this case the main mem-

ory is out-of-date and the requesting processor must, in-

stead, get the cache line content from the ﬁrst proces-

sor. Through snooping, the ﬁrst processor notices this

situation and automatically sends the requesting proces-

sor the data. This action bypasses main memory, though

in some implementations the memory controller is sup-

posed to notice this direct transfer and store the updated

cache line content in main memory. If the access is for

writing the ﬁrst processor then invalidates its copy of the

local cache line.

Over time a number of cache coherency protocols have

been developed. The most important is MESI, which we

will introduce in section 3.3.4. The outcome of all this

can be summarized in a few simple rules:

• A dirty cache line is not present in any other pro-

cessor’s cache.

• Clean copies of the same cache line can reside in

arbitrarily many caches.

If these rules can be maintained, processors can use their

caches efﬁciently even in multi-processor systems. All

the processors need to do is to monitor each others’ write

accesses and compare the addresses with those in their

local caches. In the next section we will go into a few

more details about the implementation and especially the

costs.

Finally, we should at least give an impression of the costs

associated with cache hits and misses. These are the

numbers Intel lists for a Pentium M:

To Where Cycles

L1d ∼ 3

L2 ∼ 14

Main Memory ∼ 240

These are the actual access times measured in CPU cy-

cles. It is interesting to note that for the on-die L2 cache

16 Version 1.0 What Every Programmer Should Know About Memory

a large part (probably even the majority) of the access

time is caused by wire delays. This is a physical lim-

itation which can only get worse with increasing cache

sizes. Only process shrinking (for instance, going from

60nm for Merom to 45nm for Penryn in Intel’s lineup)

can improve those numbers.

The numbers in the table look high but, fortunately, the

entire cost does not have to be paid for each occurrence

of the cache load and miss. Some parts of the cost can

be hidden. Today’s processors all use internal pipelines

of different lengths where the instructions are decoded

and prepared for execution. Part of the preparation is

loading values from memory (or cache) if they are trans-

ferred to a register. If the memory load operation can

be started early enough in the pipeline, it may happen in

parallel with other operations and the entire cost of the

load might be hidden. This is often possible for L1d; for

some processors with long pipelines for L2 as well.

There are many obstacles to starting the memory read

early. It might be as simple as not having sufﬁcient re-

sources for the memory access or it might be that the ﬁnal

address of the load becomes available late as the result of

another instruction. In these cases the load costs cannot

be hidden (completely).

For write operations the CPU does not necessarily have

to wait until the value is safely stored in memory. As

long as the execution of the following instructions ap-

pears to have the same effect as if the value were stored

in memory there is nothing which prevents the CPU from

taking shortcuts. It can start executing the next instruc-

tion early. With the help of shadow registers which can

hold values no longer available in a regular register it is

even possible to change the value which is to be stored in

the incomplete write operation.

100

200

500

1000

Working Set Size (Bytes)

Cycles/Operation

Figure 3.4: Access Times for Random Writes

For an illustration of the effects of cache behavior see

Figure 3.4. We will talk about the program which gener-

ated the data later; it is a simple simulation of a program

which accesses a conﬁgurable amount of memory repeat-

edly in a random fashion. Each data item has a ﬁxed size.

The number of elements depends on the selected work-

ing set size. The Y–axis shows the average number of

CPU cycles it takes to process one element; note that the

scale for the Y–axis is logarithmic. The same applies in

all the diagrams of this kind to the X–axis. The size of

the working set is always shown in powers of two.

The graph shows three distinct plateaus. This is not sur-

prising: the speciﬁc processor has L1d and L2 caches,

but no L3. With some experience we can deduce that the

L1d is 2

bytes in size and that the L2 is 2

bytes in

size. If the entire working set ﬁts into the L1d the cycles

per operation on each element is below 10. Once the L1d

size is exceeded the processor has to load data from L2

and the average time springs up to around 28. Once the

L2 is not sufﬁcient anymore the times jump to 480 cycles

and more. This is when many or most operations have to

load data from main memory. And worse: since data is

being modiﬁed dirty cache lines have to be written back,

too.

This graph should give sufﬁcient motivation to look into

coding improvements which help improve cache usage.

We are not talking about a difference of a few measly per-

cent here; we are talking about orders-of-magnitude im-

provements which are sometimes possible. In section 6

we will discuss techniques which allow writing more ef-

ﬁcient code. The next section goes into more details of

CPU cache designs. The knowledge is good to have but

not necessary for the rest of the paper. So this section

could be skipped.

3.3 CPU Cache Implementation Details

Cache implementers have the problem that each cell in

the huge main memory potentially has to be cached. If

the working set of a program is large enough this means

there are many main memory locations which ﬁght for

each place in the cache. Previously it was noted that a

ratio of 1-to-1000 for cache versus main memory size is

not uncommon.

3.3.1 Associativity

It would be possible to implement a cache where each

cache line can hold a copy of any memory location (see

Figure 3.5). This is called a fully associative cache. To

access a cache line the processor core would have to

compare the tags of each and every cache line with the

tag for the requested address. The tag would be com-

prised of the entire part of the address which is not the

offset into the cache line (that means, S in the ﬁgure on

page 15 is zero).

There are caches which are implemented like this but,

by looking at the numbers for an L2 in use today, will

show that this is impractical. Given a 4MB cache with

64B cache lines the cache would have 65,536 entries.

To achieve adequate performance the cache logic would

have to be able to pick from all these entries the one

matching a given tag in just a few cycles. The effort to

Ulrich Drepper Version 1.0 17

Tag Data

Comp

Tag Offset

Figure 3.5: Fully Associative Cache Schematics

implement this would be enormous.

For each cache line a comparator is needed to compare

the large tag (note, S is zero). The letter next to each

connection indicates the width in bits. If none is given

it is a single bit line. Each comparator has to compare

two T-bit-wide values. Then, based on the result, the ap-

propriate cache line content is selected and made avail-

able. This requires merging as many sets of O data lines

as there are cache buckets. The number of transistors

needed to implement a single comparator is large espe-

cially since it must work very fast. No iterative com-

parator is usable. The only way to save on the number

of comparators is to reduce the number of them by iter-

atively comparing the tags. This is not suitable for the

same reason that iterative comparators are not: it takes

too long.

Fully associative caches are practical for small caches

(for instance, the TLB caches on some Intel processors

are fully associative) but those caches are small, really

small. We are talking about a few dozen entries at most.

For L1i, L1d, and higher level caches a different ap-

proach is needed. What can be done is to restrict the

search. In the most extreme restriction each tag maps

to exactly one cache entry. The computation is simple:

given the 4MB/64B cache with 65,536 entries we can

directly address each entry by using bits 6 to 21 of the

address (16 bits). The low 6 bits are the index into the

cache line.

Tag

MUX

Comp

MUX

Data

S S

Tag Set Offset

Figure 3.6: Direct-Mapped Cache Schematics

Such a direct-mapped cache is fast and relatively easy

to implement as can be seen in Figure 3.6. It requires

exactly one comparator, one multiplexer (two in this di-

agram where tag and data are separated, but this is not

a hard requirement on the design), and some logic to

select only valid cache line content. The comparator is

complex due to the speed requirements but there is only

one of them now; as a result more effort can be spent

on making it fast. The real complexity in this approach

lies in the multiplexers. The number of transistors in a

simple multiplexer grows with O(log N), where N is the

number of cache lines. This is tolerable but might get

slow, in which case speed can be increased by spending

more real estate on transistors in the multiplexers to par-

allelize some of the work and to increase the speed. The

total number of transistors can grow slowly with a grow-

ing cache size which makes this solution very attractive.

But it has a drawback: it only works well if the addresses

used by the program are evenly distributed with respect

to the bits used for the direct mapping. If they are not,

and this is usually the case, some cache entries are heav-

ily used and therefore repeated evicted while others are

hardly used at all or remain empty.

· · ·

Tag

MUX

· · ·

Data

· · ·

MUX

· · ·

S S

Comp

Tag Set Offset

Figure 3.7: Set-Associative Cache Schematics

This problem can be solved by making the cache set as-

sociative. A set-associative cache combines the good

features of the full associative and direct-mapped caches

to largely avoid the weaknesses of those designs. Fig-

ure 3.7 shows the design of a set-associative cache. The

tag and data storage are divided into sets, one of which is

selected by the address of a cache line. This is similar to

the direct-mapped cache. But instead of only having one

element for each set value in the cache a small number

of values is cached for the same set value. The tags for

all the set members are compared in parallel, which is

similar to the functioning of the fully associative cache.

The result is a cache which is not easily defeated by

unfortunate–or deliberate–selection of addresses with the

same set numbers and at the same time the size of the

cache is not limited by the number of comparators which

can be implemented economically. If the cache grows it

is (in this ﬁgure) only the number of columns which in-

creases, not the number of rows. The number of rows

(and therefore comparators) only increases if the asso-

ciativity of the cache is increased. Today processors are

using associativity levels of up to 24 for L2 caches or

higher. L1 caches usually get by with 8 sets.

18 Version 1.0 What Every Programmer Should Know About Memory

L2 Associativity

Cache Direct 2 4 8

Size

CL=32 CL=64 CL=32 CL=64 CL=32 CL=64 CL=32 CL=64

512k 27,794,595 20,422,527 25,222,611 18,303,581 24,096,510 17,356,121 23,666,929 17,029,334

1M 19,007,315 13,903,854 16,566,738 12,127,174 15,537,500 11,436,705 15,162,895 11,233,896

2M 12,230,962 8,801,403 9,081,881 6,491,011 7,878,601 5,675,181 7,391,389 5,382,064

4M 7,749,986 5,427,836 4,736,187 3,159,507 3,788,122 2,418,898 3,430,713 2,125,103

8M 4,731,904 3,209,693 2,690,498 1,602,957 2,207,655 1,228,190 2,111,075 1,155,847

16M 2,620,587 1,528,592 1,958,293 1,089,580 1,704,878 883,530 1,671,541 862,324

Table 3.1: Effects of Cache Size, Associativity, and Line Size

Given our 4MB/64B cache and 8-way set associativity

the cache we are left with has 8,192 sets and only 13

bits of the tag are used in addressing the cache set. To

determine which (if any) of the entries in the cache set

contains the addressed cache line 8 tags have to be com-

pared. That is feasible to do in very short time. With an

experiment we can see that this makes sense.

Table 3.1 shows the number of L2 cache misses for a

program (gcc in this case, the most important benchmark

of them all, according to the Linux kernel people) for

changing cache size, cache line size, and associativity set

size. In section 7.2 we will introduce the tool to simulate

the caches as required for this test.

Just in case this is not yet obvious, the relationship of all

these values is that the cache size is

cache line size × associativity × number of sets

The addresses are mapped into the cache by using

O = log

cache line size

S = log

number of sets

in the way the ﬁgure on page 15 shows.

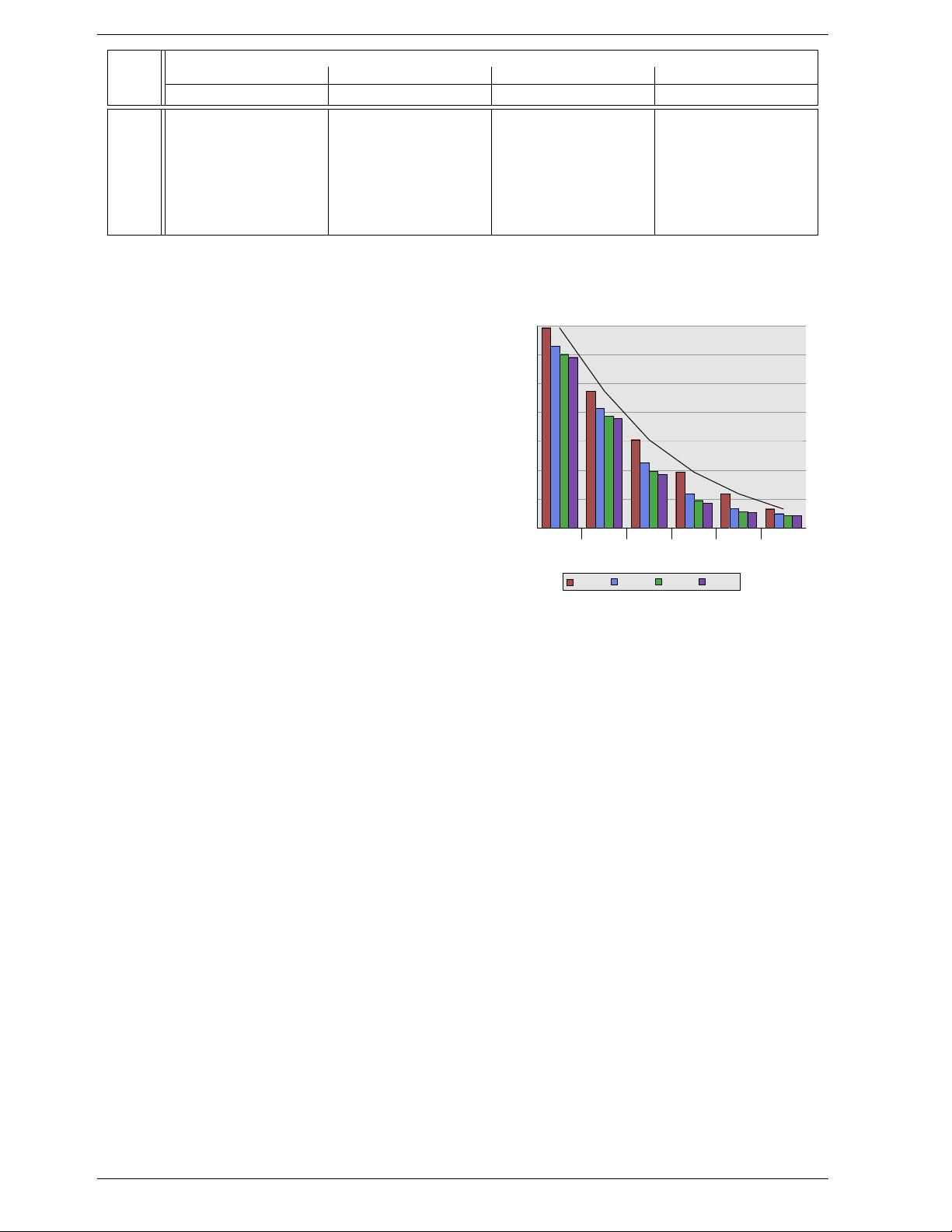
Figure 3.8 makes the data of the table more comprehen-

sible. It shows the data for a ﬁxed cache line size of

32 bytes. Looking at the numbers for a given cache size

we can see that associativity can indeed help to reduce

the number of cache misses signiﬁcantly. For an 8MB

cache going from direct mapping to 2-way set associative

cache saves almost 44% of the cache misses. The proces-

sor can keep more of the working set in the cache with

a set associative cache compared with a direct mapped

cache.

In the literature one can occasionally read that introduc-

ing associativity has the same effect as doubling cache

size. This is true in some extreme cases as can be seen

in the jump from the 4MB to the 8MB cache. But it

certainly is not true for further doubling of the associa-

tivity. As we can see in the data, the successive gains are

512k

1M 2M 4M

8M 16M

Cache Size

Cache Misses (in Millions)

Direct

2-way 4-way 8-way

Figure 3.8: Cache Size vs Associativity (CL=32)

much smaller. We should not completely discount the ef-

fects, though. In the example program the peak memory

use is 5.6M. So with a 8MB cache there are unlikely to

be many (more than two) uses for the same cache set.

With a larger working set the savings can be higher as

we can see from the larger beneﬁts of associativity for

the smaller cache sizes.

In general, increasing the associativity of a cache above

8 seems to have little effects for a single-threaded work-

load. With the introduction of hyper-threaded proces-

sors where the ﬁrst level cache is shared and multi-core

processors which use a shared L2 cache the situation

changes. Now you basically have two programs hitting

on the same cache which causes the associativity in prac-

tice to be halved (or quartered for quad-core processors).

So it can be expected that, with increasing numbers of

cores, the associativity of the shared caches should grow.

Once this is not possible anymore (16-way set associa-

tivity is already hard) processor designers have to start

using shared L3 caches and beyond, while L2 caches are

potentially shared by a subset of the cores.

Another effect we can study in Figure 3.8 is how the in-

crease in cache size helps with performance. This data

cannot be interpreted without knowing about the working

Ulrich Drepper Version 1.0 19

set size. Obviously, a cache as large as the main mem-

ory would lead to better results than a smaller cache, so

there is in general no limit to the largest cache size with

measurable beneﬁts.

As already mentioned above, the size of the working set

at its peak is 5.6M. This does not give us any absolute

number of the maximum beneﬁcial cache size but it al-

lows us to estimate the number. The problem is that

not all the memory used is contiguous and, therefore,

we have, even with a 16M cache and a 5.6M working

set, conﬂicts (see the beneﬁt of the 2-way set associa-

tive 16MB cache over the direct mapped version). But

it is a safe bet that with the same workload the beneﬁts

of a 32MB cache would be negligible. But who says the

working set has to stay the same? Workloads are grow-

ing over time and so should the cache size. When buying

machines, and one has to choose the cache size one is

willing to pay for, it is worthwhile to measure the work-

ing set size. Why this is important can be seen in the

ﬁgures on page 21.

Sequential

Random

Figure 3.9: Test Memory Layouts

Two types of tests are run. In the ﬁrst test the elements

are processed sequentially. The test program follows the

pointer n but the array elements are chained so that they

are traversed in the order in which they are found in mem-

ory. This can be seen in the lower part of Figure 3.9.

There is one back reference from the last element. In the

second test (upper part of the ﬁgure) the array elements

are traversed in a random order. In both cases the array

elements form a circular single-linked list.

3.3.2 Measurements of Cache Effects

All the ﬁgures are created by measuring a program which

can simulate working sets of arbitrary size, read and write

access, and sequential or random access. We have al-

ready seen some results in Figure 3.4. The program cre-

ates an array corresponding to the working set size of

elements of this type:

struct l {

struct l

long int pad[NPAD];

};

All entries are chained in a circular list using the n el-

ement, either in sequential or random order. Advancing

from one entry to the next always uses the pointer, even if

the elements are laid out sequentially. The pad element

is the payload and it can grow arbitrarily large. In some

tests the data is modiﬁed, in others the program only per-

forms read operations.

In the performance measurements we are talking about

working set sizes. The working set is made up of an ar-

ray of struct l elements. A working set of 2

bytes

contains

/sizeof(struct l)

elements. Obviously sizeof(struct l) depends on

the value of NPAD. For 32-bit systems, NPAD=7 means the

size of each array element is 32 bytes, for 64-bit systems

the size is 64 bytes.

Single Threaded Sequential Access The simplest

case is a simple walk over all the entries in the list. The

list elements are laid out sequentially, densely packed.

Whether the order of processing is forward or backward

does not matter, the processor can deal with both direc-

tions equally well. What we measure here–and in all the

following tests–is how long it takes to handle a single list

element. The time unit is a processor cycle. Figure 3.10

shows the result. Unless otherwise speciﬁed, all mea-

surements are made on a Pentium 4 machine in 64-bit

mode which means the structure l with NPAD=0 is eight

bytes in size.

The ﬁrst two measurements are polluted by noise. The

measured workload is simply too small to ﬁlter the ef-

fects of the rest of the system out. We can safely assume

that the values are all at the 4 cycles level. With this in

mind we can see three distinct levels:

• Up to a working set size of 2

bytes.

• From 2

bytes to 2

bytes.

• From 2

bytes and up.

These steps can be easily explained: the processor has a

16kB L1d and 1MB L2. We do not see sharp edges in the

transition from one level to the other because the caches

are used by other parts of the system as well and so the

cache is not exclusively available for the program data.

Speciﬁcally the L2 cache is a uniﬁed cache and also used

for the instructions (NB: Intel uses inclusive caches).

What is perhaps not quite expected are the actual times

for the different working set sizes. The times for the L1d

hits are expected: load times after an L1d hit are around

4 cycles on the P4. But what about the L2 accesses?

Once the L1d is not sufﬁcient to hold the data one might

expect it would take 14 cycles or more per element since

this is the access time for the L2. But the results show

that only about 9 cycles are required. This discrepancy

20 Version 1.0 What Every Programmer Should Know About Memory

剩余113页未读，继续阅读

m0_37868300

粉丝: 0
资源: 3

程序员必读：理解内存与CPU缓存优化的实战指南

每个程序员都应该了解的内存知识【chp1-chpt4】.pdf

What every programmer should know about memory

cpumemory-What Every Programmer Should Know About Memory.pdf

What Every Programmer Should Know About Memory

Expert Oracle Database Architecture 2nd 原版PDF by Kyte

Google C++ Style Guide(Google C++编程规范）高清PDF

微软内部资料-SQL性能优化3

乌尔里克·德雷珀(Ulrich Drepper) CPU memory 内存知识详解

SD大会精品讲座：程序员必须适应不断变化的机器架构(英语授课)

SSD7 选择题。Multiple-Choice

最新资源