滤波器相位特性探讨：过程控制中的关键影响

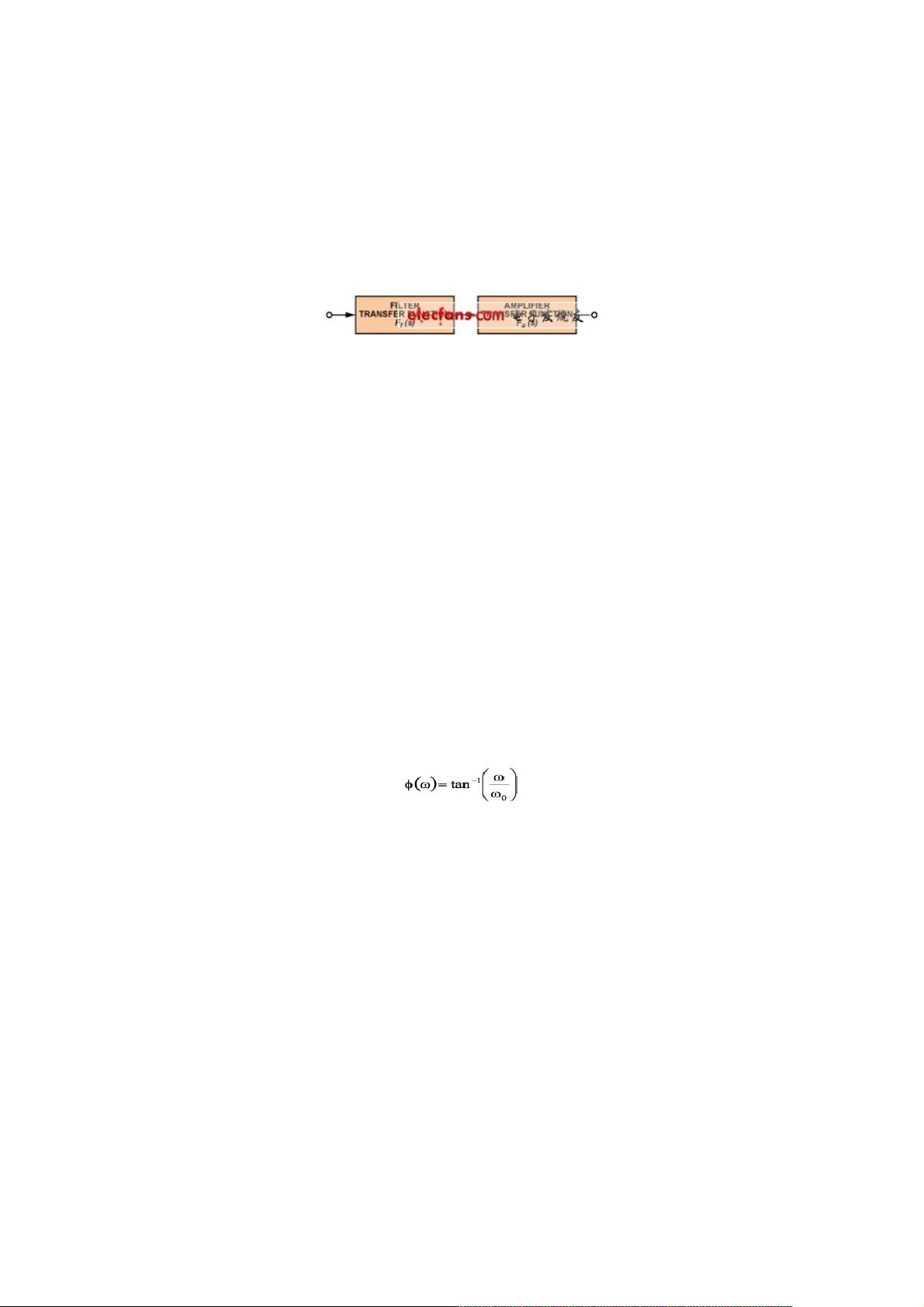
在有源滤波器的设计和应用中，相位响应的重要性不容忽视。尽管在一般情况下，幅值响应是决定滤波器性能的关键指标，但在诸如过程控制系统这样的场合，滤波器的相位特性直接影响系统的稳定性和动态响应。例如，在控制环路中，总的相移量决定了闭环系统的时间常数，从而影响系统的响应速度和抗干扰能力。 滤波器的相位响应与其拓扑结构紧密相关。滤波器可以设计成串联或并联形式，以及多级联接。不同类型的滤波器，如Butterworth、Bessel或Chebyshev等，不仅影响幅值响应的平坦度，还会影响相位响应的斜率。通过级联一阶或二阶基本单元，可以构建高阶滤波器，但随着阶数的增加，元件的选择和布局变得更加关键，因为这会直接影响到频率响应的精度和稳定性。 传递函数是描述滤波器频率响应的核心数学工具。对于同阶滤波器，其传递函数的相位响应部分遵循一定的规律。例如，单极低通滤波器的相位φ与频率ω和中心频率ω0之间的关系可以通过公式(1)来表达，其中φ随频率的升高而增加。中心频率（或称为截止频率）是滤波器在幅值响应上达到-3dB衰减点的频率，这个点也是相位响应的一个转折点。 理解相位响应时，需要考虑频率单位的转换，因为频率通常以弧度/秒表示，而实际应用中可能用赫兹(Hz)。此外，滤波器设计时必须注意，不同的相位响应特性可能会导致在特定频率点出现相位反转，这可能导致控制系统的不稳定。 在实际应用中，设计师必须权衡滤波器的阶数、响应特性以及相位特性，以满足特定系统的需求。对于复杂系统，可能需要通过仿真和实验来优化滤波器的相位响应，确保其在整个工作频率范围内都能提供所需的性能。有源滤波器的相位关系是设计过程中不可或缺的一部分，它对于保证系统的整体性能至关重要。