LSTM在有限新息率畸变信号重构中的应用

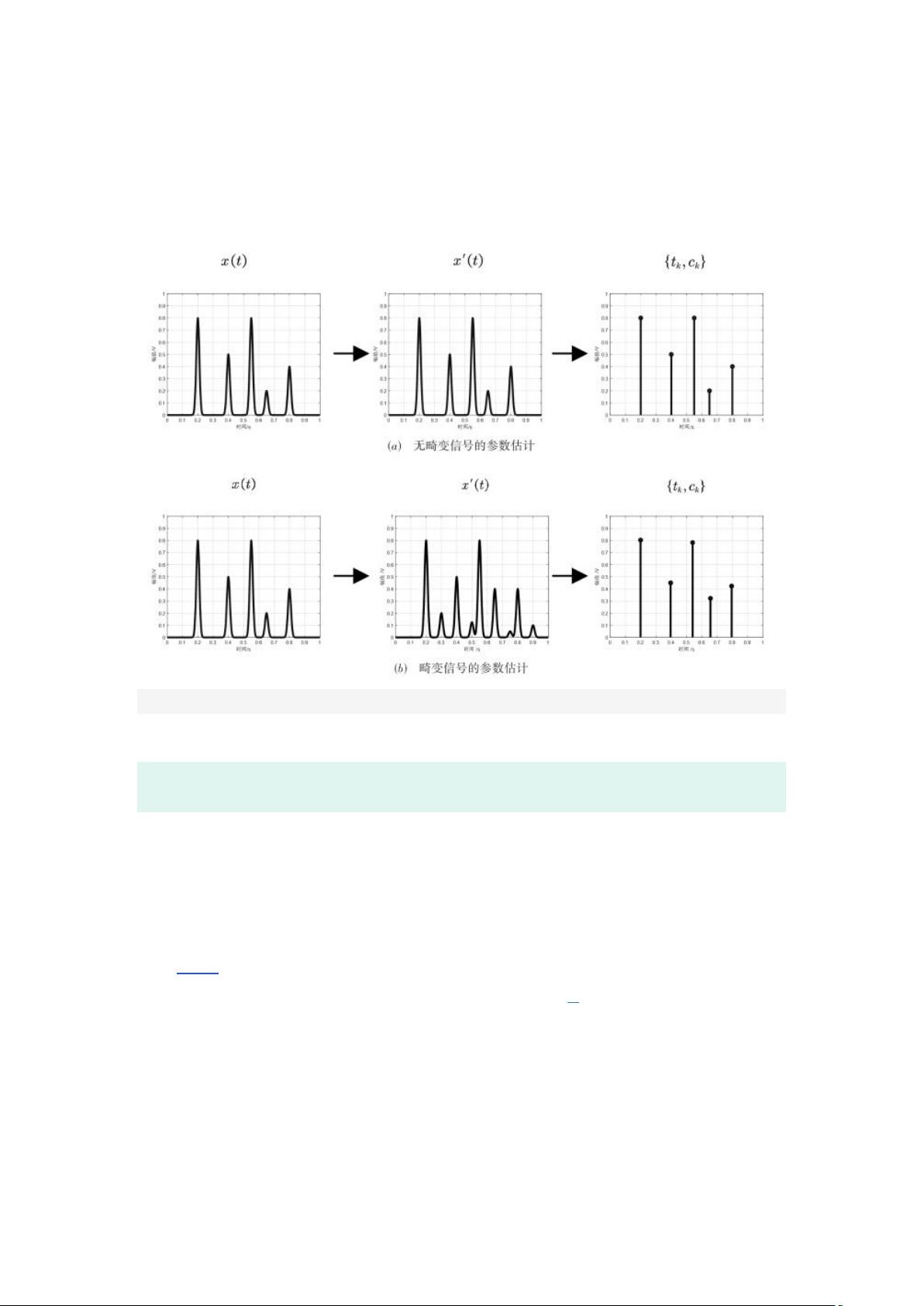
"这篇文档是关于基于LSTM特征提取的有限新息率（FRI）畸变信号重构的研究。FRI是一种现代采样方法，它根据信号的自由度而非带宽进行采样，允许在低于奈奎斯特率的采样速率下捕获信息。文档指出，传统的FRI方法依赖于已知的信号波形结构，但在存在噪声、非线性效应等现实世界因素时，重构性能会降低。为此，研究人员已经开发了各种优化重构技术，如Cadzow降噪、波形再生和模型匹配。然而，对于严重畸变的信号，特别是因脉冲重叠导致的波形结构变化，FRI重构仍面临挑战。文中提到，利用指数再生核和有限个洛伦兹函数的拟合方法是解决波形结构未知问题的常见策略，但这些方法可能有较高的复杂度或特定的前提条件。" 在现代信息技术中，FRI采样理论是一个关键的突破，它挑战了传统的香农采样定理。FRI方法通过考虑信号的自由度来减少采样速率，这在处理高速、宽带信号时具有显著优势，尤其在超宽带信号系统和雷达系统中。然而，现实环境中的噪声、非线性效应可能导致信号波形结构的变化，影响FRI的重构性能。为了解决这一问题，研究者已经提出了多种优化策略，包括使用降噪技术、波形再生算法以及模型匹配方法来提高系统的稳健性。 针对波形结构不可知的FRI重构问题，文献中提及了两种方法：一是使用指数再生核来拟合FRI信号，通过部分傅里叶系数恢复小波系数，但这需要输入脉冲满足小波稀疏条件；二是基于有限个洛伦兹函数的拟合，适用于脉宽可变的FRI信号。这两种方法虽然能够处理一定程度的信号畸变，但在面临严重畸变，如脉冲重叠时，可能效果有限。 LSTM（长短时记忆网络）在本文档中可能被用作特征提取工具，因为其在处理序列数据和捕捉长期依赖关系方面表现出色。通过LSTM，可以从畸变信号中提取关键特征，进而改进重构过程的准确性和鲁棒性。这种深度学习方法为解决FRI重构中的复杂问题提供了一条新的路径，尤其是在面对非线性影响和噪声时，可能比传统方法更为有效。 这篇文档探讨了在信号畸变情况下基于FRI的信号重构问题，强调了LSTM在特征提取中的潜在作用，并提供了现有解决方法的概述。通过对LSTM等先进工具的应用，研究者们正在不断探索提高FRI重构性能的新途径，以适应更加复杂和现实的通信系统环境。