BP神经网络:误差反向传播算法详解
需积分: 9 70 浏览量
更新于2024-09-03
收藏 1007KB PPTX 举报
"BP神经网络是一种基于误差反向传播算法的多层感知器,用于训练人工神经网络以解决复杂的学习任务。它通过迭代的方式逐步优化网络权重和偏置,以减小网络输出与期望输出之间的误差。"
BP神经网络的核心在于其误差反向传播过程,该过程分为三个主要步骤:
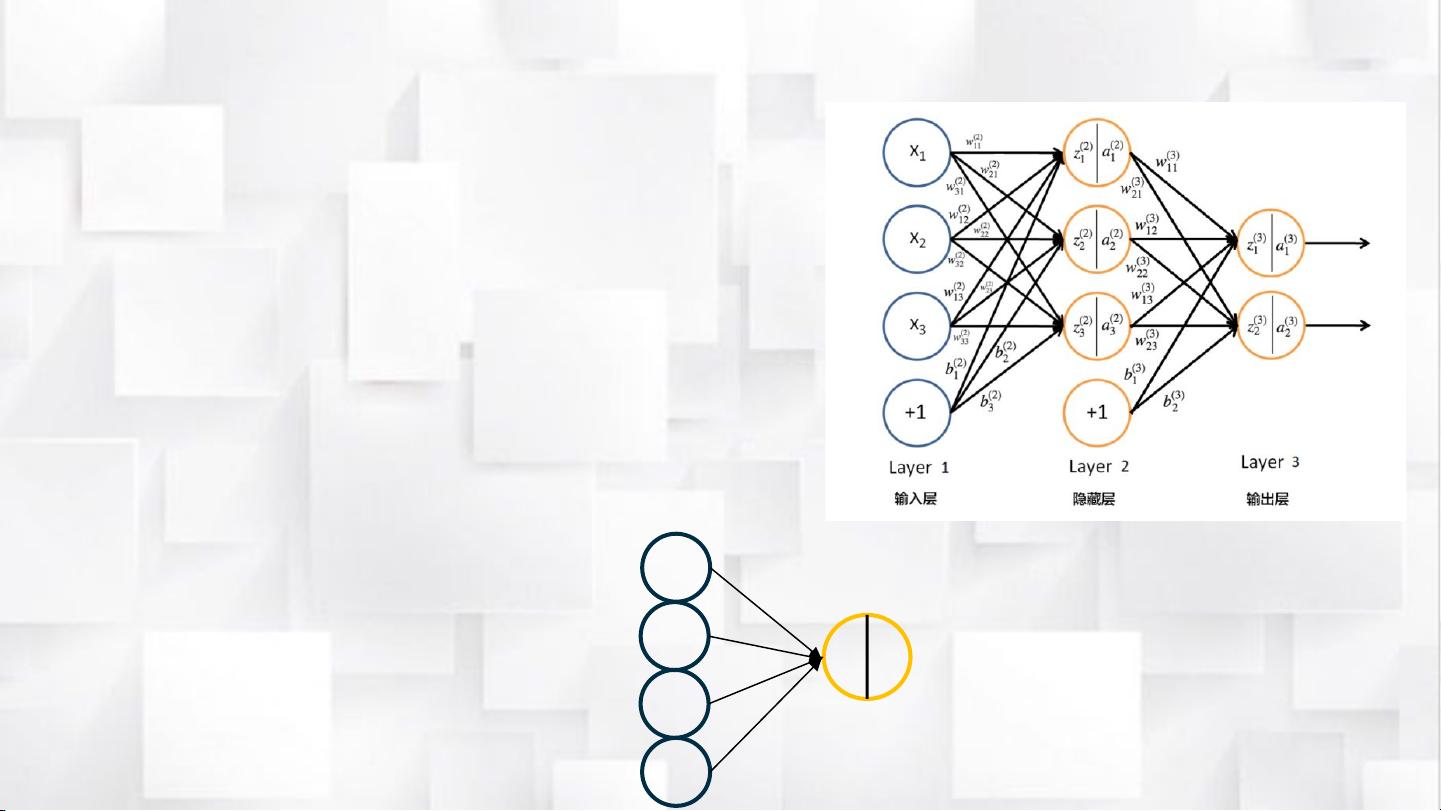
1. **前向传播**:输入信号通过网络逐层传递,计算各层神经元的状态和激活值。这个过程从输入层开始,沿着连接权重将信息传递到输出层。
2. **误差计算**:在得到网络的预测输出后,通过比较预测值与实际期望值计算出误差。这个误差从输出层开始,按照反向顺序传播回输入层,以便于分析每一层神经元对总误差的贡献。
3. **参数更新**:利用链式法则计算每个权重和偏置对总误差的偏导数,这些偏导数指示了参数应如何调整以减小误差。这通常涉及到梯度下降法,通过沿着误差下降最快的方向调整权重和偏置。
具体来说,BP算法涉及以下关键公式:
- **偏置参数更新公式**:更新偏置参数以减少误差,这通常涉及到误差项与学习率的乘积。
- **权重参数更新公式**:类似地,权重参数的更新也依赖于误差项和学习率,以及输入的激活值。
- **隐藏层和输出层的δ表达式**:δ表示误差项,反映了每个神经元对其所在层误差的贡献,它们分别对应于输出层和隐藏层的计算规则。
- **代价函数对参数的偏导数**:BP算法的核心是求解代价函数关于每个参数的偏导数,这构成了参数更新的基础。
在实践中,BP算法的实现包括以下几个步骤:
1. **计算所有训练样本的偏导数**:对每个训练样本,使用前向传播计算状态和激活值,然后反向传播计算偏导数。
2. **参数更新**:根据批量梯度下降法,用所有训练样本的平均偏导数更新参数。
3. **迭代直至满足停止条件**:重复以上步骤,直到误差变化很小或者达到最大迭代次数。
需要注意的是,当训练数据集庞大时,BP算法的效率会降低,因为它需要对每个样本进行前向传播和反向传播。在这种情况下,可以使用随机梯度下降法,每次只用一个训练样本更新参数,以提高训练速度。
BP神经网络和其反向传播算法是深度学习中的基础工具,通过迭代优化网络权重和偏置,使得模型能够从大量数据中学习并进行有效的预测。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2023-05-25 上传
2024-04-19 上传
2021-04-26 上传
2021-03-13 上传
2021-10-11 上传
惊起莫回头
- 粉丝: 1
- 资源: 8
最新资源
- NVidia GPU Programming Guide
- Excel使用大全,整理了excel的一些常用函数和例子
- CDMA2000核心网原理和关键技术
- 中兴公司-MAP业务流程
- VC#的四个基本技巧
- 无线传感器网络路由协议
- Mobile移动开发宝典_第06章 完成应用程序:打包与部署
- Mobile移动开发宝典_第05章 理解.NET Compact Framework与性能优化
- Mobile移动开发宝典_第04章 捕获错误,测试与调试
- Mobile移动开发宝典_第03章 使用SQL Server 2005 Compact Edition和其他数据存储
- 电力电子技术PWM电压输出
- 单片机系列atmega16
- vb学习浅谈(经验)
- 毕业设计选题系统论文
- Mobile移动开发宝典_第02章 构建Windows窗体GUI
- 腾讯笔试题(内容丰富详实!值得仔细看看)