高效高精乘除算法与Catalan数在问题解决中的应用

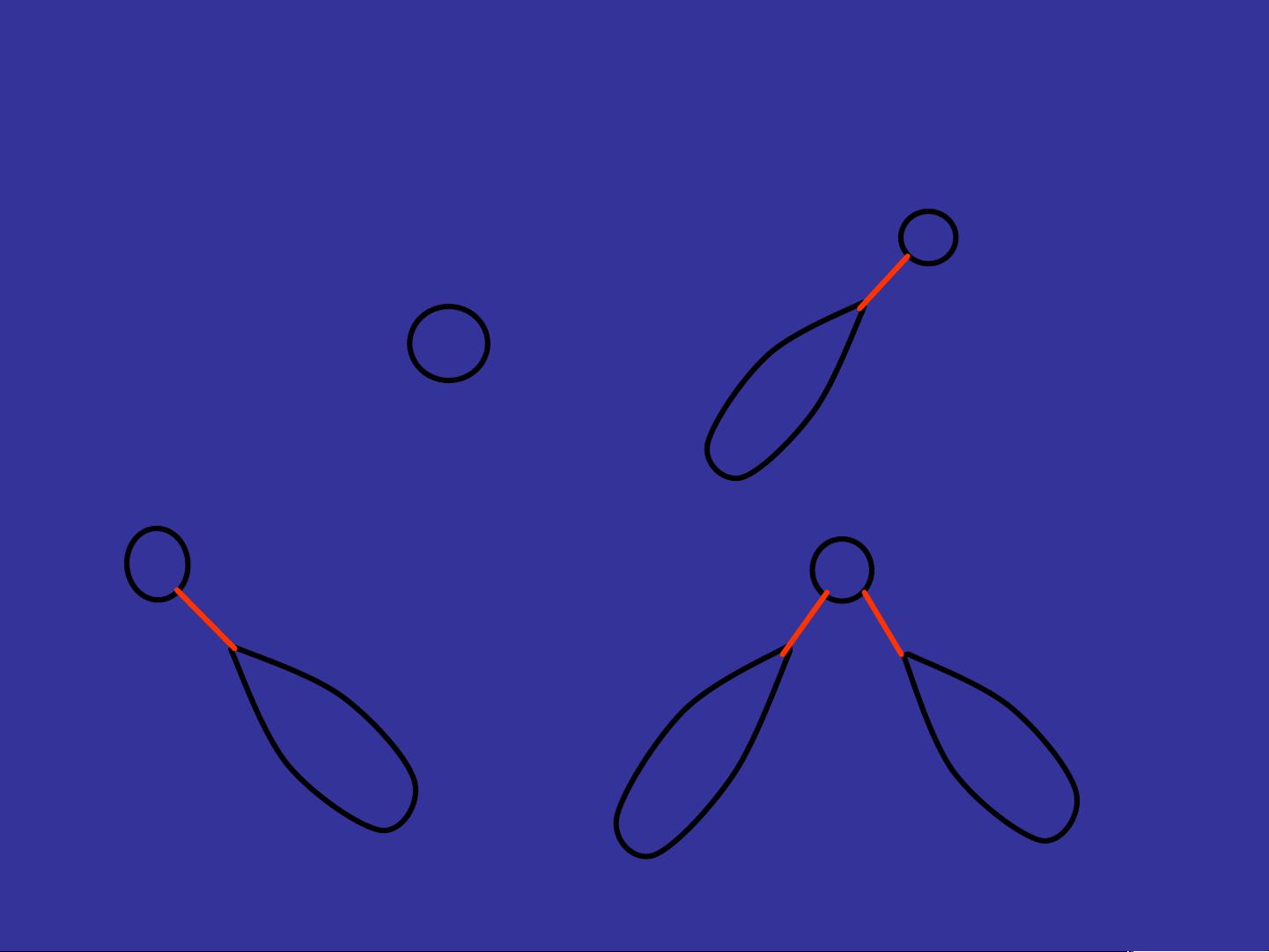
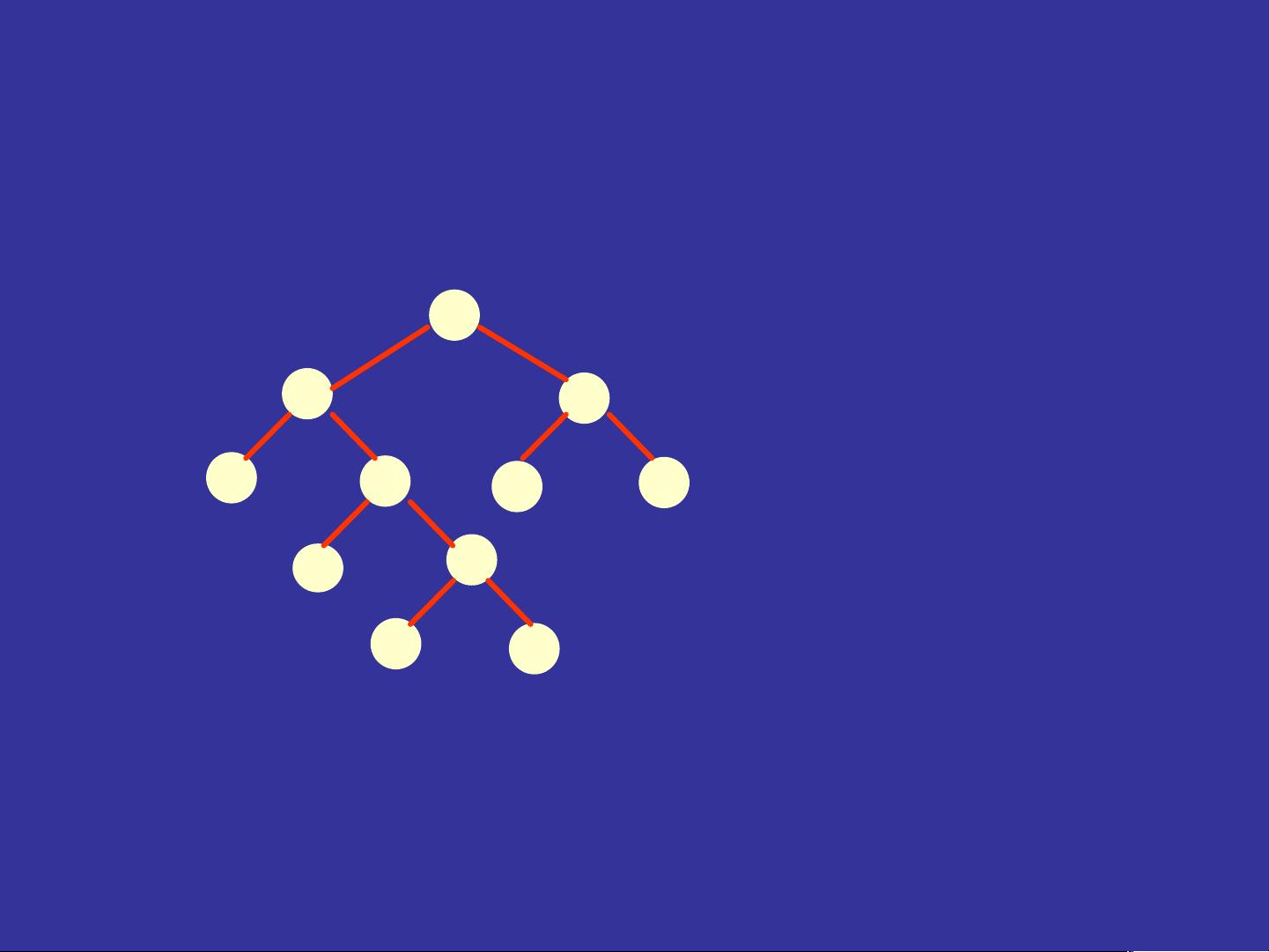
在算法专项练习中，重点讲解了高精度乘法与高精度除法的高效计算策略。首先，"边乘边除"方法可以显著提升运算效率，即在执行乘法和除法的同时进行，减少重复计算。对于更大的数值n，分解乘数和除数为质因数并统计各质因数的数量，然后相乘，这是标准的算法优化手段，尤其适用于处理大数运算。 其次，引入了Catalan数的概念，这是一种特殊的数列，其递归定义为h(n) = h(0) * h(n-1) + h(1) * h(n-2) + ... + h(n-1) * h(0)，其中n >= 2。Catalan数在许多数学和计算机科学问题中都有应用，例如解决一些排列组合问题，比如在n个A和n个B的排列中，B的个数不超过A的个数的情况。 将问题转化为Catalan数问题模型的关键在于识别递归结构和寻找与Catalan数描述相符的模式。例如，将二叉树的不同形态计数问题转化为求解操作序列中的Catalan数，即找出满足特定条件的1和0的二进制序列个数。在这些问题中，通过构造递推关系，或者观察操作序列的性质，如任意时刻"0"的累计数不超过"1"的累计数，来确定Catalan数的应用。 总结来说，学习高精度乘除不仅涉及到基础的算法设计，还与数论、组合数学中的高级概念相结合。理解并掌握如何将实际问题映射到Catalan数问题模型，是解决这类复杂问题的关键。在实践中，熟练运用这些技巧能大大提高编程效率和问题解决能力。