支持向量机(SVM)深度解析：理论与应用

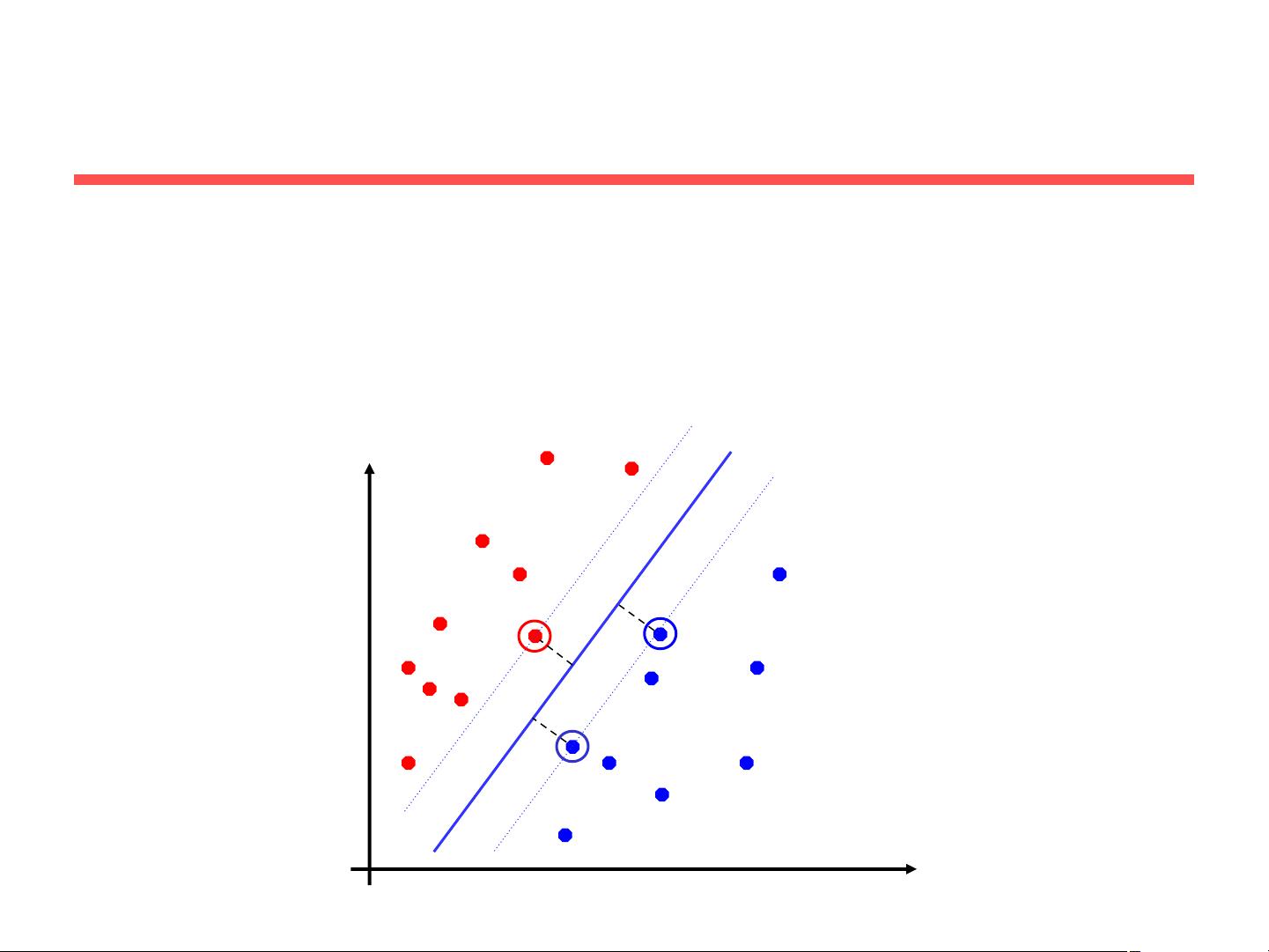
"该资源是一套完整的机器学习入门教程，包含多个主题的PPT和PDF文件，涵盖了从机器学习基础知识到具体算法的详细介绍。其中包括了支持向量机（SVM）的相关内容，适合初学者系统学习。" 在机器学习领域，支持向量机（Support Vector Machine，简称SVM）是一种强大的监督学习算法，广泛应用于分类和回归问题。SVM的历史可以追溯到1960年代Vapnik和Chervonenkis的统计学习理论。它的主要特点是训练过程可能较慢，但能够提供较高的预测准确性，尤其是对于构建非线性决策边界的能力。 SVM的基本思想是通过最大化间隔（Margin）来找到最佳的分类超平面。间隔是指数据点到超平面的最近距离，而那些离超平面最近的数据点被称为支持向量。在二分类问题中，分类任务可以看作是在特征空间中将两类数据分开，超平面的方程为wTx+b=0。如果数据点wTx+b<0或wTx+b>0，则分别属于负类和正类。理想的超平面应能最大程度地分离两类样本，即最大化间隔ρ。 支持向量是决定超平面的关键，因为它们决定了间隔的大小。优化间隔意味着只有支持向量对模型有直接影响，而其他训练样本则相对不重要，这是基于统计学习理论中的PAC（Probably Approximately Correct）理论。在数学表述上，SVM的目标是找到使得所有支持向量满足特定等式的超平面，并通过重新缩放权重w和偏置b，确保间隔ρ/2的距离被保持。 线性SVM是最简单的形式，它在数据可线性分离的情况下工作。当数据非线性时，SVM通过核函数（如高斯核、多项式核等）将数据映射到高维空间，使得在高维空间中可以找到一个线性超平面进行有效分类。 在实际应用中，SVM已被成功用于手写数字识别、物体识别、语音识别以及时间序列预测等多个领域。通过理解和掌握SVM的工作原理，我们可以解决许多实际问题，同时也能为更深入的机器学习研究打下坚实的基础。本资源提供的支持向量机PPT详细介绍了SVM的理论、方法及其应用，是学习和理解SVM的理想资料。