Fast Search in Hamming Space with Multi-Index Hashing
Mohammad Norouzi Ali Punjani David J. Fleet
Department of Computer Science
University of Toronto
{norouzi,alipunjani,fleet}@cs.toronto.edu
Abstract
There has been growing interest in mapping image data
onto compact binary codes for fast near neighbor search in
vision applications. Although binary codes are motivated
by their use as direct indices (addresses) into a hash ta-
ble, codes longer than 32 bits are not being used in this
way, as it was thought to be ineffective. We introduce a
rigorous way to build multiple hash tables on binary code
substrings that enables exact K-nearest neighbor search in
Hamming space. The algorithm is straightforward to im-
plement, storage efficient, and it has sub-linear run-time
behavior for uniformly distributed codes. Empirical results
show dramatic speed-ups over a linear scan baseline and
for datasets with up to one billion items, 64- or 128-bit
codes, and search radii up to 25 bits.
1. Introduction
There has been growing interest in mapping image data
onto compact binary codes for fast near neighbor search in
vision applications (e.g., [20, 21, 23]). Binary codes are
storage efficient and comparisons require just a small num-
ber of machine instructions; millions of binary codes can be
compared to a query in less than a second. But the most
compelling reason for binary codes is their use as direct
indices (addresses) into a hash table, yielding a dramatic
increase in search speed compared to an exhaustive linear
scan (e.g., [24, 19, 16]).
The problem is that, in practice, using binary codes as
hash indices is not necessarily efficient. To find near neigh-
bors one needs to examine all hash table entries (or buck-
ets) within some Hamming ball around the query. And the
number of such buckets grows near-exponentially with the
search radius (Fig. 2a). Even with a small search radius, the
number of buckets to examine may be larger than the num-
ber of items in the database, hence slower than linear scan.
Recent papers on binary codes mention the use of hash ta-
bles, but resort to linear scan when codes are longer than 32
bits (e.g., [23, 19, 12, 16]), although longer codes are often
necessary to preserve sufficient similarity (e.g., see Fig. 5).
time per query (s)
dataset size (millions)
Linear scan
1000−NN
100−NN
10−NN
200 500 1000
0
0.05
0.1
0.15
0.2
dataset size (millions)
Linear scan
1000−NN
100−NN
10−NN
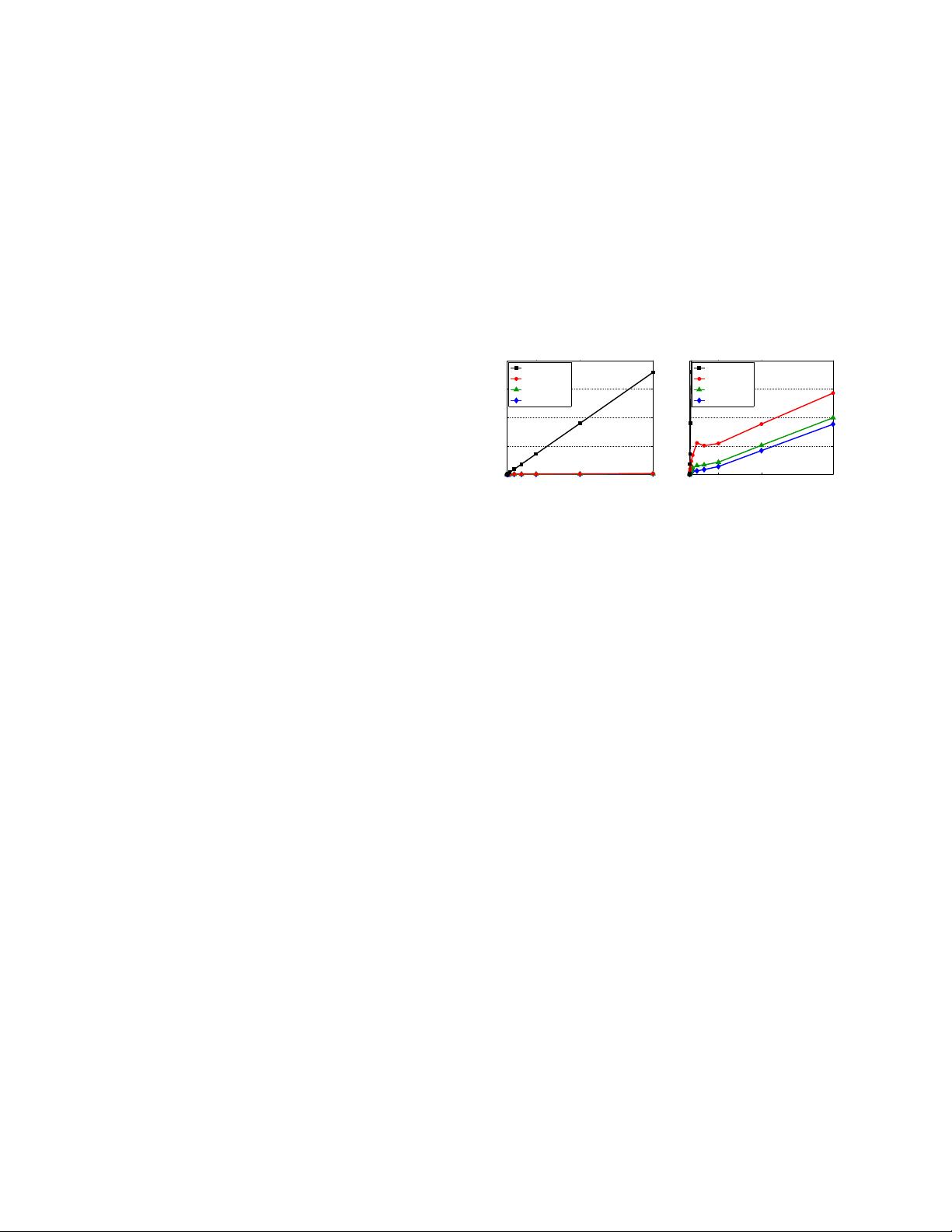
Figure 1. Nearest-neighbor search on a database of 64-bit binary
codes learned from SIFT descriptors. Run-times per query are
shown for the proposed multi-index hashing algorithm, searching
for 10, 100, and 1000 nearest neighbors. They are compared to
a linear scan baseline. Left and right plots show different vertical
scales; i.e., the vertical axis of the right plot is 100 times smaller
than the left, showing query times between 0 and 0.2s.
This paper presents a new algorithm for exact K-nearest
neighbor search on binary codes that is dramatically faster
than linear scan. This has been an open problem since
the introduction of hashing techniques with binary codes.
Our new multi-index hashing algorithm exhibits sub-linear
search times, is storage efficient, and straightforward to im-
plement. As an example, Fig. 1 plots CPU run-times per
query as a function of the size of a database comprising
64-bit codes learned from SIFT descriptors with Minimal
Loss Hashing [16]. Our current implementation searches a
dataset of a billion codes hundreds of times faster than lin-
ear scan, on a single computer.
1.1. Background: Problem and Related Work
Nearest neighbor (NN) search on binary codes has been
used for image search [18, 23, 24], matching local fea-
tures [9, 21], and parameter estimation [20]. Such tech-
niques begin with a similarity-preserving mapping from
high-dimensional data to binary codes. For many prob-
lems one wants to preserve Euclidean distance (e.g., [5,
12, 18, 21, 24]), while others focus on semantic similarity
(e.g., [16, 20, 19, 23]). Our algorithm does not depend on
the specific method for generating the binary codes. Rather,
we are primarily concerned with fast search in Hamming
1









