MATLAB实现傅里叶变换详解

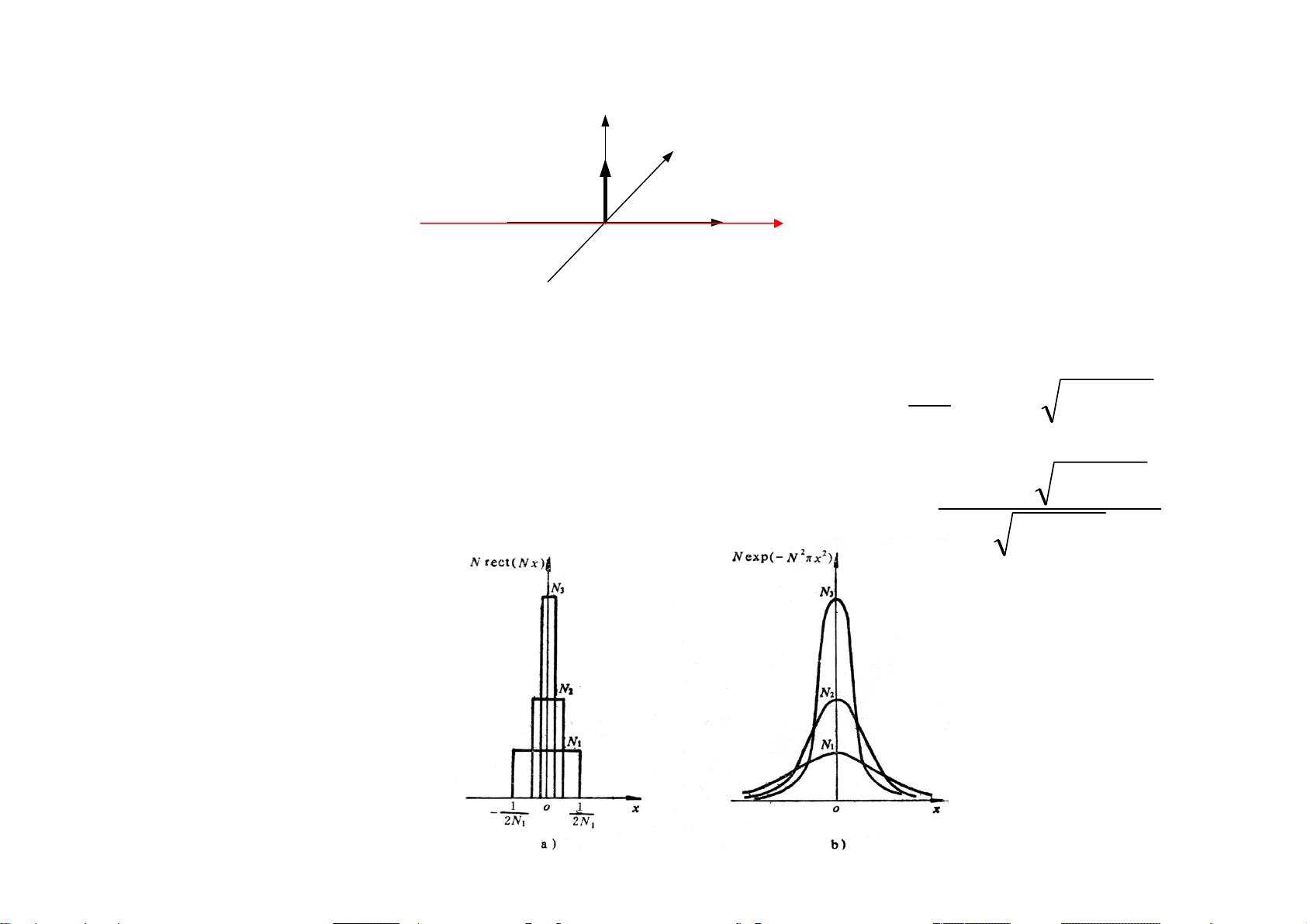
"MATLAB傅里叶分析介绍，深入讲解了傅立叶变换的matlab实现，共计93页，涵盖多种函数的傅里叶变换、脉冲函数、卷积、傅里叶变换的性质以及MATLAB中的实际应用。" 本文档详细介绍了MATLAB在傅里叶分析中的应用，首先提到了几种常用的函数，这些函数是傅里叶分析的基础。其中包括： 1. **阶跃函数**：在MATLAB中，阶跃函数`step(x)`定义了一个分段线性函数，当`x<0`时返回0，`x=0`时返回0.5，`x>0`时返回1。这个函数在信号处理中常用来表示开关或阈值行为。 2. **符号函数**：MATLAB的`sgn(x)`函数返回输入值的符号，如果`x>0`则返回1，`x=0`则返回0，`x<0`则返回-1。对于非零复数，它等于输入值除以其绝对值。 3. **矩形函数**（也称为单位阶跃函数）：通常表示为`rect(x/a)`，它在`-a`到`a`区间内为1，其余区间为0。在MATLAB中没有内置的矩形函数，但可以通过其他函数组合来实现。 文档还讨论了脉冲函数及其性质，以及**疏函数**的概念，这在信号处理和频谱分析中很重要。**卷积**作为傅里叶分析的核心概念，其定义、物理意义和性质也得到了详细阐述，包括MATLAB中的卷积实现方法。 接着，文档深入探讨了**傅里叶变换**，包括其定义、存在条件、广义傅里叶变换，以及针对虚函数、实函数、奇函数和偶函数的特性。特别地，介绍了**可分离函数**的傅里叶变换，以及**FT-BESSAL变换**，这是一种与傅里叶变换相关的特定变换类型。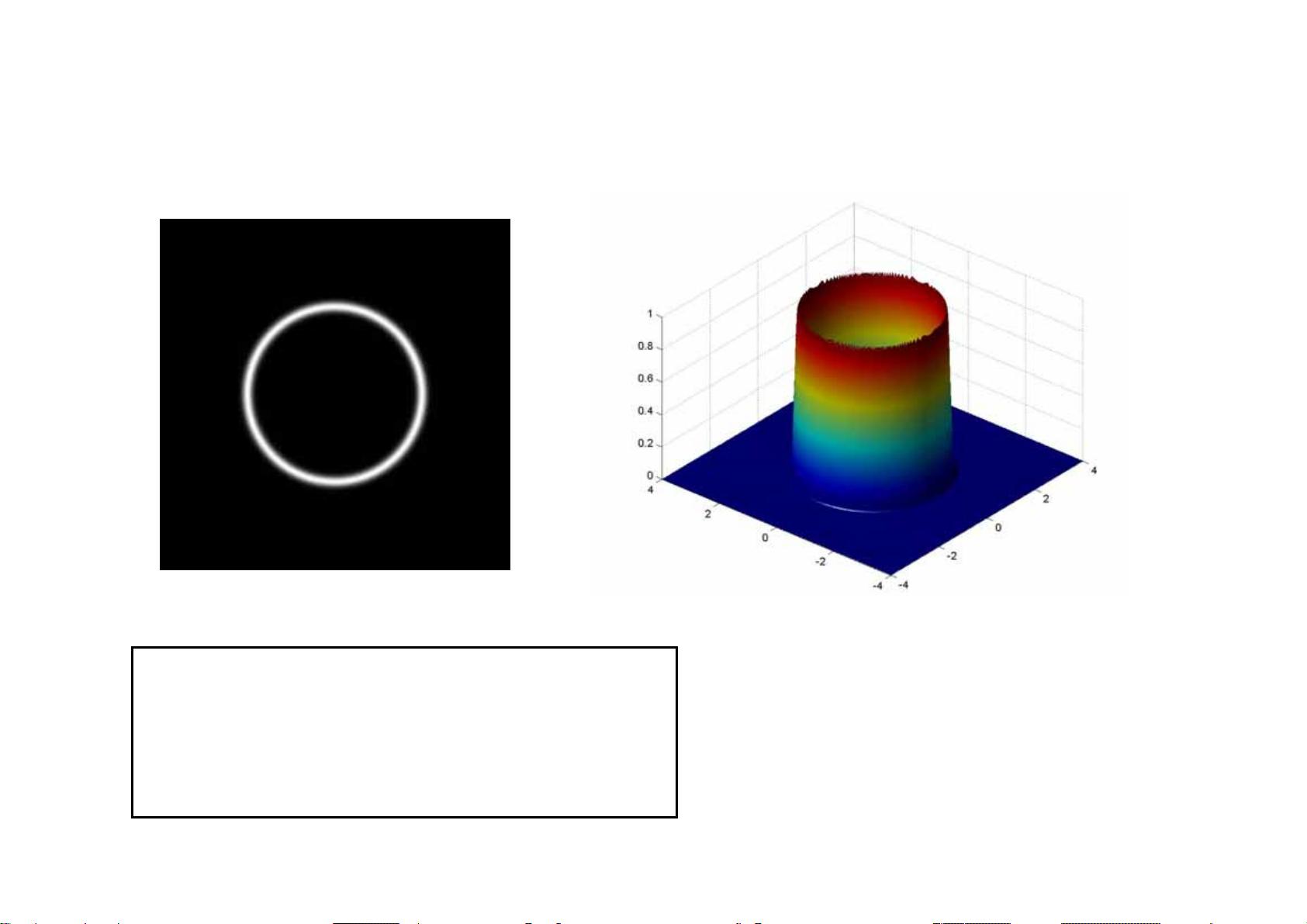 在具体函数的傅里叶变换部分，文档列举了**几种常用函数**（如Sinc函数、高斯函数、圆域函数等）的傅里叶变换形式，并展示了它们在频域的特性。同时，还探讨了几种常见图形的傅里叶变换，这对于理解和分析复杂信号的频谱特征至关重要。 最后，文档提到了**傅里叶变换的数值实现**，这是MATLAB在实际应用中的关键部分，通过MATLAB的函数和工具可以方便地计算并可视化傅里叶变换结果。 这份93页的PDF文档为读者提供了一个全面的MATLAB傅里叶分析教程，不仅理论基础扎实，而且结合了实际操作，对于学习和理解傅里叶变换在MATLAB中的应用极具价值。