有序数组转高度平衡二叉搜索树的算法解析

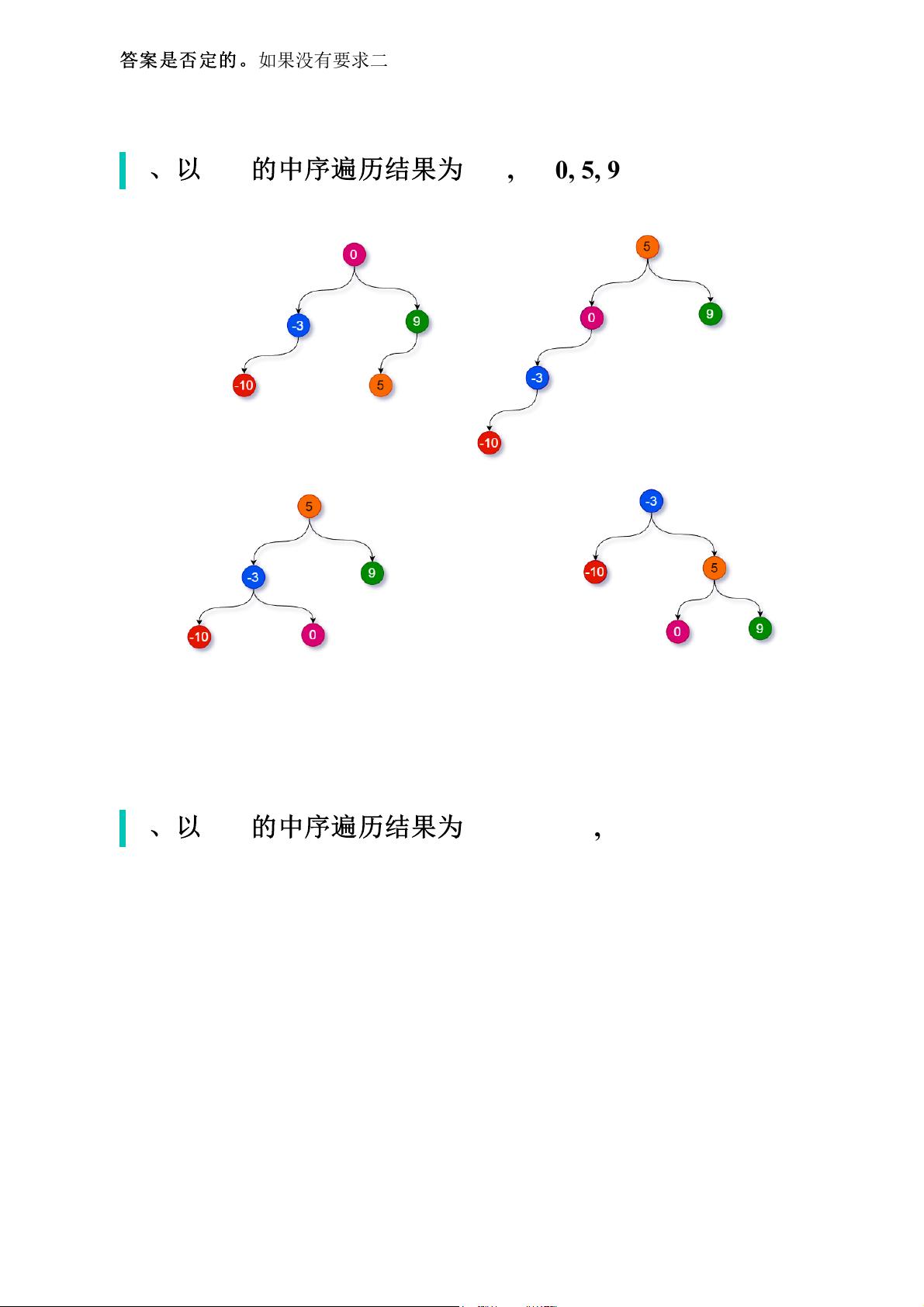
"有序数组转二叉搜索树" 在计算机科学中，有序数组转换成高度平衡的二叉搜索树（BST）是一个常见的算法问题。二叉搜索树是一种特殊的二叉树，其每个节点的值都大于其左子树中任何节点的值，且小于其右子树中任何节点的值。高度平衡的二叉搜索树是指左右两个子树的高度差的绝对值不超过1的二叉搜索树。 题目要求将一个已排序的整数数组nums转换为高度平衡的二叉搜索树。为了实现这个目标，我们需要考虑以下关键点： 1. **二叉搜索树的特性**：二叉搜索树的中序遍历结果是一个升序序列。由于输入数组是有序的，我们可以保证它符合二叉搜索树的中序遍历序列。 2. **高度平衡的要求**：如果仅要求二叉搜索树是二叉搜索树，那么任何元素都可以作为根节点，因为二叉搜索树的定义并不涉及树的高度。但是，如果要求高度平衡，情况就变得复杂了。 3. **根节点的选择**：对于长度为奇数的数组，根节点是数组的中间元素。对于长度为偶数的数组，可以选择中间位置的左侧或右侧元素作为根节点。这会影响到树的平衡性，因为选择不同，左右子树的大小可能会有所不同。 4. **递归构建**：确定根节点后，可以使用递归策略来构建左右子树。对于子序列[left, right]，中间元素作为根节点，左子树由[left, mid - 1]构造，右子树由[mid + 1, right]构造，其中mid是中间索引。 5. **数组下标管理**：在递归过程中，我们可以通过数组下标来确定子树的范围。初始时，left等于0，right等于nums.length - 1。递归结束条件是left大于right，表示没有更多的元素需要处理。 6. **方法一：选择中间元素**：这种方法总是选取当前子序列的中间元素作为根节点，然后递归处理左右子序列。这种方法可以确保在每一步都保持树的平衡。 通过这些步骤，我们可以编写一个算法来从有序数组构建高度平衡的二叉搜索树。具体实现时，可以使用递归函数，如Java或Python中的`buildBST(nums, left, right)`，其中`nums`是数组，`left`和`right`是数组的左右边界索引。在函数内部，首先检查边界条件，然后计算中间索引，创建新的树节点并递归构建左右子树。 将有序数组转换为高度平衡的二叉搜索树涉及到理解二叉搜索树的性质、平衡条件、根节点的选择以及递归构建树的过程。这个问题提供了对数据结构和算法设计深入理解的机会，同时也展示了如何通过递归解决复杂问题的能力。