鲁棒估计：随机分布时滞与马尔可夫跳跃耦合神经网络

54 浏览量更新于2024-08-26 收藏 1.1MB PDF 举报

"这篇研究论文探讨了具有参数不确定性、随机分布时滞和马尔可夫跳跃耦合的神经网络的鲁棒状态估计问题。在该论文中，采用多边形模型来描述参数不确定性，通过一组具有不同随机特性的伯努利过程来模拟分布时滞的随机出现。为了充分利用耦合信息，提出了基于局部耦合结构的新状态估计器。通过Kronecker乘积获得增广的估计误差系统，并引入了一个新的依赖于多边形不确定性及耦合信息的Lyapunov函数，以降低保守性。论文的主要贡献在于建立了一种更有效的鲁棒估计方法，适用于存在随机分布时滞和马尔可夫跳跃的复杂神经网络系统。" 在神经网络的研究中，鲁棒估计是一个关键问题，特别是当网络结构包含不确定性、随机时滞以及马尔可夫跳跃等复杂因素时。本论文的焦点在于解决这些挑战，以实现对神经网络状态的精确估计。首先，论文提出采用多边形模型来处理参数不确定性。这种模型可以包容多种可能的参数值，提供了一种灵活的方法来描述实际系统中可能出现的变化和不精确性。其次，随机分布时滞是神经网络动态行为中的一个常见特征，它可能导致系统的不稳定。通过伯努利过程，论文将时滞的随机性纳入模型，使得分析更具现实性。这一方法能够更好地捕捉实际系统中时滞随机出现的现象。接着，论文设计了基于局部耦合结构的状态估计器。这种结构允许估计器利用网络内部的耦合信息，从而提高估计的准确性和效率。这在处理大型复杂网络时尤为重要，因为耦合效应往往影响网络的整体动态性能。在分析过程中，论文使用Kronecker乘积来扩展估计误差系统。这是一种矩阵运算，可以有效地处理多个独立系统之间的耦合，简化了分析的复杂性。最后，通过引入一个新的依赖于多边形不确定性及耦合信息的Lyapunov函数，论文降低了保守性，即在确保系统稳定性的同时，放宽了对估计器性能的严格要求。这种方法有助于在保持系统稳定的同时，提高估计的鲁棒性。这篇论文为处理具有随机分布时滞和马尔可夫跳跃耦合的神经网络提供了理论基础和实用工具，对于理解和优化这类复杂系统的性能具有重要意义。同时，提出的估计策略可以为其他具有类似复杂性的系统提供参考，如自适应控制、滤波和预测等领域。

This article has been accepted for inclusion in a future issue of this journal. Content is final as presented, with the exception of pagination.

XU et al.: ROBUST ESTIMATION FOR NEURAL NETWORKS 3

is impacted by the ith component of x

(k) if the condition

= 0 holds.

Each nonlinear function g

(·), j ∈ ψ

in (1) is continuous,

bounded, g

(0) = 0, and there exist constants

and φ

satisﬁes the following inequality [40]:

≤

(a) − g

(b)

a − b

≤

(4)

where a, b ∈ R,anda = b.

Each node randomly occurs the distributed delays indepen-

dently, which is denoted by β

(k), i ∈ ψ

with the following

stochastic properties:

E{β

(k) = 1}=β

E{(β

(k) − β

)

}=β

(1 − β

)  β

∗

. (5)

The following convergent conditions of the constants μ

≥ 0

(d = 1, 2,...) hold:

+∞



d=1

< +∞,

+∞



d=1

dμ

< +∞. (6)

Remark 1: Parameter uncertainty has been studied by many

researchers in the past several decades, since the accurate

model is always hard to be obtained in general situations,

and systems are frequently disturbed by the environment

noises [34]. It is worth noting that the polytopic uncertainty

describes the parametric uncertainty more precisely than the

norm-bounded one [36], thus studying coupled neural net-

works with polytopic uncertainty is important.

The parameter uncertain model has been used to describe

the networked induced issues. For instances, the norm-

bounded uncertainty has been used to handle the sensor

failure [41]; the polytopic uncertain model has been introduced

to deal with the quantization error [42]; and the multiplicative

noise model has been considered to model the channel fad-

ing [43]. Therefore, the condition of parameter uncertainty can

be extended to the coupled neural networks with communica-

tion constraints.

Remark 2: The kind of distributed delays has become an

interesting topic in the past decade, since it is unavoidable

in many situations [40]. Recently, the randomly occurring

distributed delays have been considered for the T-S fuzzy

systems [44]. In order to further address the randomly occur-

ring distributed delays in coupled neural networks, a set of

distributed delays with different occurring probabilities are

presented.

B. Local Coupling Structure-Dependent State Estimators

The following local coupling structure-dependent estimators

are proposed to estimate the states of coupled neural networks:



ˆx

(k + 1) = A

,ϑ

(α(k))

ˆx

(k) + B

,ϑ

(α(k))

(k)

ˆz

(k) = C

,ϑ

(α(k))

ˆx

(k) + D

,ϑ

(α(k))

(k), i ∈ ψ

(7)

where ˆx

(k) represents the state of the estimators. The

matrices A

,ϑ

(α(k))

, B

,ϑ

(α(k))

, C

,ϑ

(α(k))

,andD

,ϑ

(α(k))

are parameters of estimators, which need to be designed.

1 ≤ ϑ

(α(k)) ≤ s denotes the local variation of the coupling

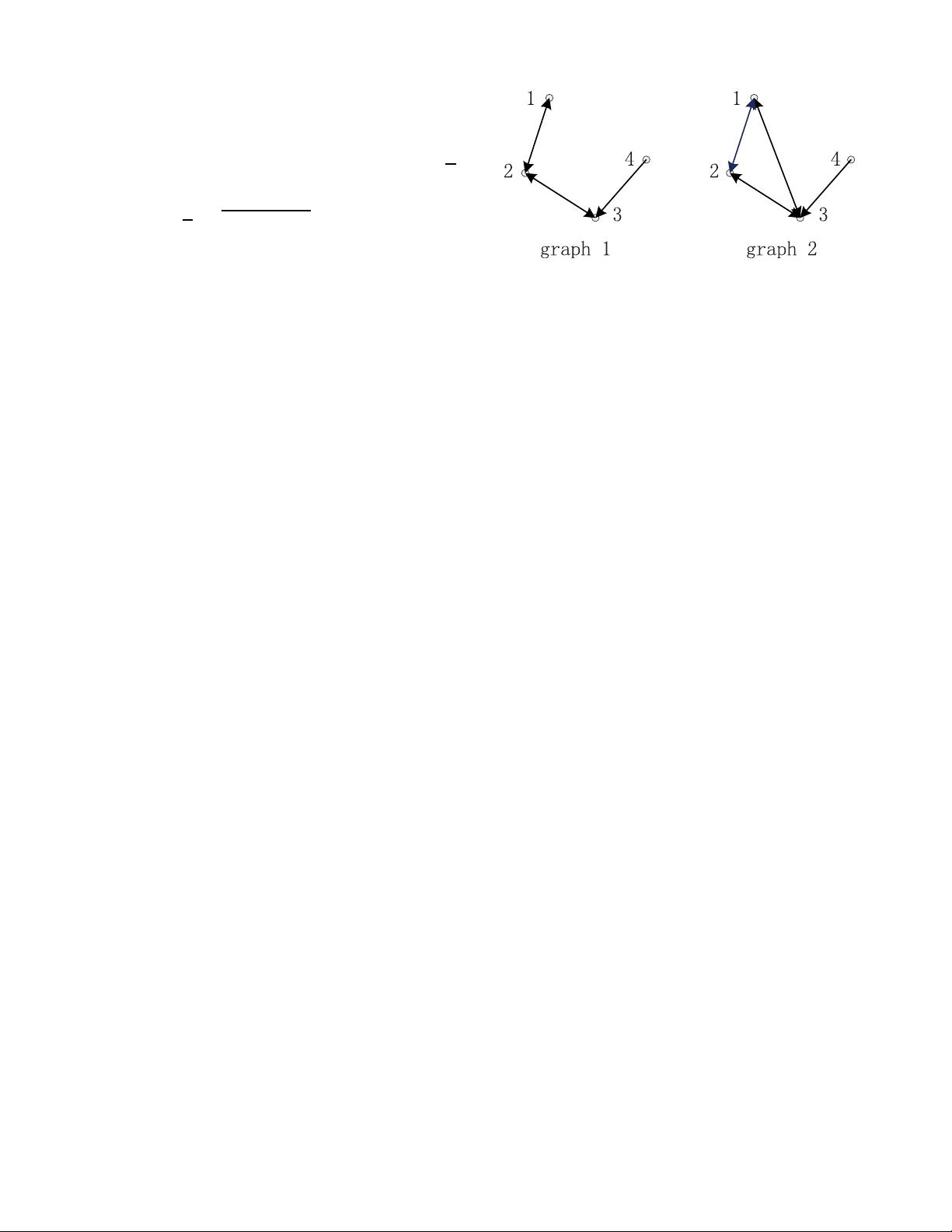
Fig. 1. Markovian jump coupling.

condition of the ith neural networks. For example, we consider

a random coupling, which jumps between two states, as shown

in Fig. 1 (i.e., graph 1 and graph 2), where nodes 2 and

4 have the same neighbors for both cases, which means

(α(k)) = 1fori = 2, 4. However, for nodes 1 and 3, the

neighbors are varying with α(k),thatis,ϑ

(α(k)) ∈{1, 2}

for i = 1, 3.

Remark 3: For the coupled systems (i.e., distributed sys-

tems, multiagent systems, and complex networks), the con-

nections among the nodes are always unreliable caused by the

communication constraints, such as packet dropouts, transmis-

sion delays, and so on. This phenomenon motivates people

to study the time-varying connection for coupled systems,

and the Markovian jump coupling is a classic one. In [45],

the coupling-independent controller has been proposed. How-

ever, for Markovian jump systems, how to make full use of

the Markov chain information to design a less conservative

estimator is an important issue. Note that each node cannot

obtain entire coupling information. Thus, a new structure

estimator called local coupling structure-dependent estimator

is presented, where the parameters of the estimator depend on

the local coupling structure.

C. Estimation Error System

Coupled neural networks with randomly occurring distrib-

uted delays (1) can be rewritten as the following augmented

form:

⎧

⎪

⎨

⎪

⎩

x(k + 1) = (

A(θ) + W

α(k)

⊗ )x(k) +

B(θ)G(x(k))

+β

F(θ )

+∞



d=1

G(x(k − d)) +

E(θ )v(k)



i=1

(β

(k) − β

)



F(θ )

+∞



d=1

G(x(k − d))



y(k) =

C(θ)x(k) +

D(θ)v(k)

z(k) =

L(θ )x(k)

(8)

where

x(k) =[x

(k)

... x

(k)

]

y(k) =[y

(k)

... y

(k)

]

z(k) =[z

(k)

... z

(k)

]

G(x(k)) =[g(x

(k))

g(x

(k))

... g(x

(k))

]

剩余10页未读，继续阅读

weixin_38750644

粉丝: 5
资源: 907

鲁棒估计：随机分布时滞与马尔可夫跳跃耦合神经网络

时变时滞马尔可夫跳跃神经网络的鲁棒指数稳定性

具有变时滞和马尔可夫切换的随机递归神经网络的弱收敛(英文).pdf

具有依赖于模式的时变时滞和马尔可夫跳跃的Cohen-Grossberg神经网络的鲁棒收敛

具有随机扰动的中立型马尔可夫跳跃脉冲时滞神经网络的新型鲁棒指数稳定性

时滞离散马尔可夫跳跃系统的鲁棒故障检测 (2006年)

分布时滞马尔可夫跳跃系统的无偏估计

具有分布时滞和马尔可夫参数的双向联想记忆神经网络的随机渐近稳定性 (2013年)

具有马尔可夫切换和时变混合时滞的脉冲随机神经网络的鲁棒指数稳定性

基于耗散的具有跳跃衰落信道的马尔可夫跳跃神经网络异步状态估计

一类具有时滞和不确定性的离散随机马尔可夫跳跃系统的时滞相关鲁棒稳定性

最新资源