图论基础与应用：连通性、遍历与拓扑排序

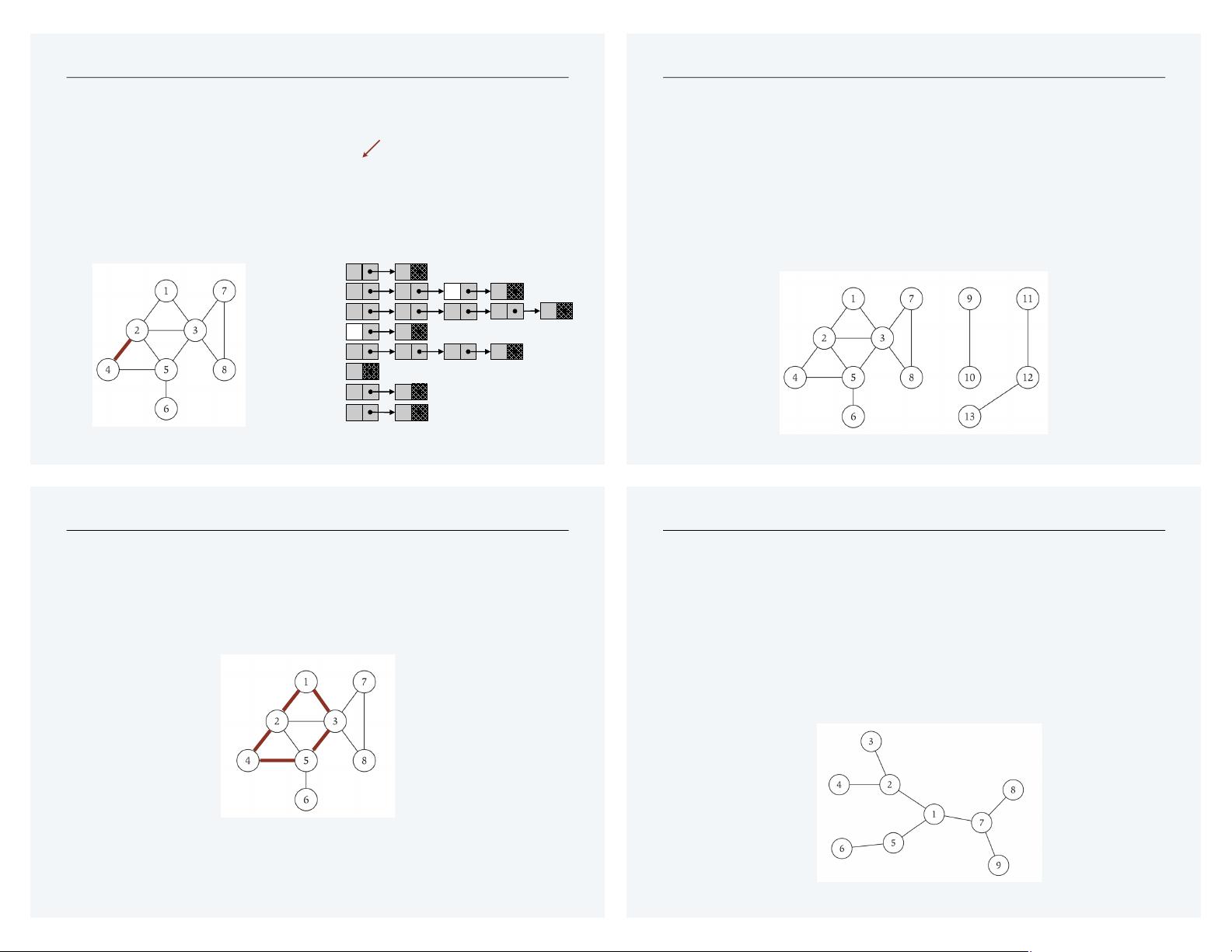
"这篇文档是关于图论在算法设计中的应用，主要涵盖了基本定义、图的连通性、图的遍历、二分图检测、有向无环图（DAG）及其拓扑排序等内容。" 在计算机科学中，图论是一种强大的工具，广泛应用于算法设计，它用于建模对象之间的关系。文档首先介绍了图的基本概念，包括无向图的定义。一个无向图（G）由节点（或顶点）集合V和边（或弧）集合E组成。例如，V={1,2,3,4,5,6,7,8}表示8个节点，E={1-2,1-3,2-3,2-4,2-5,3-5,3-7,3-8,4-5,5-6,7-8}表示11条边。节点代表对象，边则表示这些对象之间的关系。图的大小通常用参数n（节点数）和m（边数）来衡量，在这个例子中，n=8，m=11。 图的连通性和遍历是图论中的关键概念。连通性指的是图中任意两个节点之间都存在路径。对于无向图，可以通过遍历算法，如深度优先搜索（DFS）或广度优先搜索（BFS），来判断图是否连通。这些算法有助于理解图的结构，并在寻找特定路径或组件时非常有用。 文档还提到了二分图测试，这是图论中的一个重要问题。二分图是图的一个子集，其中所有节点可以被分成两个互不相交的集合，且每条边连接不同集合的节点。检测一个图是否为二分图有多种方法，例如通过颜色编码或Kosaraju-Sharir算法。二分图在解决配对问题、网络流和某些优化问题中具有重要作用。 在有向图中，连通性可能更为复杂。有向图的边具有方向，因此可能存在无法从一个节点到达另一个节点的情况。在这种情况下，强连通性是指图中每个节点都能到达其他所有节点，而弱连通性仅要求通过反向边可达。有向无环图（DAG）是一类特殊的有向图，不存在环路，它们在任务调度、依赖分析和时间顺序建模等方面有广泛应用。 最后，文档提到了拓扑排序，这是DAG特有的概念。拓扑排序是将DAG的节点排列成线性序列，使得图中每条有向边从序列前的节点指向序列后的节点。有多种方法实现拓扑排序，如Kahn的算法，它通过找到没有前驱（入度为0）的节点并将其移除，直到所有节点都被处理。 图论在实际问题中的应用广泛，如邮件网络分析（如一周的Enron邮件）、政策影响研究（如FCC游说联盟的演变）和社会现象建模（如肥胖症在社会网络中的传播）。这些示例表明，理解和运用图论的算法能够帮助我们更好地理解和解决现实世界的问题。