线性代数图解：矩阵分解的艺术

“The Art of Linear Algebra中文版，一本旨在通过图形化解释使线性代数易懂的书籍，由Kenji Hiranabe创作，并得到Gilbert Strang的支持。书中涵盖矩阵分解、高斯消去法、格拉姆-施密特正交化、特征值与对角化以及奇异值分解等核心概念。” 线性代数是现代数学、物理、工程和计算机科学等领域不可或缺的基础工具。这本书《The Art of Linear Algebra》特别注重将抽象的线性代数概念以图形化的方式呈现，使得初学者也能轻松理解和掌握。 1. **理解矩阵** - 书中提供了四个不同的视角来解析矩阵，帮助读者从不同层面把握矩阵的本质。这四个视角可能包括矩阵的几何表示、运算性质、行列式以及它们在实际问题中的应用。 2. **向量乘以向量** - 向量的乘法通常涉及点积（内积）和叉积（外积），书中通过两个视角展示了这些概念，帮助读者理解向量之间的相互作用和几何意义。 3. **矩阵乘以向量** - 这部分探讨了矩阵与向量的乘法，揭示了线性变换的原理。矩阵乘法可以表示为将一个向量投射到不同的空间方向上，或者通过线性组合改变向量的形状。 4. **矩阵乘以矩阵** - 书中用四个视角深入解释矩阵乘法，这不仅涉及数值计算，还揭示了矩阵乘法如何表示复合变换和线性映射。 5. **实用模式** - 作者介绍了线性代数在实际问题中的应用，如数据处理、图像分析和控制系统设计等，让理论知识与实践相结合。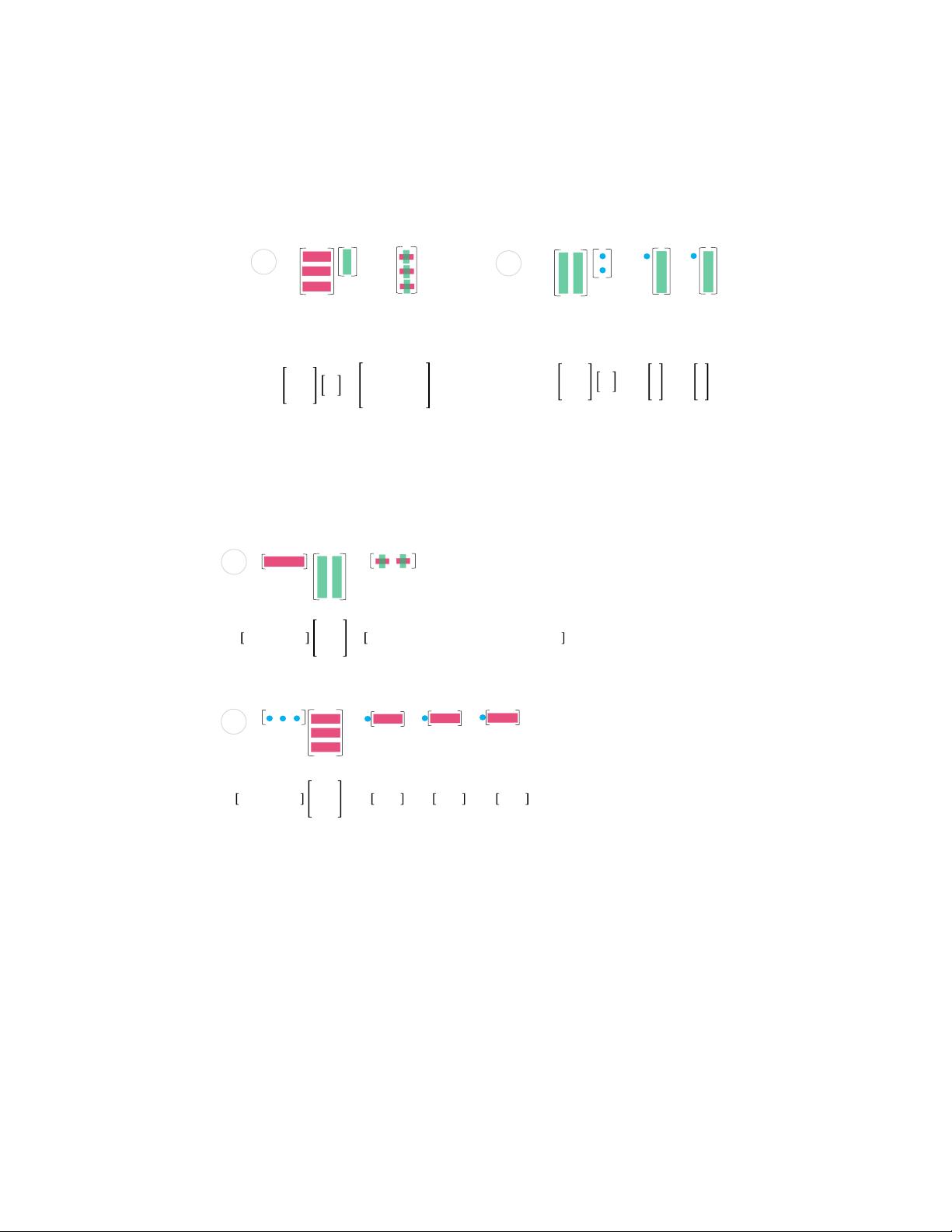 6. **矩阵的五种分解** - 矩阵分解是线性代数的核心，包括： - **CR分解**（Column-Row Decomposition）：矩阵可以表示为列向量的线性组合。 - **LU分解**（Gaussian Elimination, LU）：通过高斯消去法将矩阵分解为一个下三角矩阵和一个上三角矩阵，方便求解线性方程组。 - **QR分解**（Gram-Schmidt Orthogonalization, QR）：将矩阵转化为正交矩阵和上三角矩阵，用于处理非方阵或进行数值稳定计算。 - **特征值与对角化**（Eigenvalues and Diagonalization, QΛQT）：矩阵可以表示为其特征向量的集合和对应特征值的对角矩阵，揭示了矩阵的固有性质。 - **奇异值分解**（Singular Value Decomposition, UΣVT）：将任意矩阵分解为两个酉矩阵和一个对角矩阵，是处理稀疏数据、图像压缩和机器学习等领域的基础。 这本书通过可视化的方法，让复杂的线性代数概念变得直观易懂，无论是初学者还是专业人士，都能从中受益。结合Gilbert Strang的评价，我们可以看出这本书的独特价值在于将线性代数的抽象概念转化为视觉盛宴，让学习变得更加生动有趣。