基于因子图的下行MIMO-SCMA迭代接收器：消息传递和分布式协作检测
195 浏览量
更新于2024-07-14
收藏 2.09MB PDF 举报
下行MIMO-SCMA迭代接收器：消息传递和分布式协作检测
下行MIMO-SCMA系统是当前无线通信领域的研究热点之一，especially in the context of 5G and beyond wireless networks. 在这种系统中，多个用户共享相同的频带宽，通过sparse code multiple access (SCMA)技术来实现多用户接入。但是，随着用户数量、天线数量和信道长度的增加，检测复杂度指数增长，以至于传统的检测方法无法满足实际应用的需求。
为了解决这个问题，本文提出了一种基于因子图的近似Optimal低复杂度迭代接收器。该方法通过引入辅助变量，构建了一个拉伸的因子图，然后使用消息传递算法实现检测。这种方法可以大大减少检测的复杂度，同时保持了较高的检测性能。
在下行MIMO-SCMA系统中，检测算法的设计是一个关键问题。传统的检测方法，如Maximum Likelihood (ML)检测和Minimum Mean Square Error (MMSE)检测，虽然可以实现 Optimal检测，但是其复杂度随着用户数量、天线数量和信道长度的增加而指数增长。为了解决这个问题，需要设计一种低复杂度的检测算法。
基于因子图的迭代接收器是近年来发展的一种检测技术，该方法可以将检测问题转化为一个概率推断问题，然后使用消息传递算法来求解。这种方法可以大大减少检测的复杂度，同时保持了较高的检测性能。
在本文中，我们首先介绍了下行MIMO-SCMA系统的基本原理，然后讨论了基于因子图的迭代接收器的设计方法。最后，我们通过仿真实验验证了该方法的有效性。
在实际应用中，下行MIMO-SCMA系统可以广泛应用于各种无线通信场景，如5G和beyond wireless networks、物联网、vehicular networks等。这种系统可以提供高效的无线通信服务，满足未来通信的需求。
本文提出了一种基于因子图的近似Optimal低复杂度迭代接收器，解决了下行MIMO-SCMA系统中的检测问题。该方法可以大大减少检测的复杂度，同时保持了较高的检测性能，为未来无线通信的发展奠定了基础。
知识点：
1. 下行MIMO-SCMA系统的基本原理
2. 基于因子图的迭代接收器的设计方法
3. 消息传递算法的原理和应用
4. 下行MIMO-SCMA系统中的检测问题
5. 低复杂度检测算法的设计方法
6. 基于因子图的迭代接收器在下行MIMO-SCMA系统中的应用
7. 下行MIMO-SCMA系统在未来无线通信中的应用前景
3446 IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 17, NO. 5, MAY 2018
Finally, the proposed algorithms are evaluated via Monte Carlo
simulations. The results demonstrate the superior performance
of the proposed message passing receivers for MIMO-SCMA
system and also show the great potentials of using cooperative
detection.
The remainder of this paper is organized as fol-
lows. In Section II, the system model of the consid-
ered MIMO-SCMA is introduced. Section III develops a
low-complexity receiver based on stretched factor graph.
In Section IV, we propose a convergence-guaranteed receiver
by convexifying the Bethe free energy. Two distributed coop-
erative detection methods are investigated in Section V. Simu-
lation results are shown and discussed in Section VI. Finally,
conclusions are drawn in Section VII.
Notations: We use a boldface letter to denote a vector.
The superscript T and −1 denote the transpose and the
inverse operations, respectively; N denotes the neighboring
set of a variable or a function; G(m
x
,v
x
) denotes a Gaussian
distribution of variable x with mean m
x
and variance v
x
; |·|
denotes the modulus of a complex number or the cardinality
of a set; ·
2
denotes the
2
norm; ∝ represents equality up
to a constant normalization factor; x\x denotes all variables
in x except x.
II. P
ROBLEM FORMULATION
A. System Model
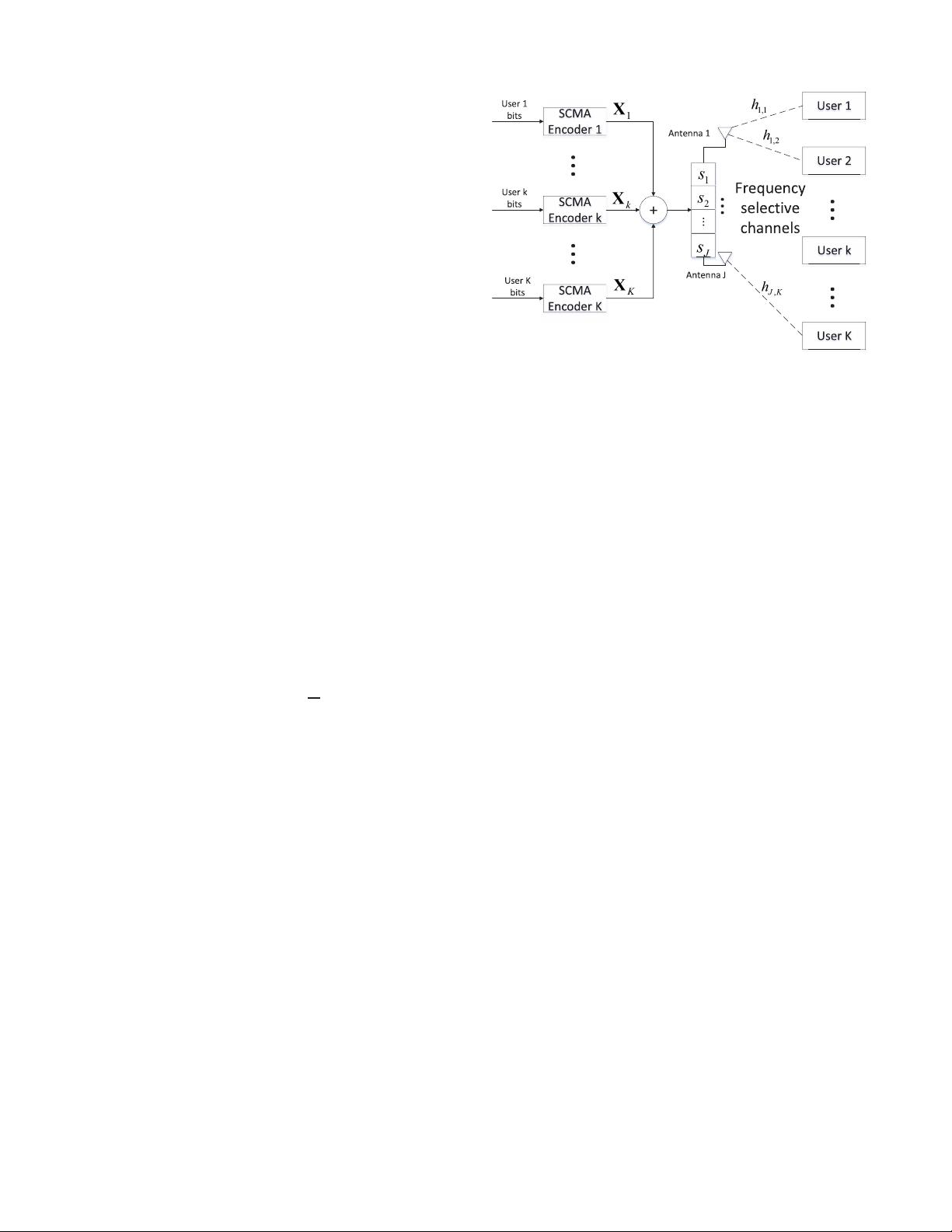
We consider a K-user downlink MIMO-SCMA system,
where each user is equipped with a single antenna and the base
station is equipped with J transmit antennas. In the orthogonal
multiple access scenario, we usually set K ≤ J to avoid inter-
user interferences. In the non-orthogonal scenario, K can be
greater than J and we define =
K
J
as overloading factor.
The SCMA encoder is a mapping function that maps every
log
2
M coded bits to an J-dimensional SCMA codeword. The
codewords are selected from a user-specific SCMA codebook
of size M .Letx
n
k
=[x
n
k,1
,...,x
n
k,J
]
T
be the transmitted
codeword of user k at time instant n, which is a sparse vector
with D<Jnonzero entries. Then the codewords can be
multiplexed over J transmit antennas at the base station. The
block diagram of the considered system is illustrated in Fig. 1.
Let’s denote the transmitted symbol at the jth antenna and
time instant n by s
n
j
,thens
n
j
is given by
s
n
j
=
K
k=1
x
n
k,j
. (1)
In order to capture the sparse feature of SCMA, a binary
indicator vector f
k
is introduced for user k,wherethejth
element in f
k
is given by
f
k,j
=
0 x
k,j
=0
1 x
k,j
=0.
(2)
The indicate matrix is given as F =[f
1
,...,f
K
],wherethe
nonzero entries in the jth row denote the conflicting users over
the jth antenna while the nonzero entries in the kth column
indicate the resources occupied by user k.
Fig. 1. System model for downlink MIMO-SCMA.
The signal from base station transmits over frequency selec-
tive fading channels with L taps and is received at different
users. With the assumption of perfect synchronization between
the base station and users, the received signal at user k and
time instant n can be further written as
y
n
k
=
J
j=1
L−1
l=0
h
l
j,k
s
n−l
j
+ ω
n
k
, (3)
where h
l
j,k
is the lth tap coefficient of the multipath channel
between the jth antenna and kth user, and ω
n
k
is additive white
Gaussian noise (AWGN) at time instant n with power spectral
density N
0
.
B. Probabilistic Model
Assuming that N codewords are transmitted, we further
denote X
k
and y
k
as transmitted SCMA codewords and
received signal samples of the kth user, and X as the trans-
mitted symbols of all users. Assuming perfect channel state
information, each user can perform the optimal maximum a
posteriori (MAP) detection based on measurement y
k
,which
can be expressed as
ˆ
X
k
=argmax
X
k
p(X
k
|y
k
)
=argmax
X
k
p(X|y
k
)dX\X
k
. (4)
Following Bayesian rules, p(X|y
k
) reads
p(X|y
k
) ∝ p(X)p(y
k
|X) (5)
where p(X) is the joint aprioridistribution and p(y
k
|X) is
the joint likelihood function. Since all transmitted symbols are
assumed independent, we have p(X)=
j,k,n
p(x
n
k,j
),where
p(x
n
k,j
) is calculated based on the log likelihood ratios (LLRs)
of coded bits from the output of channel decoder.
The computational complexity of the optimal MAP receiver
in (4) increases exponentially with the product of the number
of users, the number of antennas and the channel length.
In the following, we develop low-complexity message passing
receivers for MIMO-SCMA system.
剩余14页未读，继续阅读
2022-11-28 上传
1569 浏览量
2021-05-31 上传
117 浏览量
178 浏览量
点击了解资源详情
点击了解资源详情
244 浏览量
点击了解资源详情
weixin_38665093
- 粉丝: 10
- 资源: 931
我的内容管理
展开
最新资源
- jquery开关按钮基于Bootstrap开关按钮特效
- merkle-react-client:客户
- 财务管理系统javaweb项目
- DOM-Parsing:DOM解析和序列化
- FastReport v6.7.11 Enterprise installer .zip
- pid控制器代码matlab-AutomatedBalancingRobot:自动平衡机器人是一个项目，其中建造了一个两轮机器人，并将其编程为
- 基于MATLAB模型设计的FPGA开发与实现.zip_UBK_matlab与fpga_simulink模型_struck9hw_
- ubiq：基于HugSQL和GraphQL的Web应用程序，移动部分最少
- 行业文档-设计装置-一种折叠式防滑书立.zip
- 意法半导体参考文献及软件资料.7z
- LoRa-High-Altitude-Balloon:这是蒙大拿州立大学LoRa小组顶峰项目的存储库，该项目是蒙大纳州太空资助财团BOREALIS实验室的项目。 以下代码在定制板上运行，该定制板上旨在收集高空气球有效载荷上的大气数据
- BW_Anal-开源
- nuaa_check_action:inuaa打卡，基于GitHub Action的南航校内，校外打卡
- alex_presso
- perf:PERF是详尽的重复查找器
- 行业文档-设计装置-一种折叠式包装纸箱.zip
