弱耦合Rossler振子的广义扩展相周期态及其耦合势理论

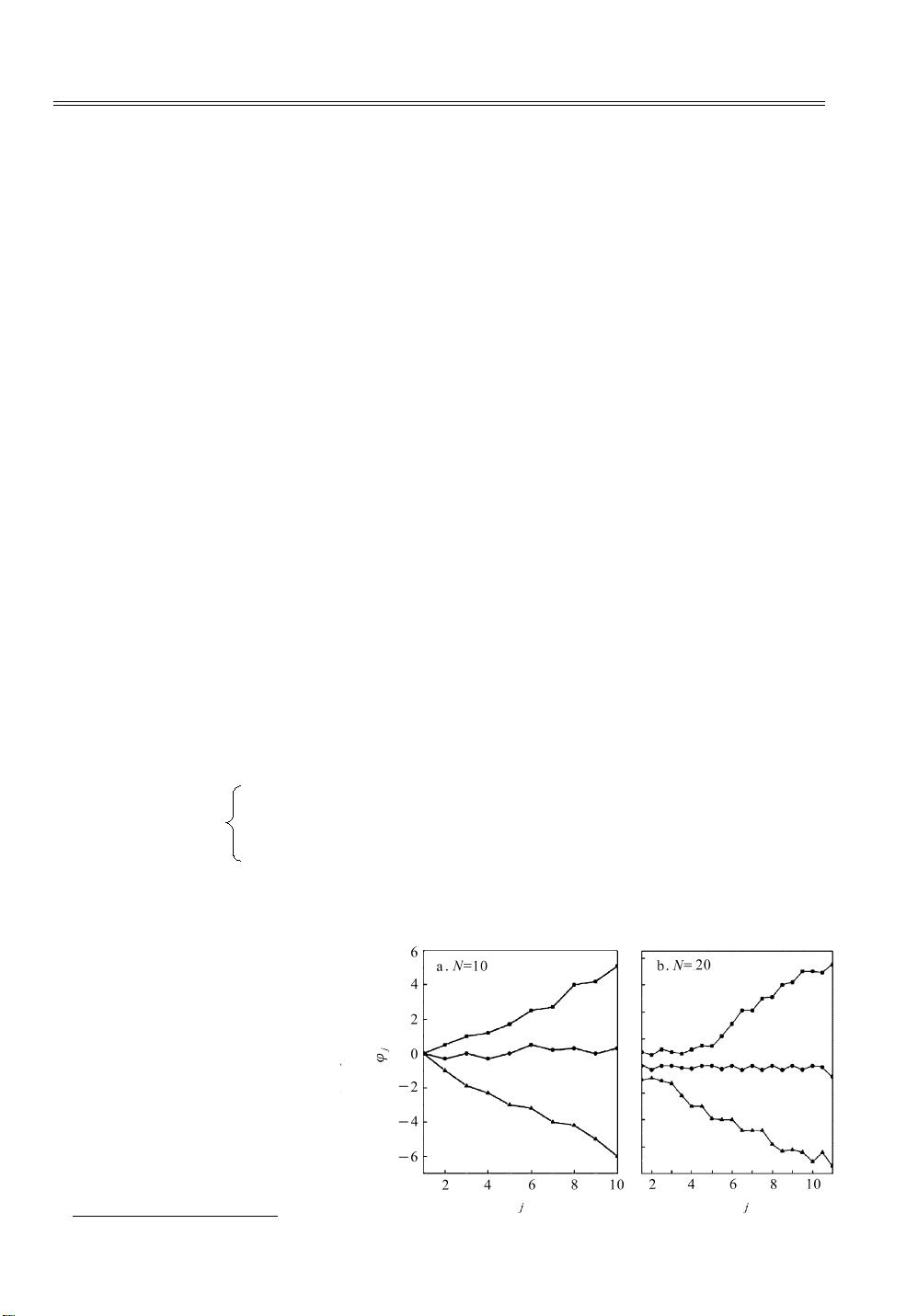
本文主要探讨了2002年发表的《弱耦合Rossler振子中广义扩展相的周期态》论文，该研究由吕华平、何岱海、高建和胡岗等人合作完成，发表于北京师范大学学报（自然科学版）。论文的核心内容是提出并定义了一个新的概念——耦合势（Coupling Potential, H(τ)），这是一种用于描述耦合系统中扩展相位分布的有效工具。在文中，研究人员以经典的Rossler振子模型为研究对象，该模型在无耦合情况下表现出混沌行为。 他们发现，在弱耦合条件下，Rossler振子系统呈现出广义扩展相态，即尽管所有振子的轨道相同，但不同振子之间的相位之间存在函数关系。这种状态下的动力学特性与大耦合强度下的同步态有所不同，后者分为同相态和扩展态。文章指出，通过计算H(τ)的值，尤其是其在τ=0处的位置，可以准确预测格子同步态（Grid Synchronization Phase State, GSPS）的不同形式。H(τ)的局部极小值对应着所有振子相位接近一致，而接近但不等于极小值的情况则决定了振子沿周期轨道的分布方向。 论文的关键词包括超混沌、时空结构和弱耦合，强调了在弱耦合状态下，系统动力学性质的变化以及其可能带来的秩序化周期状态。研究者还引用了近年来关于时空系统混沌和斑图的研究成果，这些工作为理解耦合振子在不同耦合强度下的行为提供了理论基础。 文章最后给出了Rossler振子的具体数学模型，其中包含控制参数a、b、c和ω，以及它们对系统动态的影响。通过对这些参数的调整，研究者展示了如何通过控制耦合来实现对广义扩展相态的调控，这在理论上对于理解其他复杂系统的行为具有普遍性意义。 这篇论文不仅提供了对弱耦合Rossler振子的新见解，而且提出的方法和技术也为深入探究耦合系统中的相位动力学和时空结构提供了一种实用工具，对后续的混沌系统研究有着重要价值。