MATLAB实现静电场边值问题的有限差分法

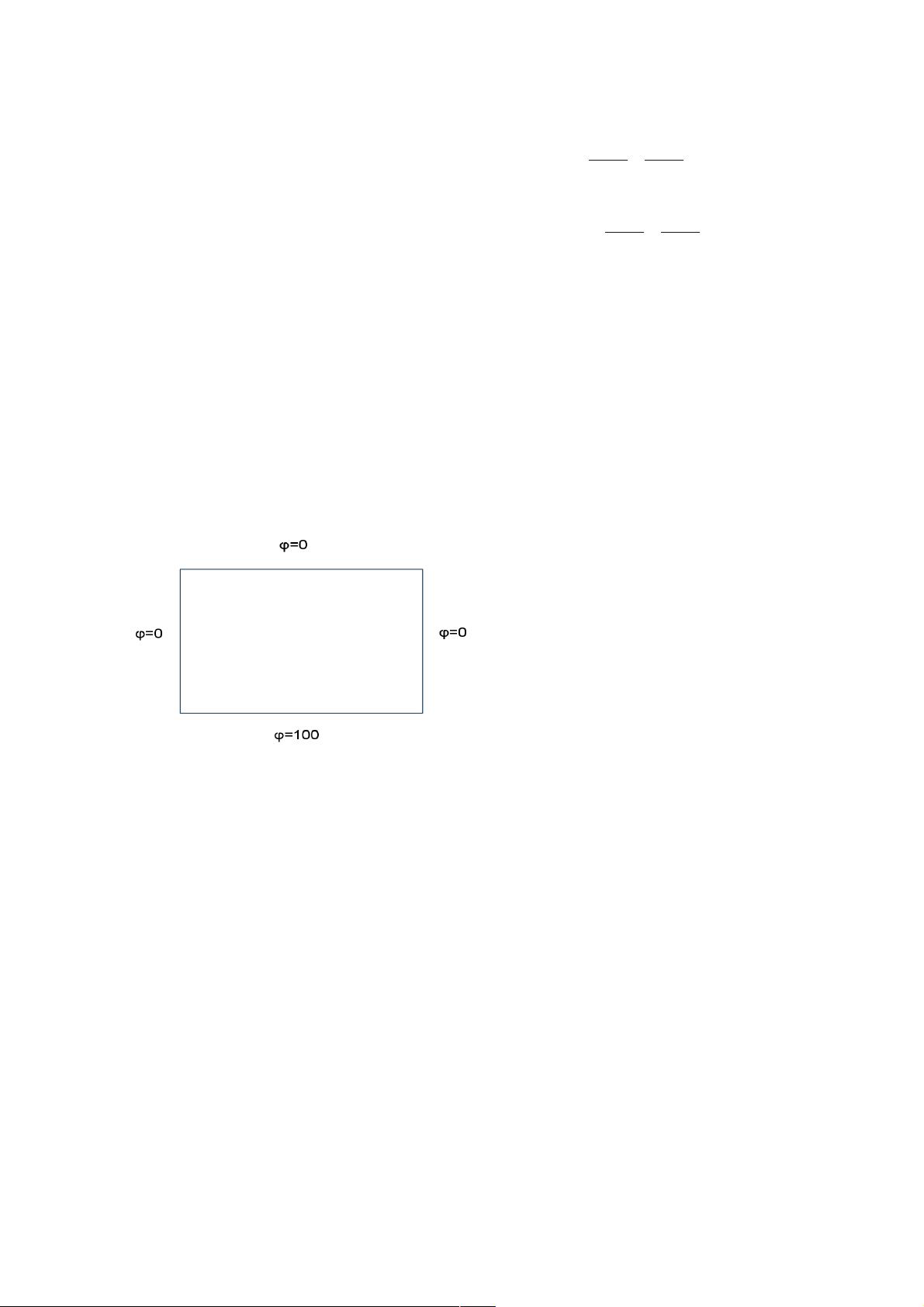
"静电场边值问题的编程仿真主要利用MATLAB进行有限差分法的算法实现，通过将偏微分方程转化为线性方程组并应用迭代法求解。文章探讨了如何优化迭代法以及解决闪电模拟问题，对原有模型进行改进。" 静电场边值问题通常涉及到泊松方程或拉普拉斯方程，这些是经典场理论中的基本方程。然而，由于解偏微分方程的复杂性，实际操作中往往需要寻求数值解。有限差分法是一种有效的数值方法，它通过将连续变量离散化来近似微分。 有限差分法的基本思想是用差商来近似导数。例如，一阶差分可以表示为f'(x) ≈ (f(x+h) - f(x))/h，随着h趋近于0，这个差分逼近导数的定义。二阶差分用于近似二阶导数，如f''(x) ≈ (f(x+h) - 2f(x) + f(x-h))/(h^2)，这是在误差控制和稳定性方面更为精确的近似。 在静电场问题中，泊松方程表述为∇^2U = ρ，其中∇^2是拉普拉斯算子，U是电势，ρ是电荷密度。采用二阶差分，可以将拉普拉斯算子替换为有限差分的形式，例如在三维情况下，对每个坐标轴应用二阶差分，得到一个关于U的离散方程。 在MATLAB编程环境中，可以使用二维或三维网格来划分空间，然后利用矩阵操作来存储和处理这些离散化的数据。通过设置步长h=k=l=1，可以将泊松方程转化为一个大的线性系统。例如，对于均匀网格，有限差分形式的泊松方程可以写为关于U的线性方程组，每个点的电势U(i,j,k)受其周围六个点的影响。 为了求解这个线性方程组，可以使用迭代法，如高斯-塞德尔迭代法或雅可比迭代法。迭代法的选择和优化涉及收敛速度、稳定性和计算效率。优化迭代法可能包括预条件技术、线搜索策略或自适应步长控制等策略，以提高计算效率并确保收敛。 在文章中提到，作者应用这种方法解决了闪电模拟问题，使用更优化的算法重新计算并改进了原有模型。此外，作者还讨论了与之前研究不同的观点，可能涉及到模型的改进、边界条件的处理或其他数值方法的应用。 静电场边值问题的编程仿真利用MATLAB和有限差分法，提供了一种数值解的方法。通过迭代法求解线性方程组，可以有效地逼近实际问题的解，并允许对模型进行调整和优化，以更好地匹配物理现象。这种技术广泛应用于物理学、工程学和其他领域，解决复杂的偏微分方程问题。