Sardinas-Patterson算法实现唯一可译码判断

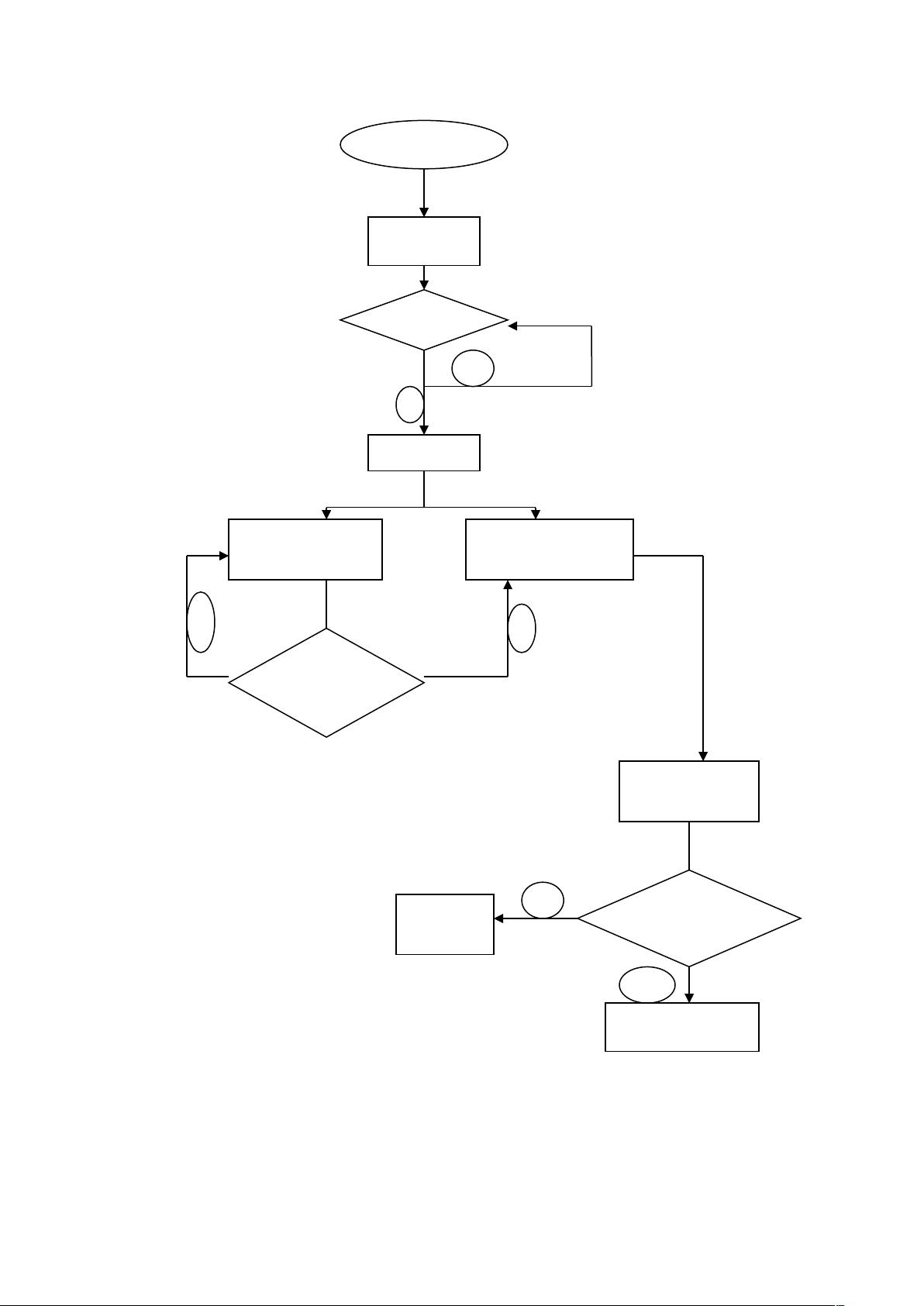
"唯一可译码的判决程序设计与实现" 唯一可译码是指在通信编码中，一种编码方式使得任何两个不同的合法码字没有公共前缀，这样的编码可以确保接收端无歧义地解码。唯一可译码在信息传输中具有重要意义，因为它避免了错误的解码可能性。在本实验中，我们将使用Sardinas-Patterson算法来判断给定的一组码字是否构成唯一可译码。 实验内容涉及编程实现Sardinas-Patterson算法，该算法主要用于判断一组码字集是否满足唯一可译码条件。实验环境要求包括计算机、Windows操作系统以及VC++6.0作为编程工具，目的是让学生熟悉唯一可译码的判决准则，掌握C语言编程技巧，特别是字符串处理。 实验原理基于唯一可译码的判决准则，具体算法流程如下： 1. 检查所有码字的长度，将码字按长度升序排列。 2. 对于每一对长度相同的码字，检查它们是否完全相同。如果不同，那么它们不能有公共前缀。 3. 如果某个码字是另一个码字的前缀，将其后缀加入新的集合Xn。 4. 遍历剩余的码字，如果发现有码字是Xn中的任何一个码字的前缀，那么码字集不构成唯一可译码，否则为唯一可译码。 实验设计的关键算法包括： a. 前缀判断函数`qian(signa, signb)`：比较两个码字是否具有相同的前缀。如果码字长度不同，先调整长度较大的码字为较小的。然后逐位比较，如果所有位都相同，返回1表示有前缀关系；否则返回0。 b. 后缀求取函数`signSub(signa, signb)`：当码字Wi是码字Wj的前缀时，提取Wi之后的部分作为后缀d。如果长度不同，将Wj的后部分添加到新结构体d中。 c. 检查剩余码字中是否有Xn集合的前缀的函数`cmp1()`：遍历所有码字对，找出前缀关系，并将后缀存入Xn集合，如果发现存在Xn中的前缀，表明不满足唯一可译码条件。 实验要求学生在预习实验原理的基础上，高效地完成编程任务，同时在实验过程中遵守实验室规则并认真填写实验报告。通过本次实验，学生不仅能深入理解唯一可译码的理论，还能提升实际编程能力，特别是在字符串处理方面的实践技能。