Mathematica中的微积分操作：极限与微分

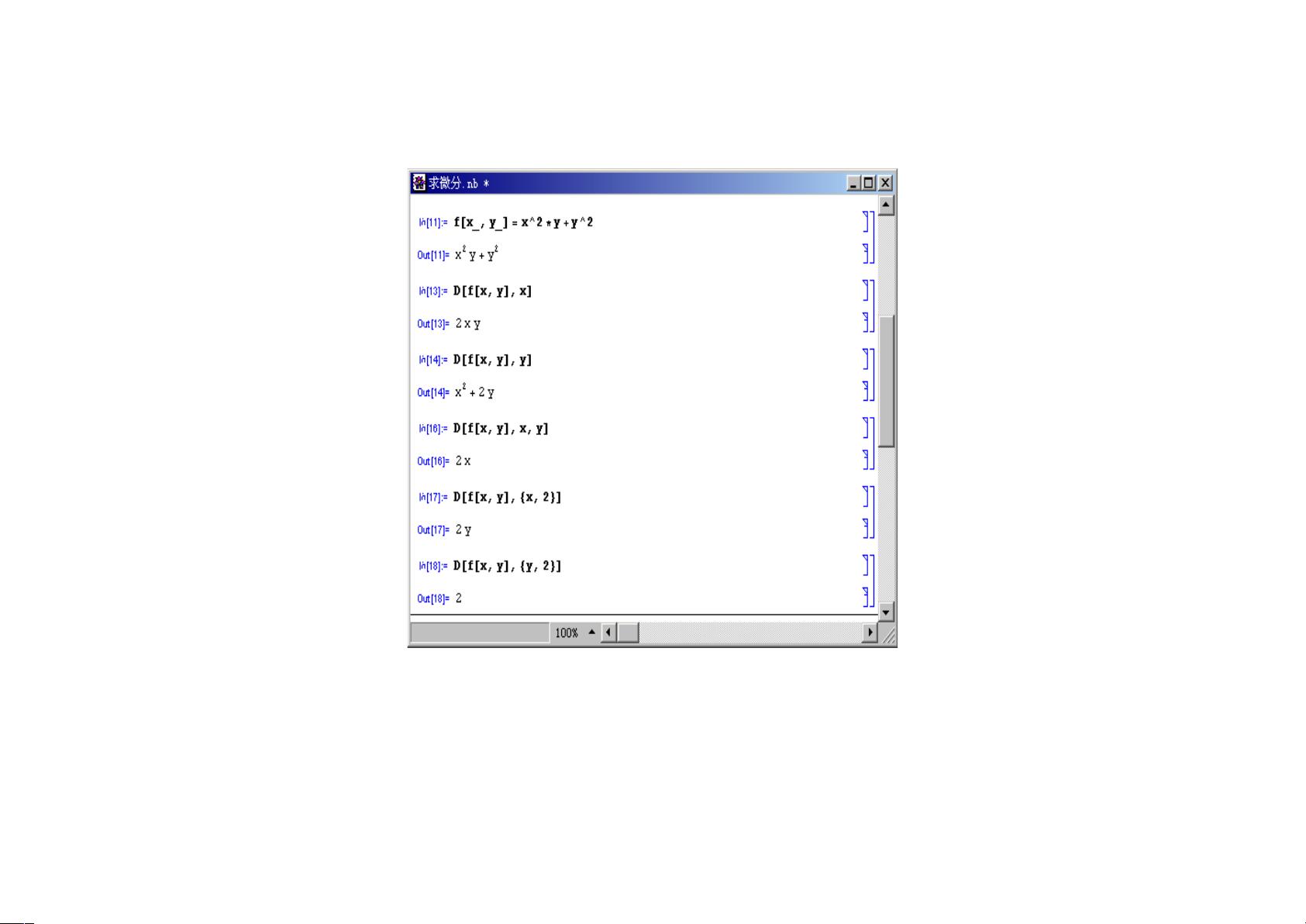
"本章介绍了微积分的基本操作，包括如何使用Mathematica进行极限计算和微分计算。极限部分详细讲解了Limit命令的用法，包括求解常数、正无穷和负无穷的极限，以及左右极限。微分部分则阐述了D命令的功能，如求函数的一阶、高阶导数，偏导数，以及全微分，并举例说明了含未知函数的微分和链式法则的应用。" 在微积分中，极限是一个基本概念，用于描述函数在某一点附近的行为。Mathematica提供了Limit命令来计算极限。例如，`Limit[expr,x->x0]`用于计算当x趋近于x0时expr的极限。如果需要求解左极限和右极限，可以分别使用`Limit[expr,x->x0,Direction->1]`和`Limit[expr,x->x0,Direction->-1]`。这些命令允许我们处理各种类型的极限问题，包括当x趋向于常数或无穷大时的情况。 微分是微积分的另一核心概念，它涉及函数的局部变化率。在Mathematica中，我们可以使用D命令来求导数。例如，`D[f,x]`用于计算函数f关于x的一阶导数，`D[f,x1,x2,…]`用于计算多元函数的偏导数，而`D[f,{x,n}]`则用于求n阶导数。此外，`D[f,x,NonConstants->{v1,v2,----}]`可以计算那些不随x变化的变量v1, v2等的导数。通过实例，我们看到D命令可以用来求解sin(x)的一阶导数、e^xsin(x)的二阶导数，以及对sin(ax)求导，甚至对二元函数f(x,y)=x^2*y+y^2求一阶和二阶偏导。 对于函数的全微分，Mathematica的Dt命令可以帮助我们得到包含所有变量依赖关系的微分表达式。`Dt[f]`和`Dt[f,x]`分别用于求函数f的整体微分和关于x的偏全微分。全微分在处理多元函数时特别有用，因为它考虑了所有变量之间的相互影响。 通过Mathematica，我们可以高效准确地进行微积分运算，这对于理解和应用微积分理论至关重要。无论是分析函数的局部行为，还是研究函数的变化规律，这些工具都能提供强大的支持。在实际问题中，比如物理学、工程学和经济学等领域，微积分的这些操作都有广泛的应用。