计算机图形学:直线与椭圆算法详解及裁剪技术
159 浏览量
更新于2024-06-24
收藏 2.75MB DOC 举报
本篇文档是关于计算机图形学课程设计的毕业论文,主要探讨了直线段生成算法、椭圆Bresenham生成算法、直线段裁剪算法以及图形求交技术。论文以理学院计算数学专业学生LH的名义撰写,完成于2010年12月31日。
首先,论文详细介绍了几种常用的直线生成算法,包括:
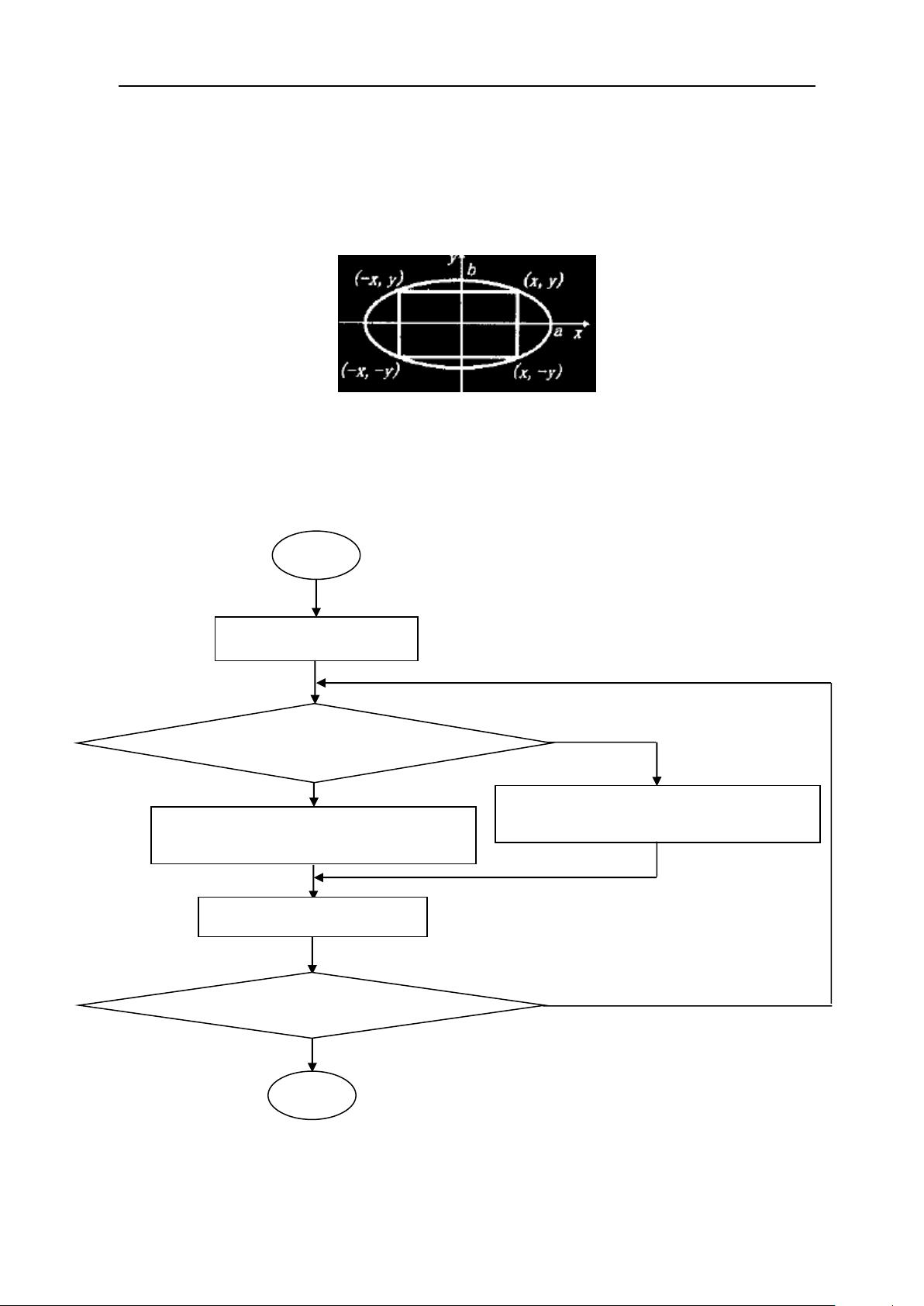
1. **DDA(数字微分分析器)方法**:这是一种基于梯形近似的基本算法,它通过逐像素移动并计算增量来生成直线。1.1.1部分阐述了算法原理,1.1.2描述了实现步骤,附有伪程序和流程图。
2. **Bresenham算法**:这是一种更精确的算法,通过判断当前点与目标点的偏移方向决定步进方式,减少误差。1.2节深入剖析了Bresenham算法,包括原理、步骤、程序描述和流程图。
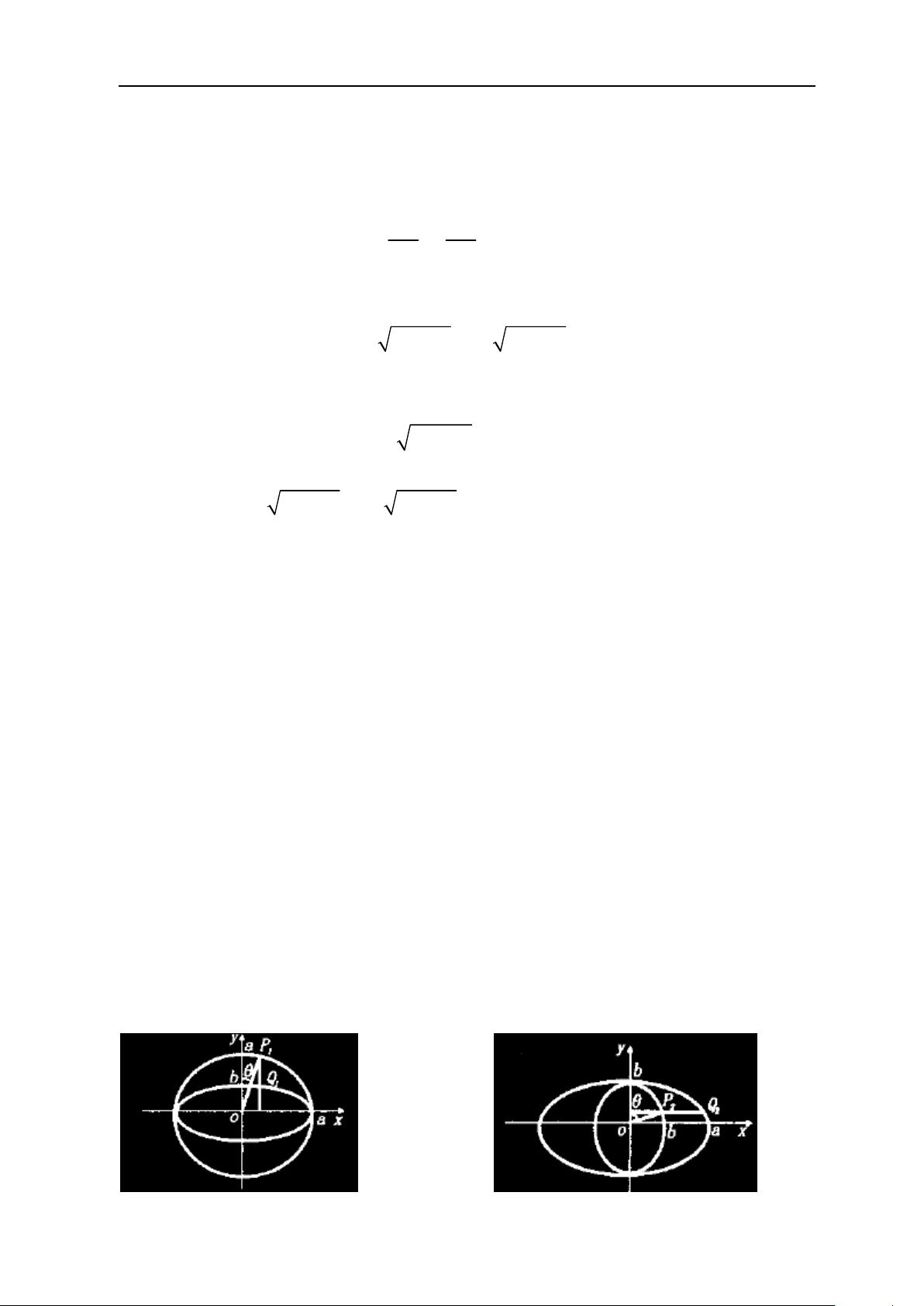
接着,论文扩展到曲线生成,如**椭圆的Bresenham生成算法**,涉及椭圆的曲率分析、方程解析及具体生成流程。1.3~2.3部分分别讨论了算法的实现过程、流程图和程序描述。
直线段裁剪算法是另一个关键部分,包括:
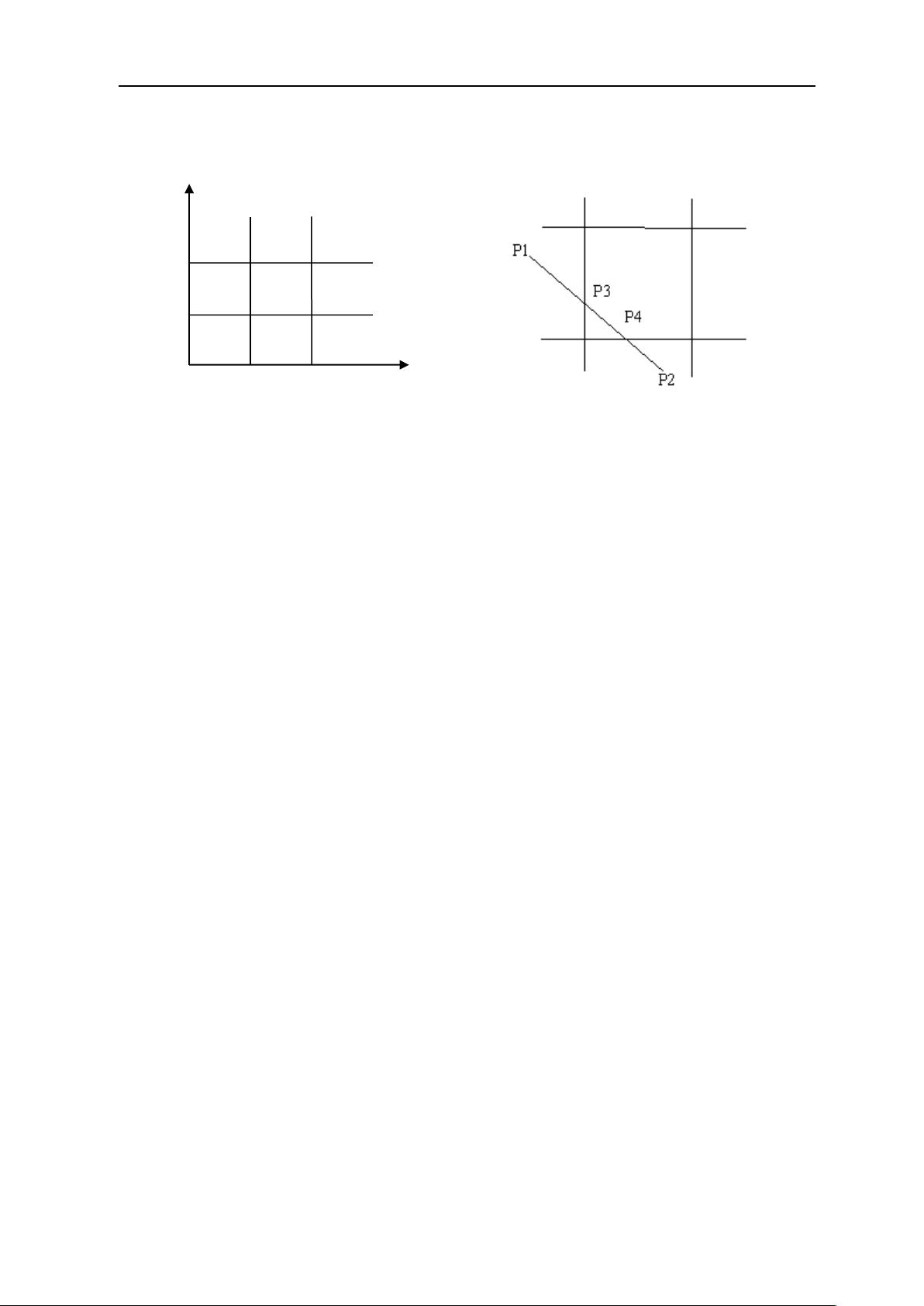
- **Sutherland-Cohen算法**:一种经典的二维图形裁剪方法,1.3.1节介绍原理和步骤,提供伪代码和流程图。
- **中点分割裁剪算法**:针对特定场景提出的一种改进方法,同样包括流程图和程序描述。
- **梁友栋-Barskey算法**:一种高效算法,1.3.3详细解释了原理和步骤。
图形求交技术则涵盖了:
- **线与线、线与面的交点求法**:这部分阐述了两种不同情况下的求解策略。
- **求交线算法**:针对线与线或线与曲线的相交情况。
- **包含判定算法**:用于判断几何对象之间的包含关系。
- **重叠判定算法**:识别两个对象是否完全或部分重叠。
- **凸包计算**:确定多边形或曲线的最小凸包围盒。
最后,论文探讨了自由曲线曲面造型技术,以Bezier曲线和曲面为例,这是计算机图形学中常见的非线性曲线表示方法,5.1节对Bezier曲线进行了详细介绍。
总体而言,这份论文深入浅出地分析了计算机图形学中的核心概念和技术,提供了实用的算法实现和比较,对于理解和应用这些技术具有较高的参考价值。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2023-06-29 上传
2023-07-09 上传
2023-06-29 上传
2023-06-29 上传
2023-06-30 上传
2023-07-04 上传
yyyyyyhhh222
- 粉丝: 461
- 资源: 6万+
最新资源
- Elasticsearch核心改进:实现Translog与索引线程分离
- 分享个人Vim与Git配置文件管理经验
- 文本动画新体验:textillate插件功能介绍
- Python图像处理库Pillow 2.5.2版本发布
- DeepClassifier:简化文本分类任务的深度学习库
- Java领域恩舒技术深度解析
- 渲染jquery-mentions的markdown-it-jquery-mention插件
- CompbuildREDUX:探索Minecraft的现实主义纹理包
- Nest框架的入门教程与部署指南
- Slack黑暗主题脚本教程:简易安装指南
- JavaScript开发进阶:探索develop-it-master项目
- SafeStbImageSharp:提升安全性与代码重构的图像处理库
- Python图像处理库Pillow 2.5.0版本发布
- mytest仓库功能测试与HTML实践
- MATLAB与Python对比分析——cw-09-jareod源代码探究
- KeyGenerator工具:自动化部署节点密钥生成