AWG技术在非阻塞Clos网络中的应用与挑战

5 浏览量更新于2024-08-27 收藏 3.28MB PDF 举报

"基于AWG的非阻塞Clos网络" 这篇研究论文深入探讨了基于Arrayed Waveguide Gratings (AWG)的非阻塞Clos网络设计。Clos网络是一种多级交换架构，至今仍被广泛应用于实际的交换系统中。它的主要优势在于其模块化结构，能够适应技术的不断变革。 AWG是光通信中的关键器件，具有波长路由特性，允许在不同的光纤路径之间复用和解复用不同波长的光信号。在构建非阻塞和无冲突的波分复用（WDM）交换网络时，一个重要的挑战是确保同一波长上的两个呼叫能够通过独立的链路连接，或者通过可调谐波长转换器（TWC）将它们转换到不同的波长上，以避免信号干扰。论文作者Tong Ye、Tony T. Lee和Weisheng Hu提出了一种逻辑方案，将WDM交换网络划分为多个波长自主的单元或“细胞”。这种分区策略有助于解决波长可扩展性问题，即在保持非阻塞特性的前提下，减少对TWC的转换范围需求。通过这种方式，可以有效地降低对波长粒度的依赖，同时减小TWC的复杂性和成本。此外，论文还可能讨论了如何优化AWG的使用以提高网络效率，包括如何安排波长分配，以及如何通过控制AWG的复用和解复用功能来实现灵活的路径选择。可能还涉及了如何处理波长冲突，以及在网络中引入光缓存或光交叉连接技术以进一步提升性能。这篇论文为理解和设计高效、可扩展的基于AWG的非阻塞Clos网络提供了理论基础和技术指导，对于推动光通信领域的研究和发展具有重要意义。它不仅关注了网络的物理层特性，还涉及了网络层次的算法和控制策略，展示了如何通过创新设计克服技术限制，实现高性能的光交换。

YE et al.: AWG-BASED NON-BLOCKING CLOS NETWORKS 493

Fig. 2. Call in a WDM switch.

NB2) modularize AWGs;

NB3) scale down the conversion range of TWCs;

NB4) and reuse the same wavelength set in the recursive

construction of the network to reduce the wavelength

granularity.

The objective NB1 is consistent with the RNB condition of the

traditional Clos networks, while

are additional

requirements for WDM-based Clos networks.

The rest of this paper is organized as follows. In Section II,

we brieﬂy introduce the function of the AWGs and TWCs and

show how a WDM switching network can be constructed from

the combination of AWGs and TWCs. In Section III, we con-

struct a three-stage AWG-based Clos network, based on the

non-blocking and contention-free principle of WDM switches.

We present the routing algorithm of this network and show that

the network is fully utilized if all input and output wavelength

channels are busy. Section IV proposes a recursive construction

scheme to achieve the scalability of AWG-based Clos networks.

We show that this scheme scales down the AWGs and substan-

tially reduces wavelength granularity of the network and, thus,

the conversion range of the TWCs. Section V concludes this

paper with a comparison of our results to previous results.

II. P

RELIMINARIES

In this paper, we study the wavelength-based

communication

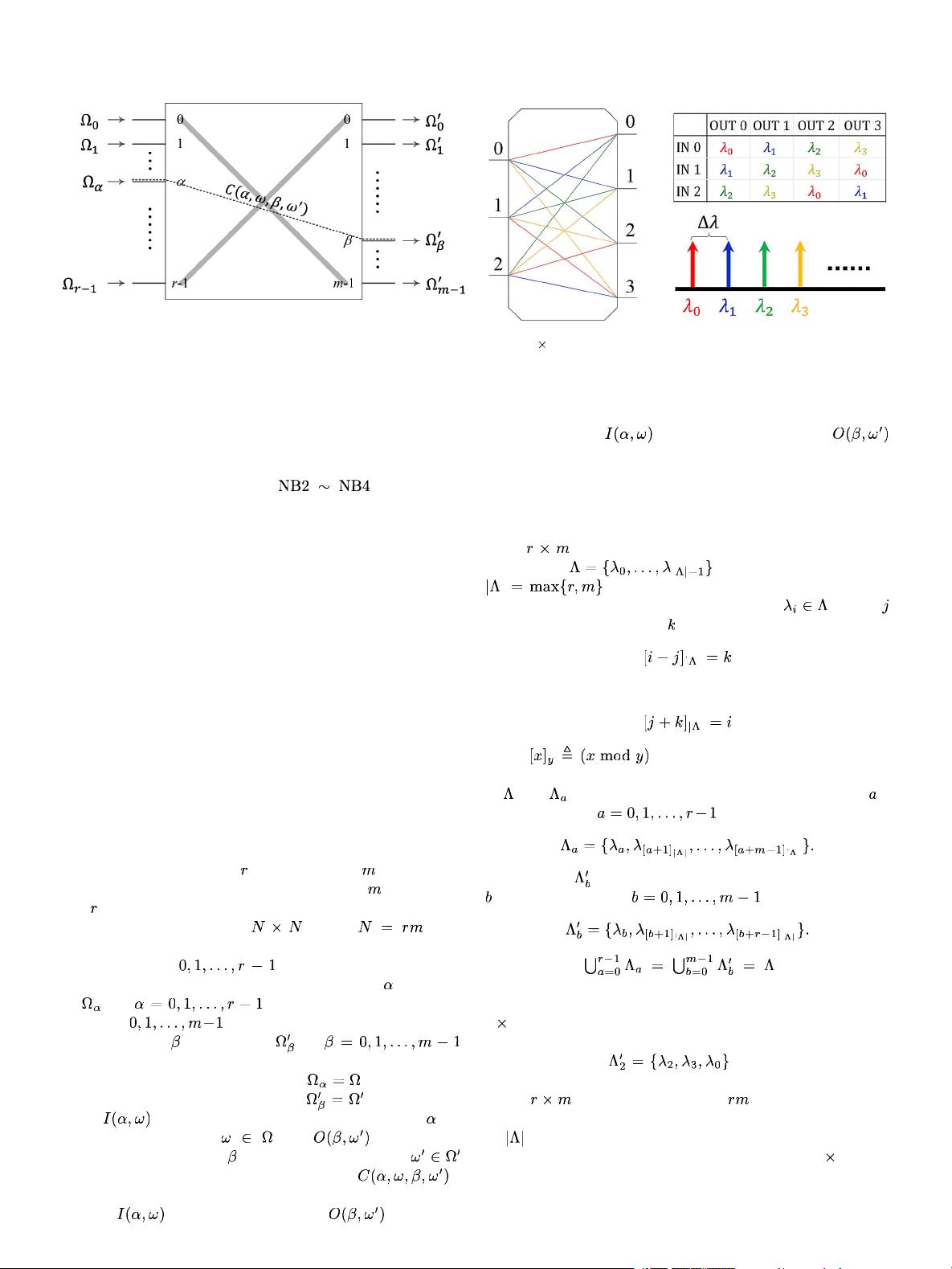
model [9]. The WDM switch under consideration is illustrated

in Fig. 2. This switch has

input ports and output ports,

and each input port and each output port ca

rries

wavelengths

and

wavelengths, respectively. Thus, the dimension of this

WDM switching network is ,where is the

number of input (output) wavelength

channels. The input ports

are numbered by

from the top to the bottom.

The set of wavelengths carried by the input port

is denoted

,for . Similarl

y, the output ports are

labeled by , and the set of wavelengths associated

with output port is denoted as for .

Furthermore, without loss

of generality, we assume that input

wavelength sets are all the same, (i.e.,

), and the output

wavelength sets are all the same (i.e., ).

Let

denote the

input channel at the input port

car-

ried by the wavelength

,and be the output

channel at the output port carried by the wavelength .

As illustrated by

the dotted line in Fig. 2, a call

the WDM switch is deﬁned as a connection between the input

channel

and the output channel . This paper

Fig. 3. 3 4 AWG and its routing table.

focuses on the AWG-based WDM switches with RNB proper-

ties, meaning that a call can always be established between an

idle input channel

and an idle output channel

with possible rearrangements of existing connections. To facili-

tate our discussion, we ﬁrst describe the functions of AWG and

TWC in a WDM switch.

A. AWG

AWG is associated with a set of equally spaced

wavelengths

in its principal FSR, where

. The AWG has a cyclic wavelength routing

property: The signal carried by the wavelength at input

will be forwarded to output if

(1)

or equivalently

(2)

where

. From (2), it is easy to see that each

input port of the AWG is associated with a wavelength subset

.Let be the wavelength subset associated with the th

input port, where . According to (2), we have

Similarly, let be the wavelength subset associated with the

th output port, where .Wehave

It is clear that .Wehaveshown

in [2] that such wavelength assignment of the AWGs is con-

tention-free. As an example, t

he wavelength assignments of the

4 AWG shown in Fig. 3 are tabulated in a contention-free

routing table, in which the output port 2 is associated with the

wavelength subset

. For a symmetric AWG,

the routing table is a Latin square.

The

AWG provides a set of ﬁxed interconnection

channels between its i

nput ports and output ports via a group

wavelengths [2]. For example, the 12 interconnection

channels between the inputs and the outputs of a 3 4AWG

areshowninFig.3

. Larger AWGs can provide much richer

interconnection channels. However, the results in [6] show

that the AWG with a large port count suffers serious coherent

剩余13页未读，继续阅读

weixin_38587473

粉丝: 7
资源: 891

AWG技术在非阻塞Clos网络中的应用与挑战

基于SOA和AWG的非相干可重构微波光子滤波器实验研究

全光WDM组播与单播方案：基于SOA和AWG的光接入网技术

基于DDS的单片机-CPLD超声波信号源AWG设计与应用

AWG技术在非阻塞Clos网络中的应用与挑战

基于AWG的同步多通道锁模激光器

24AWG/28AWG网络跳线哪个好？使用28AWG网络跳线的好处

基于AWG的单片4 x 12 GHz多通道谐波锁模激光器

单片集成的基于AWG的多通道谐波锁模激光器的同步操作

用于多通道同步超短脉冲生成的低成本基于AWG的基频锁模半导体激光器

紧凑且可调谐的基于AWG的实时延迟，适用于多Gbps无线电波束成形器

最新资源