MeanShift算法详解：历史、发展与应用

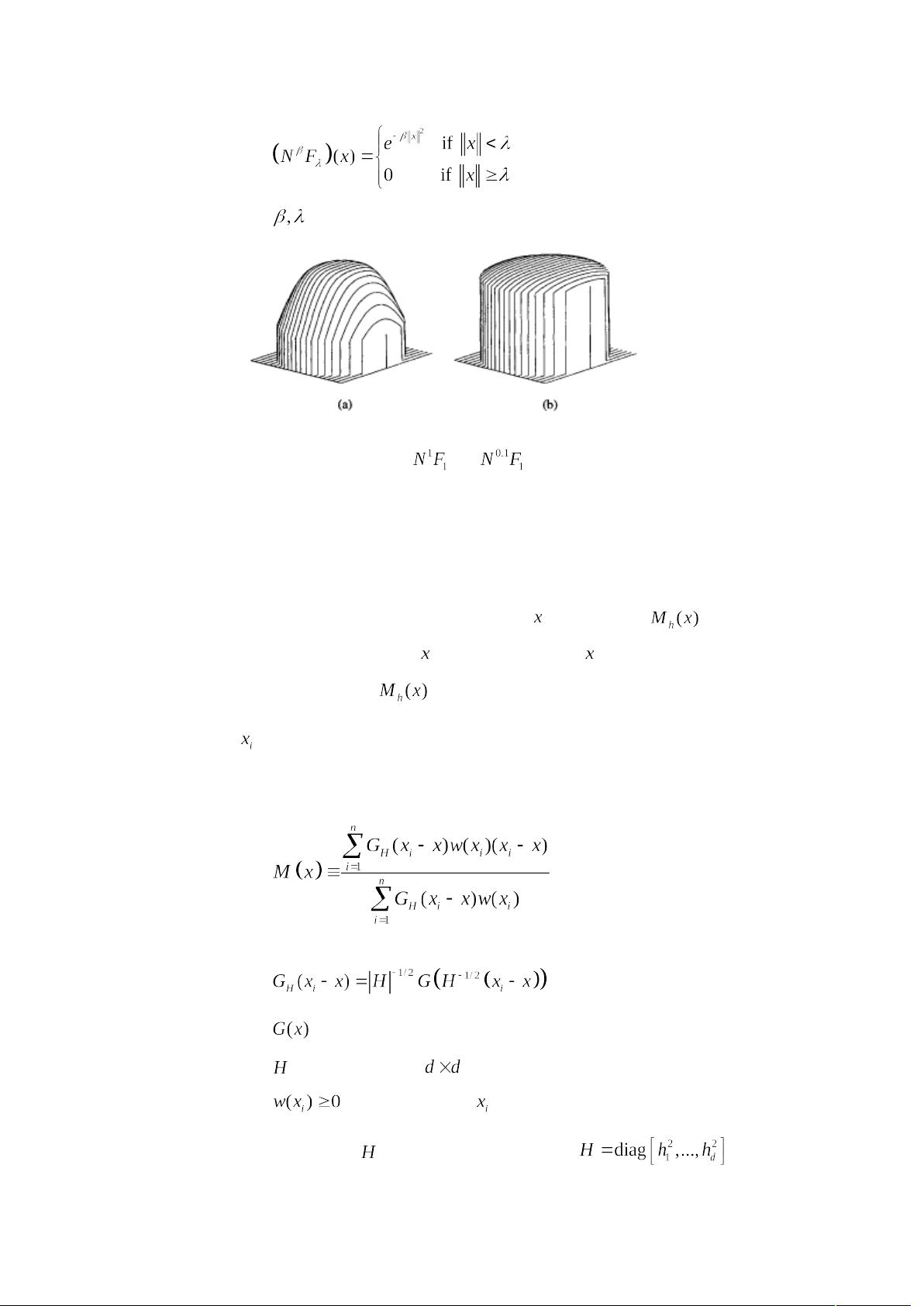
MeanShift是一种无参数的非监督聚类算法，最初由Fukunaga等人在1975年的论文中提出，作为概率密度梯度函数估计的一种方法。算法的核心思想是基于数据点周围的密度分布来移动，直至找到局部密度最大区域，从而形成聚类。最初的MeanShift仅是一个迭代过程，即计算每个点的偏移均值并移动至该点，重复此过程直到满足停止条件。 然而，MeanShift真正受到广泛关注是在1995年Yizong Cheng发表的一篇文章中。Cheng对MeanShift做了重要扩展：他引入了一族核函数，允许根据样本点与中心点距离的不同调整偏移量，赋予不同样本不同的权重，这增加了算法的灵活性和适用性。他还明确了MeanShift在概率密度函数估计和模态检测中的应用潜力，并展示了其在诸如图像平滑、图像分割和非刚体对象跟踪等领域的实际应用。 Comaniciu等人进一步发展了MeanShift，将其应用于特征空间分析，通过计算每个像素点的MeanShift向量来实现图像平滑和区域分割。他们证明，在一定条件下，MeanShift会收敛到概率密度函数的最大值，即模态，从而成为一种有效的聚类工具。 MeanShift的基本步骤包括： 1. 初始化：选择任意一点作为起始点。 2. 移动：计算当前点周围密度高的邻域，找到该区域的质心（MeanShift向量）。 3. 更新：将点移动到新的质心位置。 4. 重复：直到达到停止条件，如达到预设迭代次数或相邻两次移动的距离小于阈值。 在实际应用中，MeanShift展示了强大的性能，尤其是在处理高维数据、非凸形状的聚类和实时跟踪任务时。它的优点在于无需预先设定簇的数量或形状，能够自动发现数据集中的自然结构。然而，MeanShift的缺点包括对初始点选择敏感、计算复杂度相对较高以及对于噪声和异常值较为敏感。 MeanShift聚类算法是一个基于密度的动态搜索过程，通过不断移动样本点直到达到局部密度极大点，实现数据的自我组织和聚类。随着理论和应用的发展，MeanShift已经成为数据挖掘和计算机视觉领域不可或缺的工具。