粘性流体边界层：Falkner-Skan方程的Adomian解法

"这篇论文研究了粘性流体绕流楔型物体时Falkner-Skan边界层方程的求解方法。通过Adomian拆分技术和Crocco变量变换，将无穷区间的边界值问题转化为初值问题，并利用Padé逼近来确定初始条件，从而得到了一种有效的近似解析解。此外，论文还设计了一种数值解法，并对比了该近似解析解与Hartree等早期研究者的成果，验证了解法的准确性和可靠性。" Falkner-Skan方程是描述粘性流体绕过楔型物体时边界层流动的典型方程，最初由V. M. Falkner和S. W. Skan于1931年提出。这个方程在流体力学中具有重要地位，因为它涉及到层流边界层的相似解。方程的形式为f' + ff'' + β(1 - f'^2) = 0，其中f是独立变量的函数，'和''分别代表一阶和二阶导数，β是压力梯度，表示流体的压力变化情况。当β>0时，表示顺压梯度；β=0表示无压力梯度；β<0则表示逆压梯度。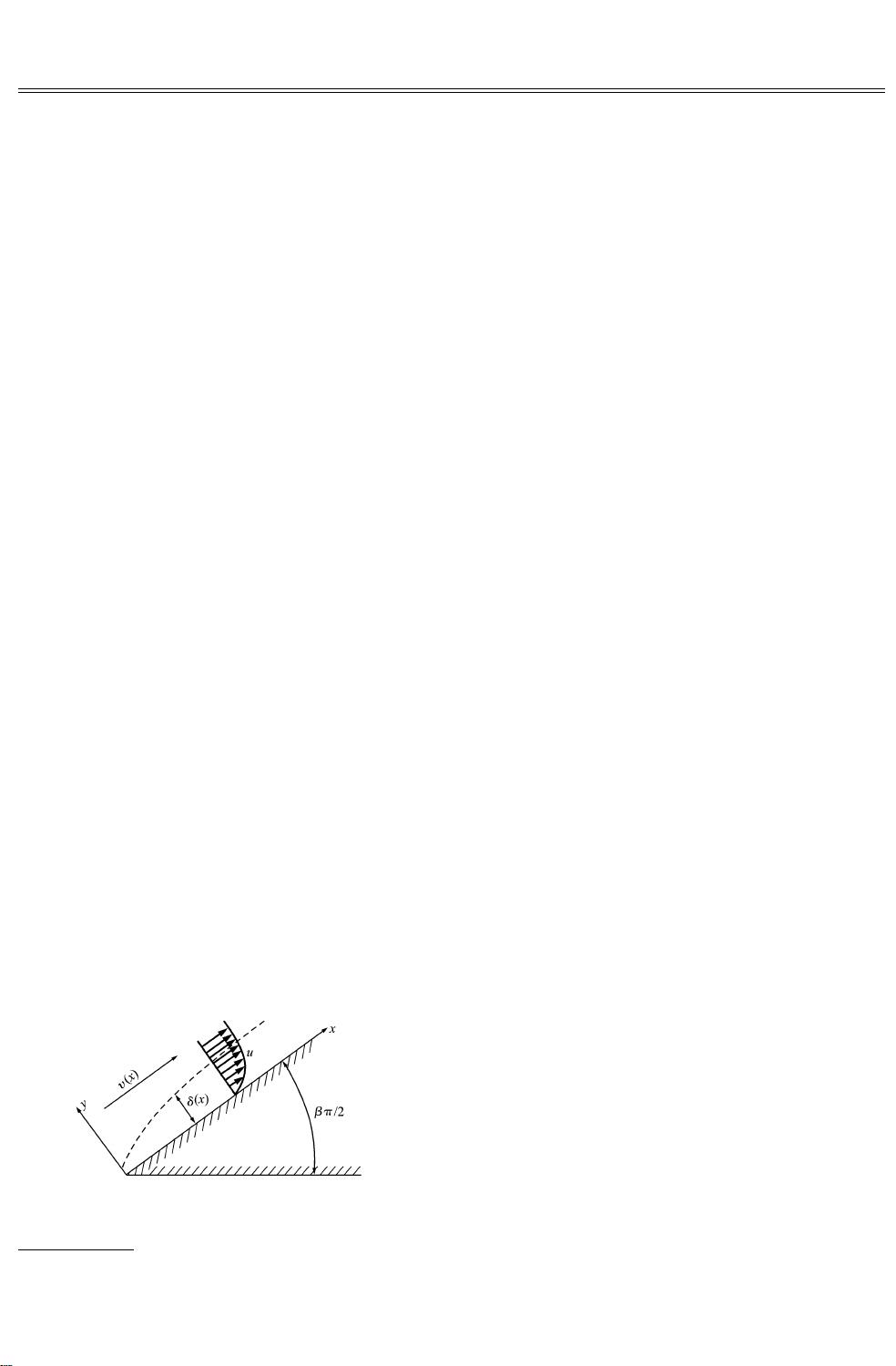 边界条件为f(0)=f'(0)=0，表示在楔型物体表面边界层的厚度和速度梯度为零，而f'(∞)=1则表示边界层在远离物体的位置趋向自由流的速度。对于楔形半顶夹角为πβ/2（0<β≤2）的情况，流体的流动在前驻点附近具有相似性，这使得Falkner-Skan方程成为研究此类问题的重要工具。 论文采用Adomian拆分方法，这是一种非线性微分方程的数值分析技术，可以将复杂的非线性问题分解为一系列简单的部分，便于求解。同时，通过引入Crocco变量变换，可以将原问题从无穷区间转化为有限区间的初值问题。Padé逼近是数值分析中的一个技巧，用于逼近函数，它在这里被用来确定解的初始条件，从而获得更精确的近似解析解。 为了进一步验证这种方法的有效性，论文还设计了一种数值解法，并将得到的近似解析解与Hartree等早期研究者的结果进行对比。这种比较有助于确认新方法的准确性和可靠性，为理解和模拟粘性流体绕流楔型物体的边界层流动提供了新的工具和理论支持。 这篇2008年的研究工作为Falkner-Skan方程的求解提供了一个新的视角，不仅提出了一种近似解析解的计算策略，还通过数值方法证明了解的正确性，对流体力学领域的研究具有重要价值。