计算机网络第四版：课后习题与解答解析

5星 · 超过95%的资源需积分: 32 186 浏览量更新于2024-07-29 收藏 917KB PDF 举报

"该资源是计算机网络（第四版）的课后习题集与解答，由Andrews和Tanenbaum编写，包含了易、中、难三个等级的问题以及删除部分。习题涵盖从基础概念到深入技术的各个方面，旨在帮助学习者巩固和深化对计算机网络的理解。" 计算机网络是信息技术领域中的核心学科，主要研究计算机之间的通信、数据传输和资源共享。本资源提供的习题集和答案可以帮助学习者系统地掌握计算机网络的基本原理和技术。 1. **客户端-服务器系统的优点** (M级，中等难度) - **扩展性**：客户端-服务器(C/S)系统允许轻松添加更多节点，使得网络能够适应用户数量的增长。 - **容错性**：通过镜像服务器等机制，即使单个组件失效，系统仍能继续运行，提高了系统的可用性和可靠性。 - **计算能力**：局域网(LAN)提供了更强的计算能力，因为多个客户端可以共享服务器的处理能力。 - **交互性**：LAN模型提供了更好的交互式用户体验，因为服务器可以快速响应客户端请求。 2. **网络性能因素** (E级，简单) - **带宽**：衡量网络每秒能传输多少比特，是决定数据传输速率的关键因素。 - **延迟**：指第一个比特从客户端传送到服务器所需的时间，影响了用户的响应感知。 - 高带宽高延迟的例子：跨大陆的光纤连接，虽然传输速度快，但由于距离长，信号传播延迟大。 - 低带宽低延迟的例子：同一座大楼内用56kbps调制解调器进行的连接，虽然传输速率低，但因距离短，延迟较小。 3. **评估网络质量的其他参数** (E级，简单) - **丢包率**：网络在传输过程中丢失数据包的比例，高丢包率可能导致数据丢失或重传，影响服务质量。 - **抖动**：数据包到达时间的不一致性，对于实时应用如音频和视频流很重要。 - **可靠性**：网络连接的稳定性和持久性，反映网络故障发生的频率。 - **吞吐量**：实际传输数据的速度，可能受到带宽、拥塞控制等因素的影响。 - **并发性**：网络同时处理多个连接的能力，对于多用户环境至关重要。 4. **网络层次结构** (M级，中等) - 计算机网络通常采用OSI七层模型或TCP/IP四层模型，每层负责特定的功能，如物理层处理信号传输，应用层处理用户接口。 5. **协议的重要性** (H级，困难) - 网络中的通信依赖于各种协议，如TCP/IP协议族中的TCP用于可靠传输，IP用于寻址和路由，HTTP用于网页传输等。通过解决这些习题，学习者可以深入理解计算机网络中的关键概念，如网络架构、性能指标、通信协议以及问题排查。同时，习题答案提供了清晰的解释，有助于自我检查和理解。

第 1 列，流 2 的第 1 列，流 3 的第 1 列，随后是流 1 的第 2 列，流 2 的第 2 列，

以此类推，最后形成 270 列宽 9 行高的帧。

OC-3c 流中的用户实际数据传输速率比 OC-3 流的速率略高（149.760Mbps 和

148.608Mbps），因为路径开销仅在 SPE 中出现一次，而不是当使用 3 条单独 OC-1

流时出现的 3 次。换句话说，OC-3c 中 270 列中的 260 列可用于用户数据，而在

OC-3 中仅能使用 258 列。更高层次的串联帧（如 OC-12c）也存在这样的情况。]]

OC-12c 帧有 12*90=1080 列和 9 行。其中段开销和线路开销占 12*3=36 列，这

样同步载荷信封就有 1080-36=1044 列。SPE 中仅 1 列用于路径开销，结果就是 1043

列用于用户数据。

由于每列 9 个字节，因此一个 OC-12c 帧中用户数据比特数是 8 ×9×1043＝75096。

每秒 8000 帧，得到用户数据速率 75096×8000 =600768000bps，即 600.768Mbps。

所以，在一条 OC-12c 连接中可提供的用户带宽是 600.768Mbps。

41. Three packet-switching networks each contain n nodes. The first network has

a star topology with a central switch, the second is a (bidirectional) ring, and the

third is fully interconnected, with a wire from every node to every other node. What

are the best-, average-, and-worst case transmission paths in hops?（E）

三种网络的特性如下：

星型：最好为2，最差为 2，平均为 2；

环型：最好为 1，最差为 n/2，平均为 n/4

如果考虑 n 为奇偶数，

则 n 为奇数时，最坏为（n-1）/2，平均为（n+1）/4

n 为偶数时，最坏为 n/2，平均为 n

/4(n1) 

全连接：最好为 1，最差为 1，平均为 1。

42. Compare the delay in sending an x-bit message over a k-hop path in a

circuit-switched network and in a (lightly loaded) packet-switched network. The

circuit setup time is s sec, the propagation delay is d sec per hop, the packet size is p

bits, and the data rate is b bps. Under what conditions does the packet network have

a lower delay?(M)

对于电路交换， t= s 时电路建立起来；t＝s+x/d 时报文的最后一位发送完毕；t=

s+x/d+kb 时报文到达目的地。而对于分组交换，最后一位在 t=x/b时发送完毕。

为到达最终目的地，最后一个分组必须被中间的路由器重发 k-1 次，每次重发花

时间 p/b，所以总的延迟为

为了使分组交换比电路交换快，必须：

所以：

43. Suppose that x bits of user data are to be transmitted over a k-hop path in a

packet-switched network as a series of packets, each containing p data bits and h

header bits, with x >>p + h. The bit rate of the lines is b bps and the propagation

delay is negligible. What value of p minimizes the total delay?（M）

所需要的分组总数是 x/p，因此加上头信息的总数据量为(p+h)x/p 位。

源端发送这些位需要时间为(p+h)x/pb，

中间的路由器重传最后一个分组所花的总时间为(k-1)(p+h)/b，

因此我们得到的总的延迟为，

对该函数求 p 的导数，得到，令得到

因为p＞0，所以故时能使总的延迟最小。

44. In a typical mobile phone system with hexagonal cells, it is forbidden to reuse

a frequency band in an adjacent cell. If 840 frequencies are available, how many can

be used in a given cell?（B）

每个蜂窝单元都有 6 个邻居。假定中间的单元使用频率 A，它的邻居则可以依次

使用 B，C，B，C，B，C，也就是说，只需用三个相互独立的单元就足够了。所以，

每个单元可以使用 280 种频率。

47. Sometimes when a mobile user crosses the boundary from one cell to another,

the current call is abruptly terminated, even though all transmitters and receivers

are functioning perfectly. Why?（E）

在邻近的蜂窝单元中频率不能复用。所以当一名用户从一个单元移动到另一个单

元时，必须给他分配一个新的频率。如果当用户移到一个新的单元，但是当前的新

单元中的所有频率都在使用中，则用户的呼叫必须被终止。

48. D-AMPS has appreciably worse speech quality than GSM. Is this due to the

requirement that D-AMPS be backward compatible with AMPS, whereas GSM had

no such constraint? If not, what is the cause?（M）

It is not caused directly by the need for backward compatibility. The 30 kHz channel

was indeed a requirement, but the designers of D-AMPS did not have to stuff three users

into it. They could have put two users in each channel, increasing the payload before

error correction from 260 ×50=13 kbps to 260×75 =19.5 kbps. Thus, the quality loss was

an intentional trade-off to put more users per cell and thus get away with bigger cells.

49. Calculate the maximum number of users that D-AMPS can support

simultaneously within a single cell. Do the same calculation for GSM. Explain the

difference.（M）

D-AMPS uses 832 channels (in each direction) with three users sharing a single

channel. This allows D-AMPS to support up to 2496 users simultaneously per cell. GSM

uses 124 channels with eight users sharing a single channel. This allows GSM to support

up to 992 users simultaneously. Both systems use about the same amount of spectrum (25

MHz in each direction).

D-AMPS uses 30 KHz×832 = 24.96 MHz. GSM uses 200 KHz ×124 =24.80 MHz.

The difference can be mainly attributed to the better speech quality provided by GSM (13

Kbps per user) over D-AMPS (8 Kbps per user).

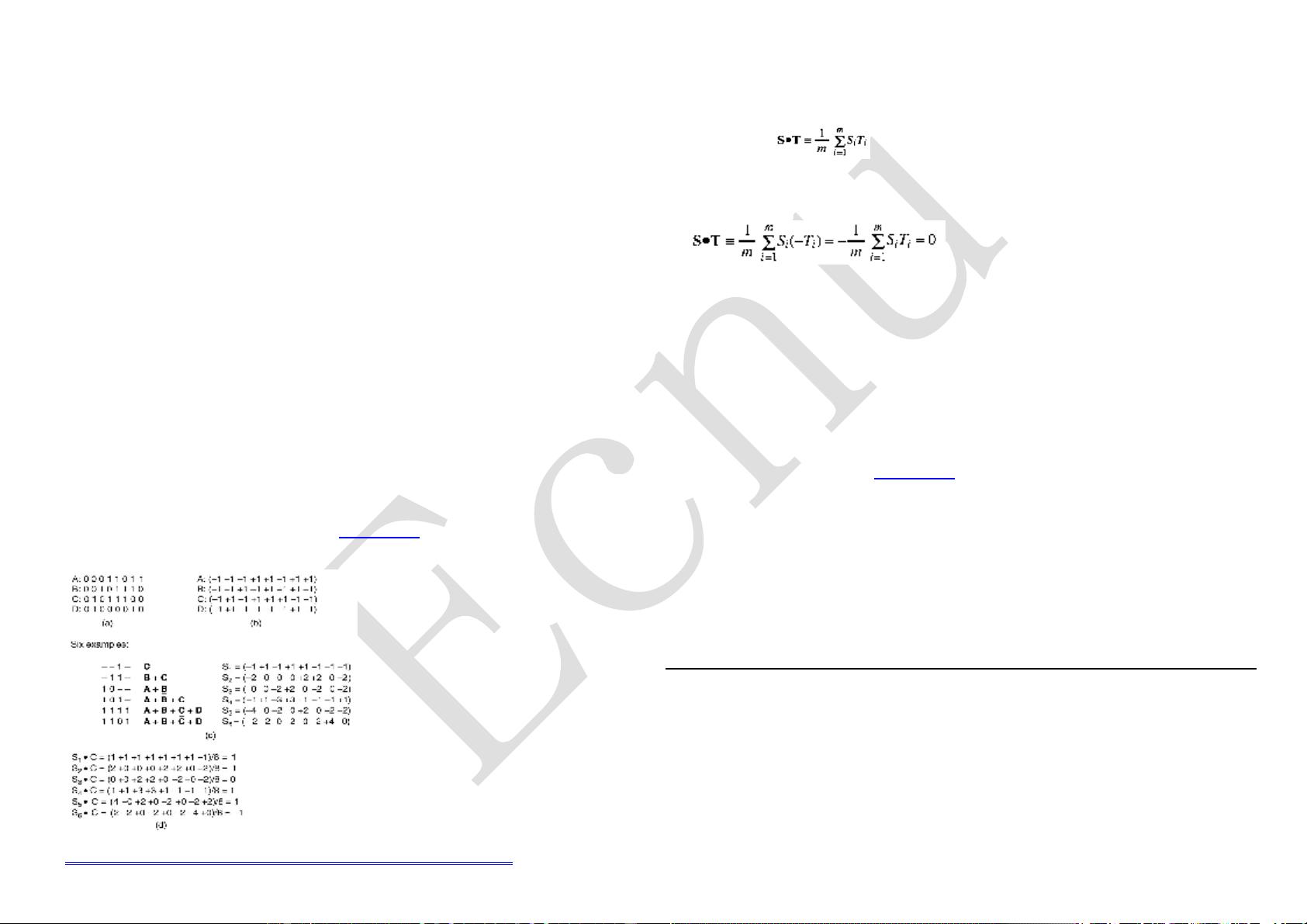
50. Suppose that A, B, and C are simultaneously transmitting 0 bits, using a

CDMA system with the chip sequences of Fig. 2-45(b). What is the resulting chip

sequence?（E）

传输 0，则时间片序列取其补码，传输 1，则时间序列取其本身。

将 A，B，C 相加后，取补码得结果为：(+3 +1 +1 -1 -3 -1 -1 +1).

51. In the discussion about orthogonality of CDMA chip sequences, it was stated

that if S•T = 0 then S•T is also 0. Prove this.(E)

By definition

If T sends a 0 bit instead of 1 bit, its chip sequence is negated, with the i-th element

becoming Ti . Thus,

52. Consider a different way of looking at the orthogonality property of CDMA

chip sequences. Each bit in a pair of sequences can match or not match. Express the

orthogonality property in terms of matches and mismatches.

When two elements match, their product is +1. When they do not match, their product

is -1. To make the sum 0, there must be as many matches as mismatches. Thus, two chip

sequences are orthogonal if exactly half of the corresponding elements match and exactly

half do not match.

53. A CDMA receiver gets the following chips: (-1 +1 -3 +1 -1 -3 +1 +1). Assuming

the chip sequences defined in Fig. 2-45(b), which stations transmitted, and which

bits did each one send?（E）

分别与（-1 +1 -3 +1 -1 -3 +1 +1）做内积：

A：（-1 +1 -3 +1 -1 -3 +1 +1）d (-1 -1 -1 +1 +1 -1 +1 +1) /8 = 1

B：（-1 +1 -3 +1 -1 -3 +1 +1）d (-1 -1 +1 -1 +1 +1 +1 -1) /8 = -1

C：（-1 +1 -3 +1 -1 -3 +1 +1）d (-1 +1 -1 +1 +1 +1 -1 -1) /8 = 0

D：（-1 +1 -3 +1 -1 -3 +1 +1）d (-1 +1 -1 -1 -1 -1 +1 -1) /8 = 1

所以 A，D 发送的都是 1 bits，B 发送的是 0 bit,，C 没有发送

Chapter 3 The Data Link Layer Problems

1. An upper-layer packet is split into 10 frames, each of which has an 80 percent

chance of arriving undamaged. If no error control is done by the data link protocol,

how many times must the message be sent on average to get the entire thing through?

（E）

由于每一帧有 0.8 的概率正确到达，整个信息正确到达的概率为 p=0.8

=0.107。

为使信息完整的到达接收方，发送一次成功的概率是 p ，二次成功的概率是

(1-p)p，三次成功的概率为(1-p)

p，i 次成功的概率为(1-p)

i-1 

p，因此平均的发送次

剩余35页未读，继续阅读

孤单一吻

粉丝: 8
资源: 9

计算机网络第四版：课后习题与解答解析

计算机网络(第四版)课后习题(英文)+习题答案(中英文).pdf

计算机网络(第四版)课后习题(英文)+习题答案(中英文

计算机网络（英文第四版）课后习题答案

计算机网络第六英文版教材+中文版教材+课后习题答案+实验代码+wireshark使用教程

计算机网络(第五版)课后习题(英文)+习题答案(中英文)

计算机网络第四版课后习题答案

华工计算机网络（第四版）课后习题（英文）习题答案（中英文）

计算机网络教程第四版课后习题答案

韩家炜数据挖掘概念与技术（第二版）中英文+课后习题答案中英文合集

计算机网络第六版课后习题答案

最新资源