SWAN指南：输入设置与变量输出详解

需积分: 49 101 浏览量更新于2024-07-18 2 收藏 420KB PDF 举报

Swan是一款专业的海洋波浪数值模拟软件，专为理解和预测海洋波浪行为而设计。此用户手册针对的是SWAN Cycle III版本40.51，由荷兰代尔夫特理工大学环境流体动力学系的SWAN团队开发。手册的版权允许用户在遵循GNU自由文档许可证（v1.2或更高版本）的前提下复制、分发和修改文档。 1. **简介**：Swan提供了全面的海洋波浪模型，用于研究风浪生成、传播、衰减以及对海岸线的影响。它特别适用于海洋工程、气象预报和气候变化研究等领域。 2. **通用定义与注意事项** - **介绍**：手册首先解释了Swan的基本概念，包括其在波浪模拟中的作用和目标。 - **局限性**：讨论了Swan可能存在的限制，如特定场景下的适用性、假设条件或已知的不足之处。 - **内部机制与问题**：涵盖了软件的工作原理、内置场景处理、极限值设置以及潜在的编程错误和缺陷。 3. **与其他模型的关系**：手册还提到了Swan与WAM（Wave Action Model）、WAVEWATCH III等其他波浪模型的比较，有助于用户理解Swan的独特优势和与其他工具的差异。 4. **单位与坐标系统**：Swan支持多种单位和坐标系统，这对于国际交流和应用多样性至关重要，用户需要了解如何正确设置这些参数以适应不同的研究需求。 5. **网格选择、时间窗口及边界条件**：这是关键部分，讲解了如何设置模拟区域的网格结构（空间分辨率、边界条件），选择合适的时间窗口（步长、时段长度），以及设定初始和猜测条件，这些都是影响模拟结果精度的重要因素。 6. **输入文件设置**：手册详细解释了如何准备和配置input文件，这是启动模拟的起点，文件中包含了所有必要的物理参数、边界条件和模型设置。 7. **输出变量**：最后，手册介绍了Swan能够生成的各种输出变量，包括但不限于波浪高度、频率、方向、能量分布等，以便用户分析和解读模拟结果。通过阅读Swan用户手册，用户可以更好地掌握这款软件的使用方法，优化模拟过程，并确保得出可靠和准确的海洋波浪动态分析。对于任何从事海洋科学计算或工程应用的人来说，理解和熟练操作Swan是至关重要的。

8 Chapter 2

locations of the various grids are determined with respect to the problem coordinates. All

grid points of a curvi-linear grid are relative to the problem coordinate system.

2.6 Choice of grids, time windows and boundary /

initial / ﬁrst guess conditions

2.6.1 Introduction

Several types of grids and time window(s) need to be deﬁned: (a) spectral grid, (b) spatial

(geographic) grids and time window(s) in case of non-stationary computations.

The spectral grid that need to be deﬁned by the user is a computational

spectral grid on

which SWAN performs the computations.

SWAN has the option to make computations that can be nested in (coarse) SWAN, WAM

or WAVEWATCH III. In such cases, the spectral grid need not be equal to the spectral

grid in the coarse SWAN, WAM or WAVEWATCH III run.

The spatial grids that need to be deﬁned by the user are (if required):

• a computational spatial grid on which SWAN performs the computations,

• one (or more) spatial input grid(s) for the bottom, current ﬁeld, water level, bottom

friction and wind (each input grid may diﬀer from the others) and

• one (or more) spatial output grid(s) on which the user requires output of SWAN.

The wind and bottom friction do not require a grid if they are uniform over the area of

interest.

For one-dimensional situations, i.e. ∂/∂y ≡ 0, SWAN can be run in 1D mode.

If a uniform, rectangular computational spatial grid is chosen in SWAN, then all input and

output grids must be uniform and rectangular too, but they may all be diﬀerent from each

other.

If a curvi-linear computational spatial grid is chosen in SWAN, then each input grid should

be either uniform, rectangular or identical to the used curvi-linear grid or staggered with

respect to the curvi-linear computational grid.

SWAN has the option to make computations that are nested in (coarse) SWAN, WAM or

WAVEWATCH III. In such runs, SWAN interpolates the spatial boundary of the SWAN,

WAM or WAVEWATCH III grid to the (user provided) grid of SWAN (that needs to

(nearly) coincide along the grid lines of WAM or WAVEWATCH III or the output nest

grid boundaries of SWAN). Since, the computational grids of WAM and WAVEWATCH

General deﬁnitions and remarks 9

III are in spherical coordinates, it is recommended to use spherical coordinates in a nested

SWAN when nesting in WAM or WAVEWATCH III.

Nesting from a 2D model to a 1D model is possible although is should not be done by

using the commands NGRID and NEST. Instead, deﬁne the boundary point of the 1D model

as an output point (using command POINTS) and write the spectra for that point using

the command SPECout. In the 1D model, this spectra is used as boundary condition using

the BOUNDSPEC command.

Similarly, the wind ﬁelds may be available in diﬀerent time windows than the current and

water level ﬁelds and the computations may need to be carried out at other times than

these input ﬁelds. For these reasons SWAN operates with diﬀerent time windows with

diﬀerent time steps (each may have a diﬀerent start and end time and time step):

• one computational time window in which SWAN performs the computations,

• one (or more) input time window(s) in which the bottom, current ﬁeld, water level,

bottom friction and wind ﬁeld (if present) are given by the user (each input window

may diﬀer form the others) and

• one (or more) output time window(s) in which the user requires output of SWAN.

SWAN has the option to make computations that are nested in SWAN, WAM or WAVE-

WATCH III. SWAN searches the boundary conditions in the relevant output ﬁle of the

previous SWAN, WAM or WAVEWATCH III runs to take the boundary conditions at the

start time of the nested run. It will not take the initial condition (i.e. over the entire com-

putational grid) for the nested run from the previous SWAN, WAM or WAVEWATCH III

run.

During the computations SWAN obtains bottom, current, water level, wind and bottom

friction information by tri-linear interpolation from the given input grid(s) and time

window(s). The output is in turn obtained in SWAN by bi-linear interpolation in space

from the computational grid; there is no interpolation in time, the output time is shifted

to the nearest computational time level. Interpolation errors can be reduced by taking the

grids and windows as much as equal to one another as possible (preferably identical). It

is recommended to choose output times such that they coincide with computational time

levels.

2.6.2 Input grid(s) and time window(s)

The bathymetry, current, water level, bottom friction and wind (if spatially variable) need

to be provided to SWAN on so-called input grids. It is best to make an input grid so large

that it completely covers the computational grid.

In the region outside the input grid SWAN assumes that the bottom level, the water level

10 Chapter 2

and bottom friction are identical to those at the nearest boundary of the input grid (lateral

shift of that boundary). In the regions not covered by this lateral shift (i.e. in the outside

quadrants of the corners of the input grid), a constant ﬁeld equal to the value at the nearest

corner point of the input grid is taken. For the current and wind velocity SWAN takes 0

m/s for points outside the input grid.

One should choose the spatial resolution for the input grids such that relevant spatial details

in the bathymetry, currents, bottom friction and wind are properly resolved. Special care

is required in cases with sharp and shallow ridges (sand bars, shoals) in the sea bottom and

extremely steep bottom slopes. Very inaccurate bathymetry can result in very inaccurate

refraction computations the results of which can propagate into areas where refraction as

such is not signiﬁcant (the results may appear to be unstable). For instance, waves skirting

an island that is poorly resolved may propagate beyond the island with entirely wrong

directions. In such a case it may even be better to deactivate the refraction computations

(if refraction is irrelevant for the problem at hand e.g. because the refracted waves will run

into the coast anyway and one is not interested in that part of the coast). In such cases the

ridges are vitally important to obtain good SWAN results (at sea the waves are ’clipped’

by depth-induced breaking over the ridges which must therefore represented in SWAN

computation). This requires not only that these ridges should be well represented on the

input grid but also after interpolation on the computational grid. This can be achieved by

choosing the grid lines of the input grid along the ridges (even if this may require some

slight ”shifting” of the ridges) and choosing the computational grid to be identical to the

input grid (otherwise the ridge may be ”lost” in the interpolation from the bottom input

grid to the computational grid).

In SWAN, the bathymetry, current, water level, wind and bottom friction may be time

varying. In that case they need to be provided to SWAN in so-called input time windows

(they need not be identical with the computational, output or other input windows). It is

best to make an input window larger than the computational time window. SWAN assumes

zero values at times before the earliest begin time of the input parameters (which may be

the begin time of any input parameter such as wind). SWAN assumes constant values

(the last values) at times after the end time of each input parameter. The input windows

should start early enough so that the initial state of SWAN has propagated through the

computational area before reliable output of SWAN is expected.

One should use a time step that is small enough that time variations in the bathymetry,

current, water level, wind and bottom friction are well resolved.

2.6.3 Computational grids and boundary / initial / ﬁrst guess

conditions

The computational spatial grid must be deﬁned by the user. The orientation (direction)

can be chosen arbitrarily.

General deﬁnitions and remarks 11

The boundaries of the computational spatial grid in SWAN are either land or water. In the

case of land there is no problem: the land does not generate waves and in SWAN it absorbs

all incoming wave energy. But in the case of a water boundary there may be a problem.

Often no wave conditions are known along such a boundary and SWAN then assumes

that no waves enter the area and that waves can leave the area freely. These assumptions

obviously contain errors which propagate into the model. These boundaries must therefore

be chosen suﬃciently far away from the area where reliable computations are needed so

that they do not aﬀect the computational results there. This is best established by varying

the location of these boundaries and inspect the eﬀect on the results. Sometimes the waves

at these boundaries can be estimated with a certain degree of reliability. This is the case if

(a) results of another model run are available (nested computations) or, (b) observations

are available. If model results are available along the boundaries of the computational

spatial grid, they are usually from a coarser resolution than the computational spatial grid

under consideration. This implies that this coarseness of the boundary propagates into

the computational grid. The problem is therefore essentially the same as if no waves are

assumed along the boundary except that now the error may be more acceptable (or the

boundaries are permitted to be closer to the area of interest). If observations are available,

they can be used as input at the boundaries. However, this usually covers only part of the

boundaries so that the rest of the boundaries suﬀer from the same error as above.

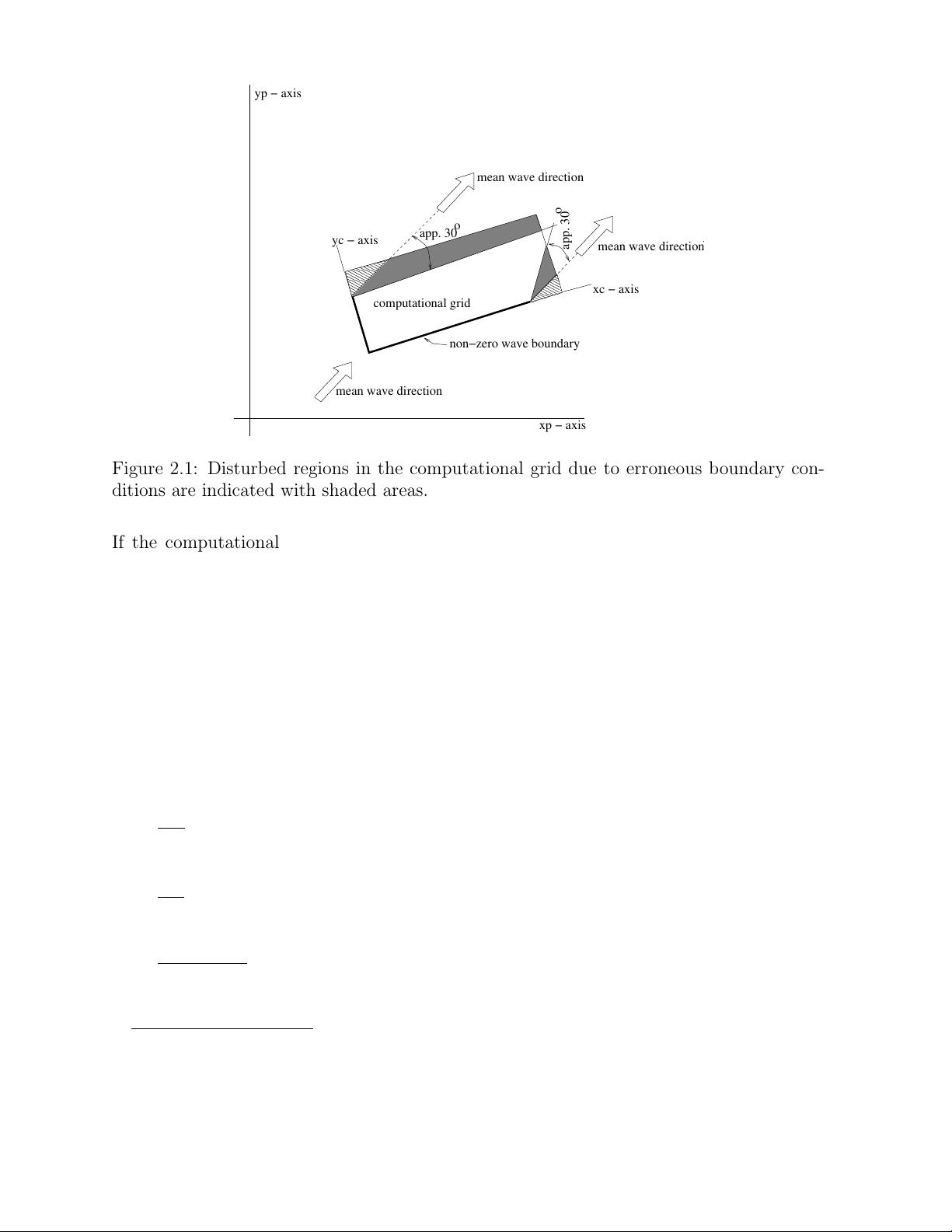
A special case occurs near the coast. Here it is often possible to identify an up-wave

boundary (with proper wave information) and two lateral boundaries (with no or partial

wave information). The aﬀected areas with errors are typically regions with the apex

at the corners of the water boundary with wave information, spreading towards shore at

an angle of 30

to 45

for wind sea conditions to either side of the imposed mean wave

direction (less for swell conditions; the angle is essentially the one-sided width of the

directional distribution of wave energy). For propagation of short crested waves (wind sea

condtions) an example is given in Figure 2.1. For this reason the lateral boundaries should

be suﬃciently far away from the area of interest to avoid the propagation of this error

into this area. Such problems do not occur if the lateral boundaries contain proper wave

information over their entire length e.g. obtained from a previous SWAN computation or

if the lateral boundaries are coast.

When output is requested along a boundary of the computational grid, it may occur that

this output diﬀers from the boundary conditions that are imposed by the user. The reason

is that SWAN accepts only the user-imposed incoming wave components and that it re-

places the user-imposed outgoing wave components with computed outgoing components

(propagating to the boundary from the interior region). Moreover, SWAN has an option to

only compute within a pre-set directional sector (pre-set by the user). Wave components

outside this sector are totally ignored by SWAN (no replacements either). The user is

informed by means of a WARNING in the output when the computed signiﬁcant wave

height diﬀers more than 10%, say (10% is default), from the user-imposed signiﬁcant wave

height (command BOUND...). The actual value of this diﬀerence can be set by the user (see

the SET command).

12 Chapter 2









computational grid

non−zero wave boundary

xp − axis

yp − axis

mean wave direction

yc − axis

xc − axis

app. 30

Figure 2.1: Disturbed regions in the computational grid due to erroneous boundary con-

ditions are indicated with shaded areas.

If the computational grid extends outside the input grid, the reader is referred to Sec-

tion 2.6 to ﬁnd the assumptions of SWAN on depth, current, water level, wind, bottom

friction in the non-overlapping area.

The spatial resolution of the computational grid should be suﬃcient to resolve relevant de-

tails of the wave ﬁeld. Usually a good choice is to take the resolution of the computational

grid approximately equal to that of the input (bottom / current) grid.

SWAN may not use the entire user-provided computational grid if the user deﬁnes ex-

ception values on the depth grid (see command INPGRID BOTTOM) or on the curvi-linear

computational grid (see command CGRID). In such a case, a computational grid point is

either

• wet, i.e. the grid point is included in the computations since it represents water; this

may vary with time-dependent or wave-induced water levels or

• dry, i.e. the grid point is excluded from the computations since it represents land

which may vary with time-dependent or wave-induced water levels or

• exceptional, i.e. the grid point is permanently excluded from the computations since

it is so deﬁned by the user.

If exceptional grid points occur in the computational grid, then SWAN ﬁlters the entire

computational grid as follows:

剩余118页未读，继续阅读

weixin_41919006

粉丝: 0
资源: 1

SWAN指南：输入设置与变量输出详解

SWAN用户手册不完全版.pdf

最新版swan近岸海浪模式的程序用户手册及相关实例

SWAN Monitor AMI LineTOC分析仪表英文手册.pdf

swan海洋模式手册

swan波浪模块下载

WAVEWATCH3对比于SWAN的优点

swan海浪41.45怎么用

colorScheme=swan

tom swan's gnu c++ ii c++ fundamentals for linux pdf

cha=yt-uint8(qnoise); he=sum(sum(cha)); avg=he/(m*n); wucha=cha-avg; result1=(sum(sum(wucha.^2)))/(m*n); if result1==0 disp('swan图均方误差');result2=0 else disp('swan图均方误差');result2=sqrt(result1) end

最新资源

cha=yt-uint8(qnoise); he=sum(sum(cha)); avg=he/(mn); wucha=cha-avg; result1=(sum(sum(wucha.^2)))/(mn); if result1==0 disp('swan图均方误差');result2=0 else disp('swan图均方误差');result2=sqrt(result1) end