树的数据结构与生成树算法
下载需积分: 0 | PPTX格式 | 2.78MB |
更新于2024-06-18
| 29 浏览量 | 举报
"11 树.pptx"
在图论中,树是一种特殊的图结构,其定义为没有回路的连通图。这意味着在树中,任意两个顶点之间有且仅有一条路径,这与有环的图形成了鲜明对比。树的特性包括:
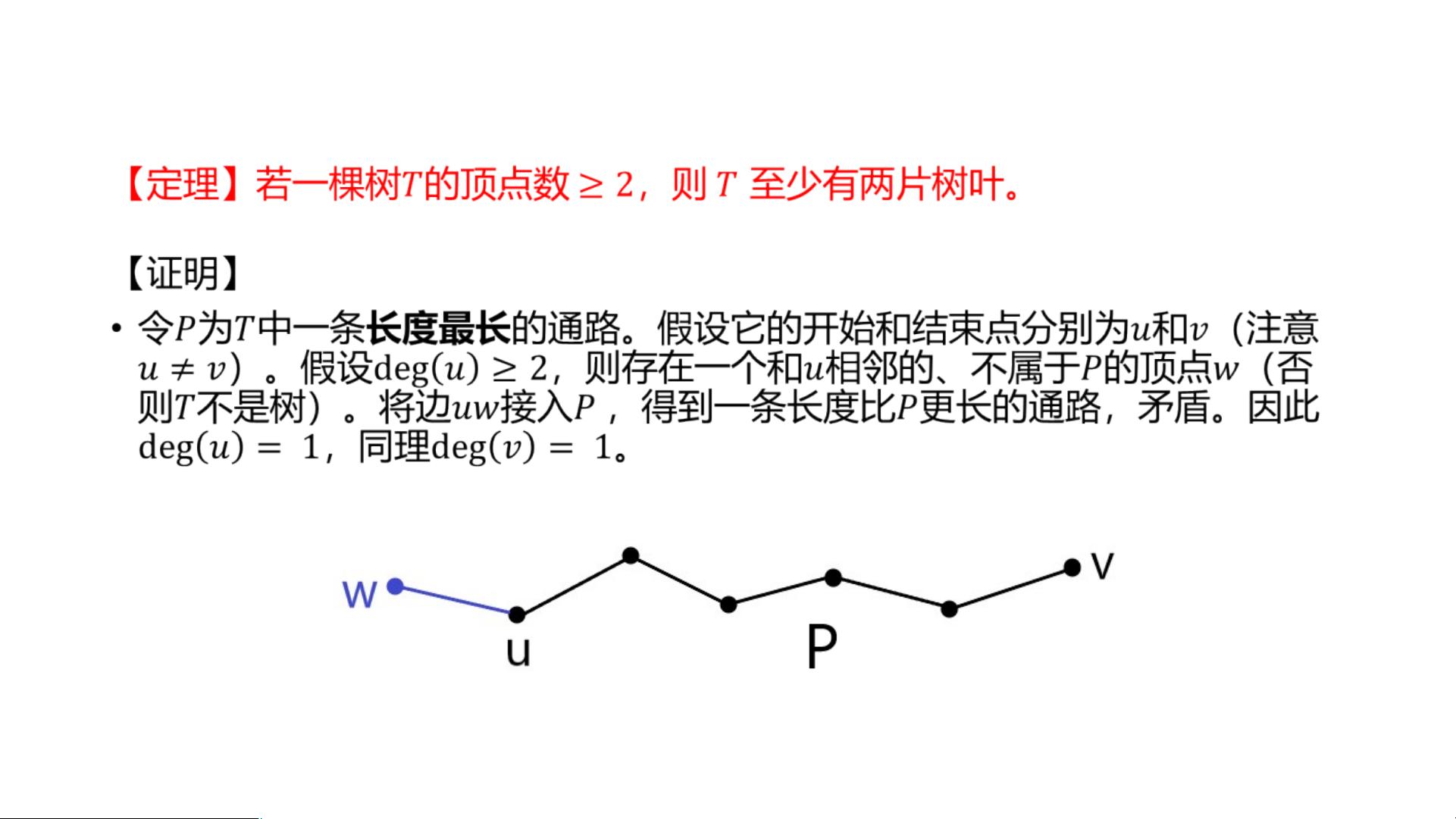
1. 树叶(终端节点):在树中,那些度数为1的顶点被称为树叶,也就是只有一个邻接点的节点。树叶通常被视为树的末端。
2. 树的性质:一棵树的顶点数V与边数E之间的关系是 E = V - 1,这是树的基本性质之一。此外,树中任何两个顶点间都有唯一的一条路径。
3. 标号图:为了便于区分图中的各个顶点,我们可以在图上给顶点分配不同的标记,如数字或字母,这样的图称为标号图。如果两个标号图中相同标记的顶点可以一一对应,那么这两个标号图就是同构的,即它们的结构是相同的。
4. 生成树:在图G中,如果删除若干边后,剩下的边仍然构成一棵树,且包含了图G的所有顶点,这样的树称为G的生成树。生成树可以有多种,比如通过深度优先搜索(DFS)或宽度优先搜索(BFS)可以构建出不同的生成树。
5. 生成树的计数:对于特定的图,可能存在多种生成树。研究生成树的计数可以帮助我们理解图的结构和性质。
6. 有根树:在树中,如果我们指定一个特定的顶点作为树的根,那么其他顶点相对于这个根就有了层次关系。例如,某个顶点的父母、祖先、后代和子树的概念都源于有根树。
7. 二叉树:在计算机科学中,二叉树是一种特殊的树形数据结构,每个节点最多有两个子节点,分为左子节点和右子节点。二叉树常用于数据的检索、排序等操作。
8. 前缀码:在二叉树编码中,前缀码是一种编码方式,其中任何编码都不会是另一个编码的前缀。这样可以确保编码的唯一性,避免歧义。例如,使用前缀码进行文本压缩,可以有效减少存储空间。
9. Huffman编码:Huffman编码是一种优化的前缀码,适用于频率不均匀的数据。它根据字符出现的频率动态构建最小带权路径长度的二叉树,频率高的字符获得较短的编码,从而实现数据的高效压缩,且无信息丢失。
10. Huffman算法:Huffman算法通过不断地合并频率最低的两个节点来构建Huffman树,直至只剩下一个节点,这个过程反映了贪心策略,但能保证得到最优的前缀码。
11. 深度优先搜索(DFS):DFS是一种遍历或搜索树或图的方法,从根节点开始,沿着路径深入探索,直到达到叶子节点,然后回溯到之前的节点继续搜索。
12. 宽度优先搜索(BFS):BFS是另一种遍历方法,它从根节点开始,优先访问所有距离根更近的节点,然后再访问距离更远的节点,形成一层一层的遍历。
这些概念和算法在计算机科学和图论中扮演着重要角色,广泛应用于数据结构、算法设计、网络路由、编译器设计、图形处理等领域。理解和掌握这些知识对于解决实际问题至关重要。
相关推荐






2301_80444279
- 粉丝: 0

最新资源
- Linux系统3D驱动及固件更新包发布
- 免费下载树形三项项目罗列PPT图形
- 解压BIOS工具:UIso9cn971使用教程与技巧
- 欧姆龙NA系列人机界面技术参数与选型样本下载
- ABP框架系列教程:深入理解H+UI及API集成
- 全面解读知识管理报告的核心价值与实用指南
- WPR_Hist脚本:探寻MetaTrader价格顶底分析
- 深入解析Amazon Linux 2的Dockerfile构建
- React Native中3D建模的轨道控制实践指南
- MVC模式实现的Web图书管理系统开发指南
- Vue.js devtools 4.1.4版Chrome插件安装指南
- 易语言实现ACCESS数据库操作的完整示例教程
- 探索商业智慧:哈佛商业评论精选集
- 折叠效果并列关系PPT图形下载教程
- Altium和Protel必备电子元器件封装库下载
- 深入解析非负矩阵分解算法及其应用