模板匹配算法详解与实现

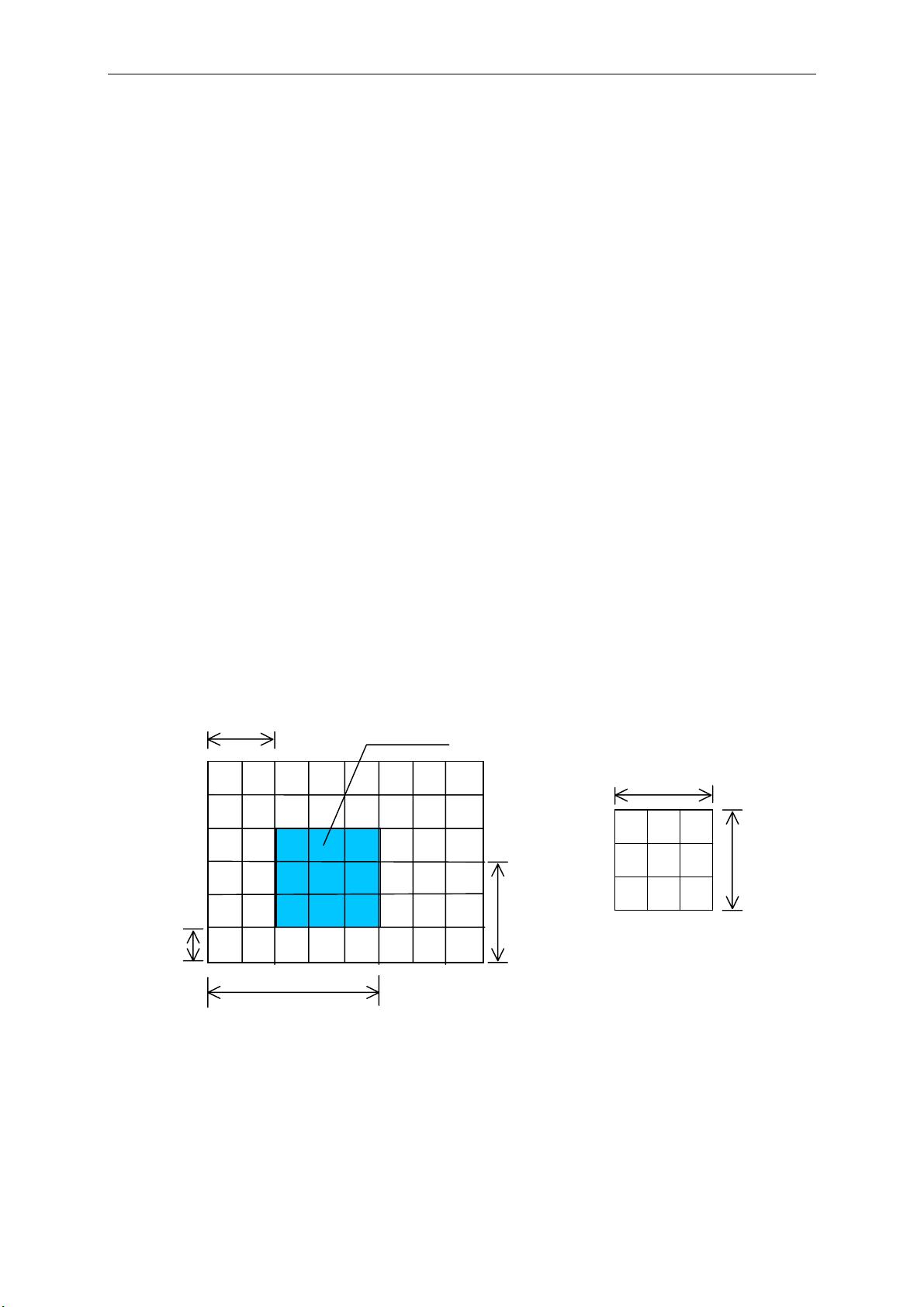
"模板匹配算法介绍与代码" 模板匹配是一种图像处理技术，它在计算机视觉和图像分析领域中广泛应用于目标检测和识别。这个过程基于一个假设：已知一个小图像（模板），要在更大的图像（被搜索图）中寻找与模板相同或者高度相似的目标。模板匹配的目标是确定模板在被搜索图中的精确位置。 模板匹配的基本步骤如下： 1. **定义模板**：模板是一张小图像，通常代表我们想要在大图像中查找的目标。它的尺寸、方向和图像特征需要与目标一致。 2. **匹配过程**：将模板T(m×n像素)平移覆盖到被搜索图像S(W×H像素)的不同区域，形成子图Sij。子图的左上角坐标为(i, j)。搜索范围限定在不超出图像边界的情况下，即1≤i≤W-M和1≤j≤H-N，其中M和N分别为模板的宽度和高度。 3. **相似度计算**：通过比较模板T与子图Sij的相似性来评估匹配程度。常用的相似度度量方法是计算两者的互相关或差平方和。对于8位图像，每个像素用1个字节表示，可以使用以下公式： \[ D = \sum_{n=1}^{N}\sum_{m=1}^{M}(T(n,m)-S_{ij}(n,m))^2 \] 其中，D表示差异的平方和，第一项表示子图的能量，第三项表示模板的能量，而第二项是模板和子图的互相关。当模板与子图匹配时，互相关的值最大。 4. **归一化相关系数**：为了消除能量项的影响，通常会归一化这个值，得到相关系数： \[ R = \frac{\sum_{n=1}^{N}\sum_{m=1}^{M}(T(n,m)\cdot S_{ij}(n,m))}{\sqrt{\sum_{n=1}^{N}\sum_{m=1}^{M}T^2(n,m)}\cdot \sqrt{\sum_{n=1}^{N}\sum_{m=1}^{M}S_{ij}^2(n,m)}} \] 相关系数R的值在-1到1之间，值接近1表示模板与子图匹配良好，而接近-1则表示匹配较差。 在实际应用中，模板匹配可能需要考虑以下因素： - **模板尺度变化**：目标在被搜索图像中可能以不同大小出现，因此需要进行多尺度匹配。 - **旋转不变性**：目标可能以不同的角度出现，因此需要设计旋转不变的模板匹配方法。 - **光照和噪声影响**：图像质量、光照变化以及噪声可能影响匹配结果，需要使用稳健的算法来应对这些因素。 - **计算效率**：大规模图像的模板匹配可能会非常耗时，因此优化算法和使用并行计算策略是必要的。 模板匹配是计算机视觉领域的一个基础工具，适用于人脸识别、物体检测、图像检索等多种应用场景。然而，它也有一些局限性，例如容易受到背景干扰，对复杂场景的适应性较弱。因此，现代计算机视觉研究通常会结合其他技术，如深度学习和特征提取，来提高目标检测的准确性和鲁棒性。