马尔科夫决策过程详解：构成、稳态与无限步数MDP策略

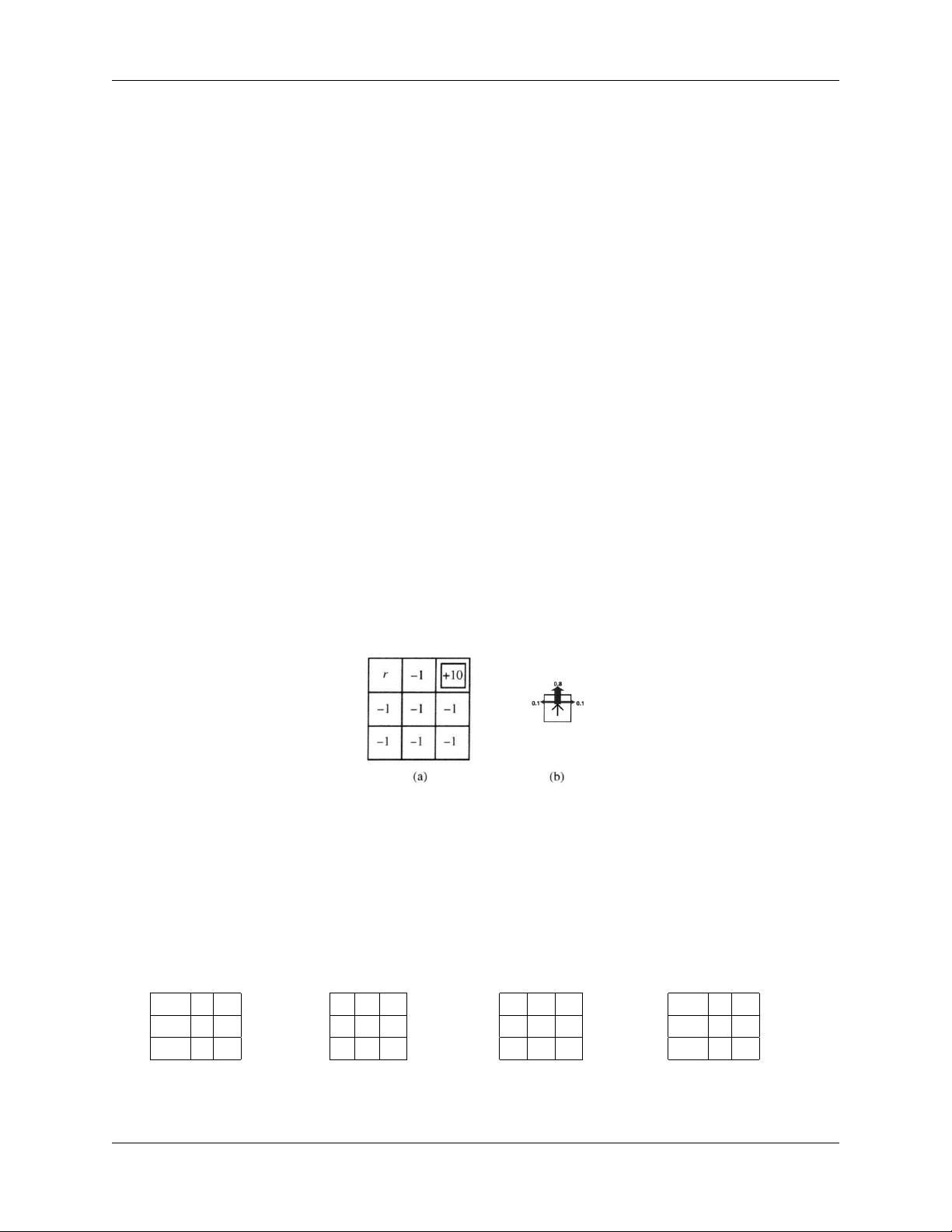
本篇文档是关于智能系统设计与应用的课后练习参考答案，主要涉及马尔科夫决策过程（Markov Decision Process, MDP）的相关概念和问题解答。马尔科夫假设的核心在于状态转移只依赖当前状态和上一步的行动，而不考虑过去的历史。一个完整的MDP包含四个基本元素： 1. 状态集合S：代表所有可能的状态，如文中提到的"high"、"low"等，对于吸尘机器人来说可能代表清扫或待机状态。 2. 行动集合A：表示在每个状态下可以选择的动作，如吸尘机器人的问题中，可能是"search"（搜索）、"wait"（等待）和"recharge"（充电）。 3. 转移函数T(s′|s,a)：描述了在执行某个动作a后，从状态s转移到下一个状态s'的概率分布。 4. 奖励函数R(s,a)：给出了在执行某个动作a时，在当前状态s获得的即时回报。 稳态MDP 是指转移函数和奖励函数不随时间变化的MDP，它可以通过决策网络表示，如图1所示，其中每个节点代表一个状态，边上的箭头和权重表示了状态转移的概率和奖励。 问题2探讨的是无限步数MDP中的策略选择，根据折扣因子γ的不同，确定性策略πleft和πright的优劣。当γ=0时，没有未来奖励的影响，所以总是选择左行动为最优；当γ=0.5时，两个策略都同样好；而当γ=0.9时，右行动由于其长远考虑的特性变得更优。 问题3涉及计算吸尘机器人的最优状态值函数，即贝尔曼最优方程。对于high和low两种状态，分别求解最优状态值，这涉及到动态规划的过程，通过迭代更新状态值，直到达到最优解。贝尔曼方程给出了状态价值函数的递归定义，涉及了概率转移和奖励的加权平均。 本文档提供了对马尔科夫决策过程基础理论和具体应用实例的深入解析，对于理解和设计依赖状态转移和决策策略的智能系统具有重要的参考价值。