概率论与连续型随机变量讲义

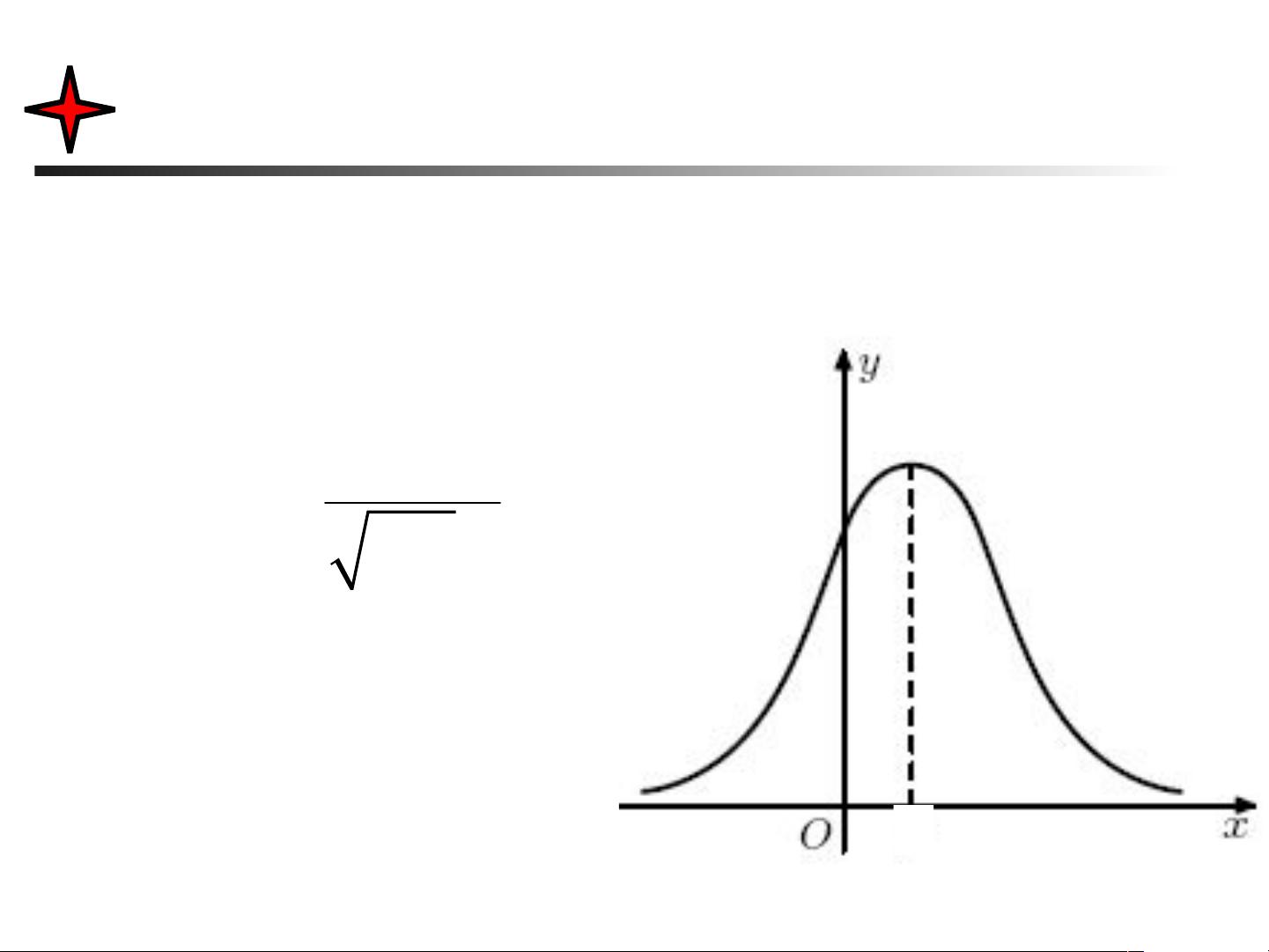
"这是一份概率论基础讲义的PPT，主要涵盖了连续型随机变量和正态分布的概念，特别强调了概率密度函数的定义以及正态分布的性质。" 在概率论中，随机变量是统计学中的核心概念，它表示实验结果的一种量化表现。当我们谈论连续型随机变量时，意味着变量可能取到无限多个可能的值，而不是离散的几个值。一个随机变量X被定义为连续型，当其分布函数F(x)满足以下条件：存在一个非负可积函数p(x)，使得对于所有的x，F(x)可以通过对p(x)在整个实数轴上积分得到。这个函数p(x)就是随机变量X的概率密度函数，记作X~p(x)。概率密度函数的性质是，它的积分等于1，即 ∫(-∞, ∞) p(x) dx = 1，并且任何区间A上的概率可以通过该区间上的概率密度函数积分得到，即 P(X∈A) = ∫_A p(x) dx。 正态分布，又称为高斯分布，是概率论中最重要、最广泛使用的连续分布之一。它有一个显著的特性，即它的密度函数呈钟形曲线，对称于均值μ，并且方差σ²决定了曲线的宽度。标准正态分布是一个特殊的正态分布，其均值μ为0，方差σ²为1。其概率密度函数为 f(x) = (1/√2π) * e^(-x²/2)。正态分布的分布函数，也称为累积分布函数，可以用来计算小于或等于某个值的概率。对于一般正态分布X ~ N(μ, σ²)，分布函数F(x)可通过标准正态分布函数进行转换求得。 正态分布的验证通常涉及对其概率密度函数的积分，例如，为了验证标准正态分布的归一性，即积分面积为1，我们需要证明 ∫(-∞, ∞) (1/√2π) * e^(-x²/2) dx = 1。这通常通过使用积分变换，如极坐标变换来完成。例如，将直角坐标系下的积分转化为极坐标系下的积分，然后再进行计算，以证明其积分确实等于1。 这份讲义通过详细的公式推导和解释，帮助学习者理解并掌握连续型随机变量特别是正态分布的基本理论与应用，是概率论初学者的一个良好参考资料。