有限数据统计处理：理解样本与置信区间

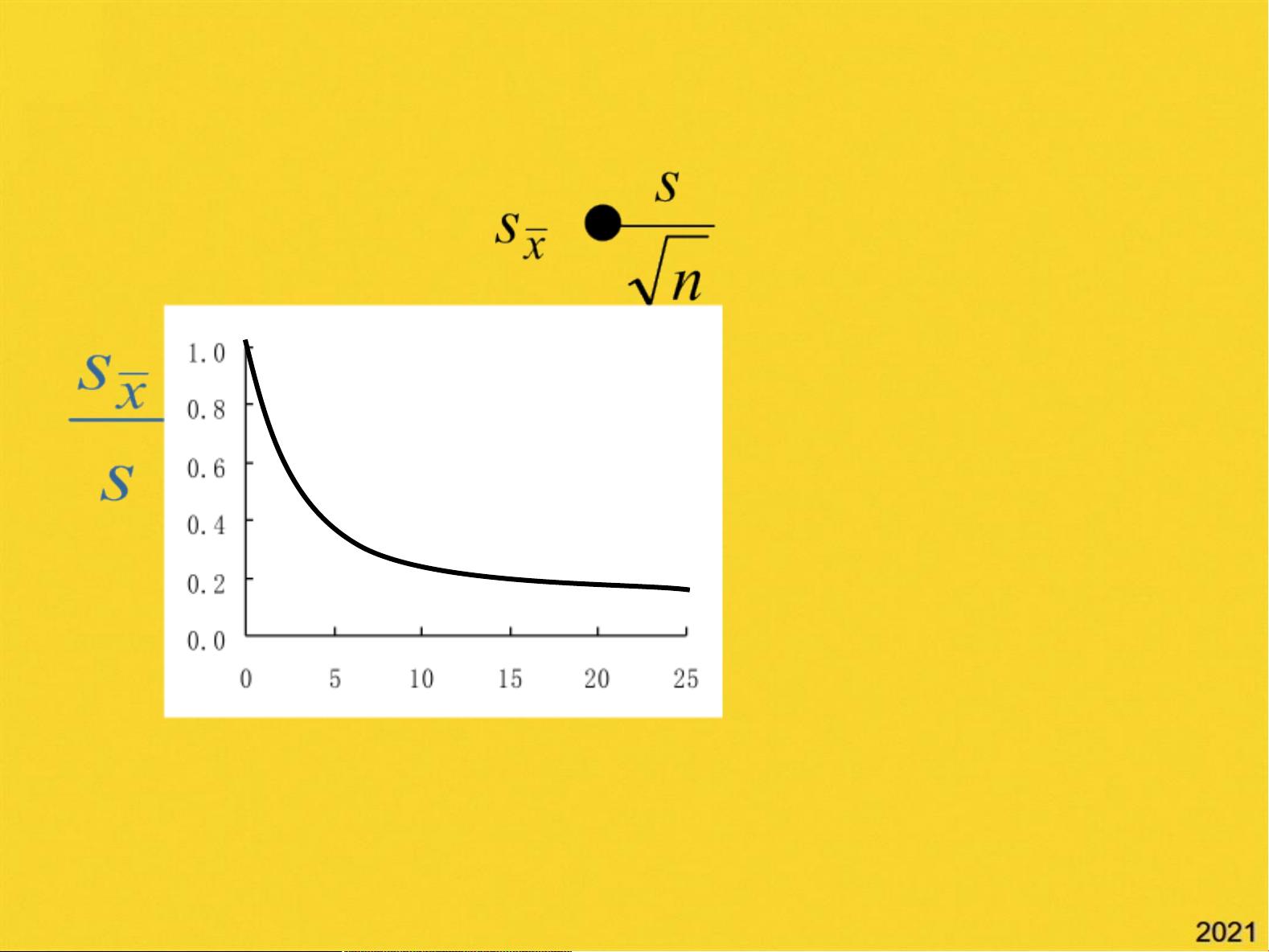
"有限数据统计处理(共44张PPT)精选.pptx" 这份资料详细介绍了有限数据的统计处理方法，主要包括总体、个体、样本的概念，置信区间的计算，以及数据集中趋势和分散程度的度量。在统计学中，总体是指研究对象的全体，比如所有学生；个体则是组成总体的每一个单独元素，如单个学生；样本是从总体中抽取的一部分，用于代表总体，如选取的一部分学生。样本容量则是样本中包含的个体数量。 置信区间是统计推断中的重要概念，它表示了一个估计值可能落在的范围，具有一定的置信水平。例如，以95%的置信水平意味着我们有95%的把握认为总体参数在这个区间内。在实际应用中，如果要判断某个参数（如均值）是否发生变化，可以通过计算置信区间并比较不同样本的均值来决定。 在有限次测量的情况下，测量值倾向于聚集在平均值附近，而无限次测量时，测量值则会趋向于总体平均值。例如，若要估计一所大学全体学生平均每天参加体育锻炼的时间，可采用t分布统计量，因为样本量通常小于总体大小，且已知总体方差。 数据的集中趋势通常由期望值（平均值）、中位数等指标来衡量，表示数据集的“中心”位置。数据的分散程度则反映数据的离散程度，常用指标包括极差、偏差、平均偏差等。极差是最大数据与最小数据的差，平均偏差考虑了每个数据点与平均值的距离，而相对平均偏差则是平均偏差与平均值的比值，常用来衡量数据的相对离散程度。 在处理有限数据时，除了计算估计值，还需要进行显著性检验，以确定观测到的差异是否是由随机误差引起还是真实存在的系统误差。例如，通过Dixon检验统计量和临界值可以判断是否存在异常值。如果显著性检验结果表明存在显著差异，则表明所研究的参数（如平均值）可能与假设的不同。 这份PPT资料涵盖了统计学中基础但重要的概念，包括总体与样本的区分、置信区间的构建、数据集中趋势和分散程度的度量，以及如何在有限数据条件下进行统计推断和决策，对于理解和应用统计方法具有指导意义。