最大熵模型与EM算法：信息论基石与机器学习应用

最大熵模型与EM算法是统计学习和信息论中的两种重要方法，它们在机器学习领域广泛应用。本资源主要涵盖了以下几个核心知识点： 1. 统计学习基础： - 后验概率：在机器学习中，后验概率P(Y|X)表示在观察到特征X的情况下，某个标签Y发生的概率，是模型预测的核心概念。 - 极大似然法 (MLE)：这是最常用的参数估计方法，基于已发生的事件最大概率的原则，寻找数据集上的最优模型参数。 2. 信息论基础： - (互)信息：衡量随机变量之间的依赖关系，是评估信息传递量的关键指标。 - 熵和条件熵：熵表示随机变量自身的不确定性，条件熵则是给定另一个变量后的不确定性。 - 交叉熵和相对熵：用于比较两个概率分布的差异，常用于模型评估和优化。 3. 最大熵模型： - 凸优化理论：利用数学工具证明最大熵模型的优化问题可以通过凸优化方法求解，最大化模型的熵可以保证模型的复杂度不会过度拟合。 - 与极大似然法的关系：最大熵模型并非总是提供最高似然估计，但通过约束条件下的优化，它能在保持简单性的同时，达到良好的预测性能。 4. EM算法： - GMM (高斯混合模型) 实例：EM算法是一种迭代优化算法，特别适用于处理带有隐变量的数据，如GMM中的未观测状态。 - MLE推导EM：EM算法通过交替最大化期望似然函数（E步）和最大化对数似然函数（M步），在无完全观测数据的情况下，估计模型参数。 5. 监督学习与无监督学习： - 有监督学习：利用带标签的数据进行模型训练，如最大熵模型在分类任务中的应用。 - 无监督学习：在没有标签数据的情况下，如GMM进行密度估计和聚类。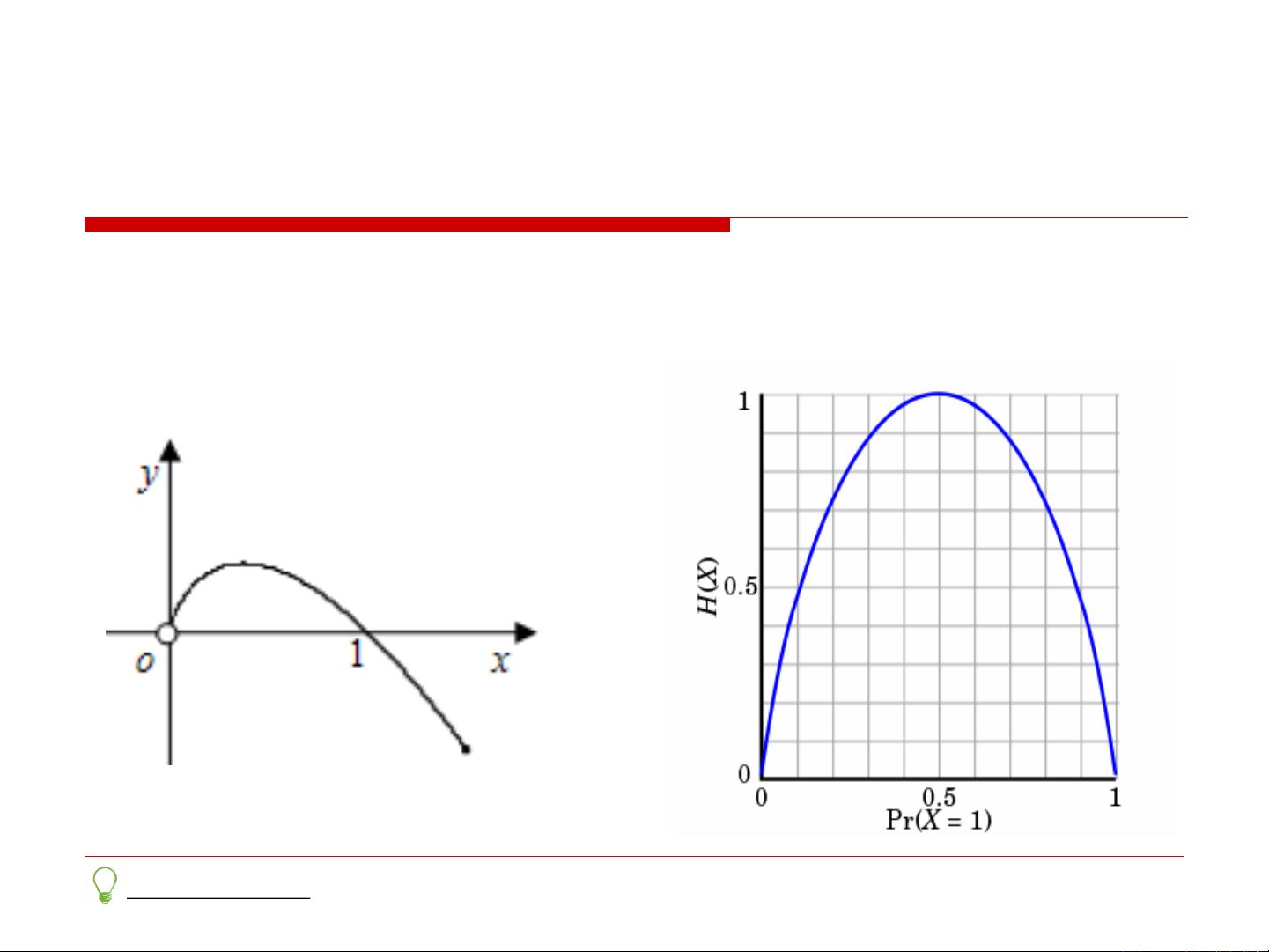 6. 自信息与熵： - 自信息 i(x) = -log(p(x)) 表示一个事件的概率p(x)的负对数，体现了信息量。 - 熵是自信息的期望值，它衡量了随机变量的不确定性，对于均匀分布，熵达到最大，表示最高的不确定性。 7. 实际应用举例： - 白富美相亲网的例子：展示了最大熵模型或EM算法在实际场景中的预测和决策过程。 通过理解并掌握这些知识点，学习者能够构建有效的统计模型，并在实际机器学习项目中灵活运用最大熵模型和EM算法。