动态传染病与战争模型：微分方程建模详解

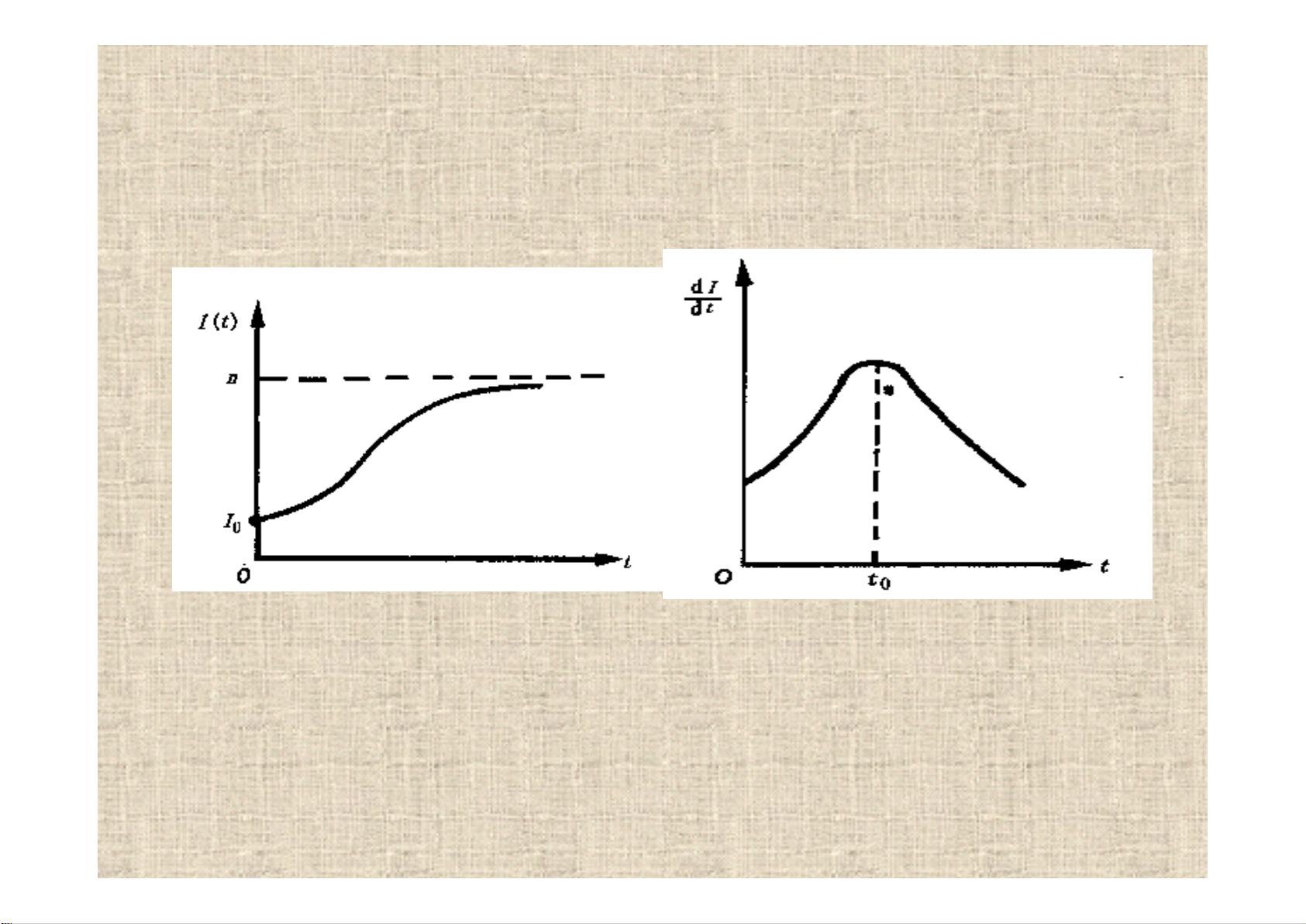
"动态微分方程模型课程资源包含了关于传染病和战争模型的深入讨论，适合学习不同技术领域的学生和进阶学习者。课程主要围绕传染病的数学模型构建展开，以实际问题为导向，如如何预测传染病的流行趋势。 首先，课程介绍了四种传染病模型。第一个模型假设一人患病期间不会死亡，且传染率恒定，建立了简单的线性微分方程，表示病人数随时间的增长。然而，这个模型忽略了实际中病人数可能受总人口数量变化的影响，即k值应随时间变化。因此，课程进一步发展了模型二，引入健康人数S(t)，并将传染率k与健康人数成正比，使得模型更接近现实情况。 模型二假设总人口固定，病人生存期不考虑死亡，且每个病人在单位时间内传染的比例与健康人数成比例。改进后的模型解决了初始模型中病人数无限增长的问题，给出了更为合理的增长趋势。通过这些模型，学生们可以理解传染病传播的数学原理，以及如何根据实际情况调整模型参数。 此外，课程还鼓励学习者通过解决实际问题来深化理解，例如分析不同阶段的k值变化规律，以及如何在模型基础上进行扩展和修改，以适应不同的传染病情况。整个课程资源不仅提供源码，还有详尽的理论讲解和实例分析，旨在培养学生的数学建模能力和问题解决能力，对于项目设计、毕设、课程作业和科研实践都有很高的实用价值。" 在这个资源中，你不仅能学到微分方程在传染病模型中的应用，还能锻炼逻辑思维和问题解决技巧，同时了解如何根据数据和实际情况优化模型，这对于IT专业人士来说是一项宝贵的学习材料。