直方图均衡化原理与OpenCV实现解析

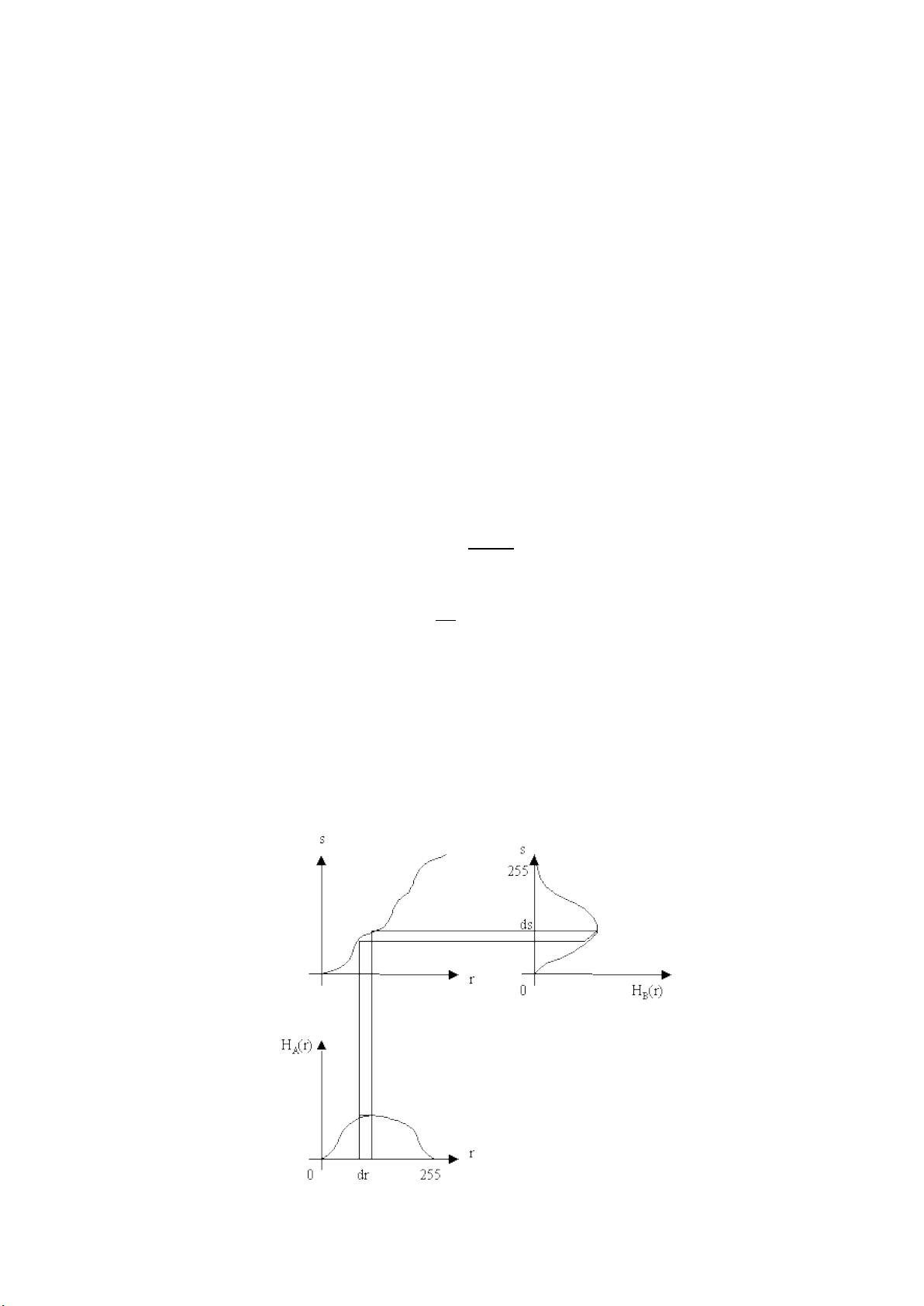
"直方图均衡化是一种图像处理技术，用于增强图像的对比度，尤其在图像对比度较低的情况下效果显著。它通过调整图像的灰度级分布，使得图像的直方图更加均匀，从而使得图像中的细节更加清晰。本文将介绍直方图均衡的原理及其在OpenCV中的实现。 直方图均衡化的核心思想是将原图像的灰度分布转化为一种新的分布，使得每个灰度级上的像素数量大致相同。首先，我们需要理解直方图的概念，它是统计图像中每个灰度级出现的频率。对于一个灰度范围在[0, L]的图像A，其直方图Hᴬ(r)表示了灰度级r对应的像素数量。 接下来，我们进行概率分析。将图像A的直方图归一化，得到概率密度函数p(r) = Hᴬ(r)/A₀，其中A₀是图像A的总像素数。再根据概率分布函数P(r) = 1/A₀ ∫Hᴬ(r) dr from 0 to L，可以推导出灰度变换函数s = T(r)。 在保持直方图面积不变的前提下，我们希望输出图像B的直方图Hᴮ(s)与输入图像A的直方图Hᴬ(r)之间有恒定的关系。因此，可以通过微分求解出灰度变换函数T(r)。最终得到的变换函数形式为s = C × P(r)，其中C是一个常数，P(r)是输入图像的概率分布函数。为了确保s的取值范围在[0, L]内，常数C等于L，所以灰度变换函数变为s = L × P(r)。 在实际的离散图像处理中，我们可以使用累积分布函数(CDF)来近似概率分布函数，得到灰度变换的离散形式s = T(r_k) = C × P(r_k)，其中P(r_k)是累加到灰度级r_k的概率。 在OpenCV中实现直方图均衡化通常包括以下步骤： 1. 计算图像的直方图并进行归一化，以获取概率分布。 2. 计算累计概率分布函数，这将给出灰度变换函数s = T(r)。 3. 应用这个变换函数，将原图像的每个像素的灰度值替换为新的灰度值s。 以上述代码为例，通过`cv::calcHist`计算直方图，然后利用累积分布函数实现灰度变换，最后用`cv::LUT`函数快速应用变换到图像上。 直方图均衡化是一种有效的图像预处理技术，可以显著提升图像的视觉效果，尤其是在低光照或对比度较弱的场景下。OpenCV提供了便捷的接口和函数来实现这一过程，使得开发者能够轻松地将这种技术应用于各种图像处理项目中。"