伽玛函数：阶乘的超越之旅

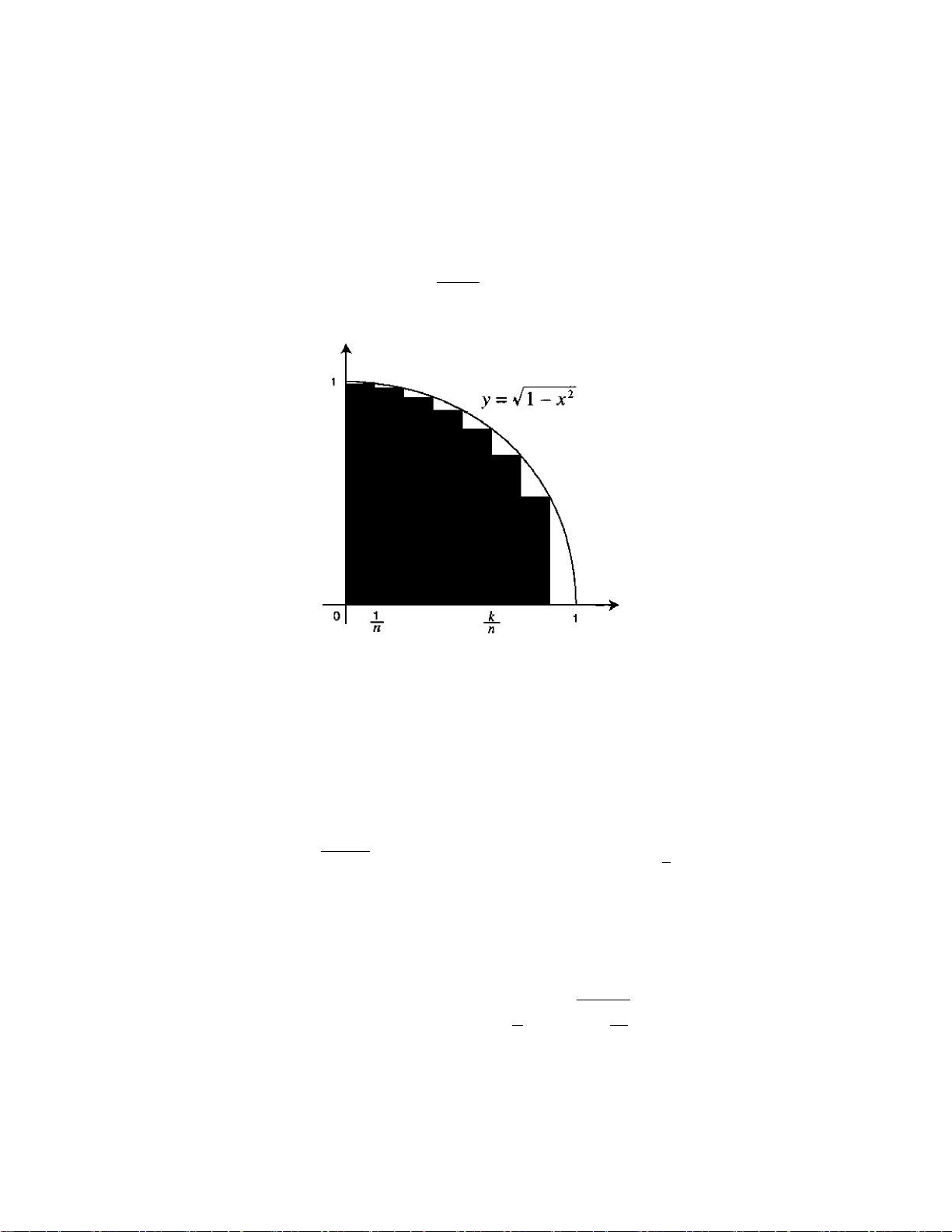
"神奇的伽玛函数.pdf" 这篇文档主要探讨了伽玛函数这一数学概念，它是数学中的一个重要工具，尤其在高等数学中占有显著地位。伽玛函数通常表示为Γ(x)，其定义是一个积分形式，即Γ(x) = ∫∞0tx−1e−tdt，它是一个超越函数，而非初等函数。尽管其定义看起来并不直观，但伽玛函数实际上是阶乘函数在实数范围内的推广。 文档提到了伽玛函数的一个关键性质，即递归关系Γ(x+1)=xΓ(x)。这个性质使得伽玛函数与阶乘函数建立了联系，尤其是当x为正整数n时，Γ(n)=(n−1)!。这种推广允许阶乘的概念扩展到所有正实数，甚至包括负实数的一部分。 伽玛函数在多个数学领域中扮演着重要角色，包括微积分、概率论、偏微分方程、组合数学以及数论。在概率论中，伽玛函数与伽马分布紧密相关，这是一个在统计建模中常见的连续概率分布。在物理领域，伽玛函数也有广泛的应用，尤其是在量子力学和热力学的研究中。 文档还提到了伽玛函数的历史，其起源与数学家们的探索密切相关。伽玛函数的诞生涉及到了一系列的数学发现和理论发展，其中包括沃利斯公式，这是在无意识中发现的一个与伽玛函数相关的数学结果。此外，文档还讨论了伽玛函数的近似与插值艺术，这是数值计算中处理伽玛函数的一种技术。 伽玛函数的神奇之处在于，尽管其定义看起来复杂，但在解决实际问题中却展现出惊人的简洁性和实用性。通过对伽玛函数的学习，我们可以深入理解数学的内在联系，以及它如何在不同学科间架起桥梁。 文档最后部分可能包含了伽玛函数在随机数学中的应用，以及作者对伽玛函数的个人理解和推荐的相关阅读材料，这些内容将为读者提供更全面的视角来研究和欣赏伽玛函数的魅力。通过这份文档，读者不仅可以了解到伽玛函数的基本性质，还能体会到数学探索的过程以及数学在现实世界中的深远影响。