半角旋转模型解析：线段关系证明与几何变换

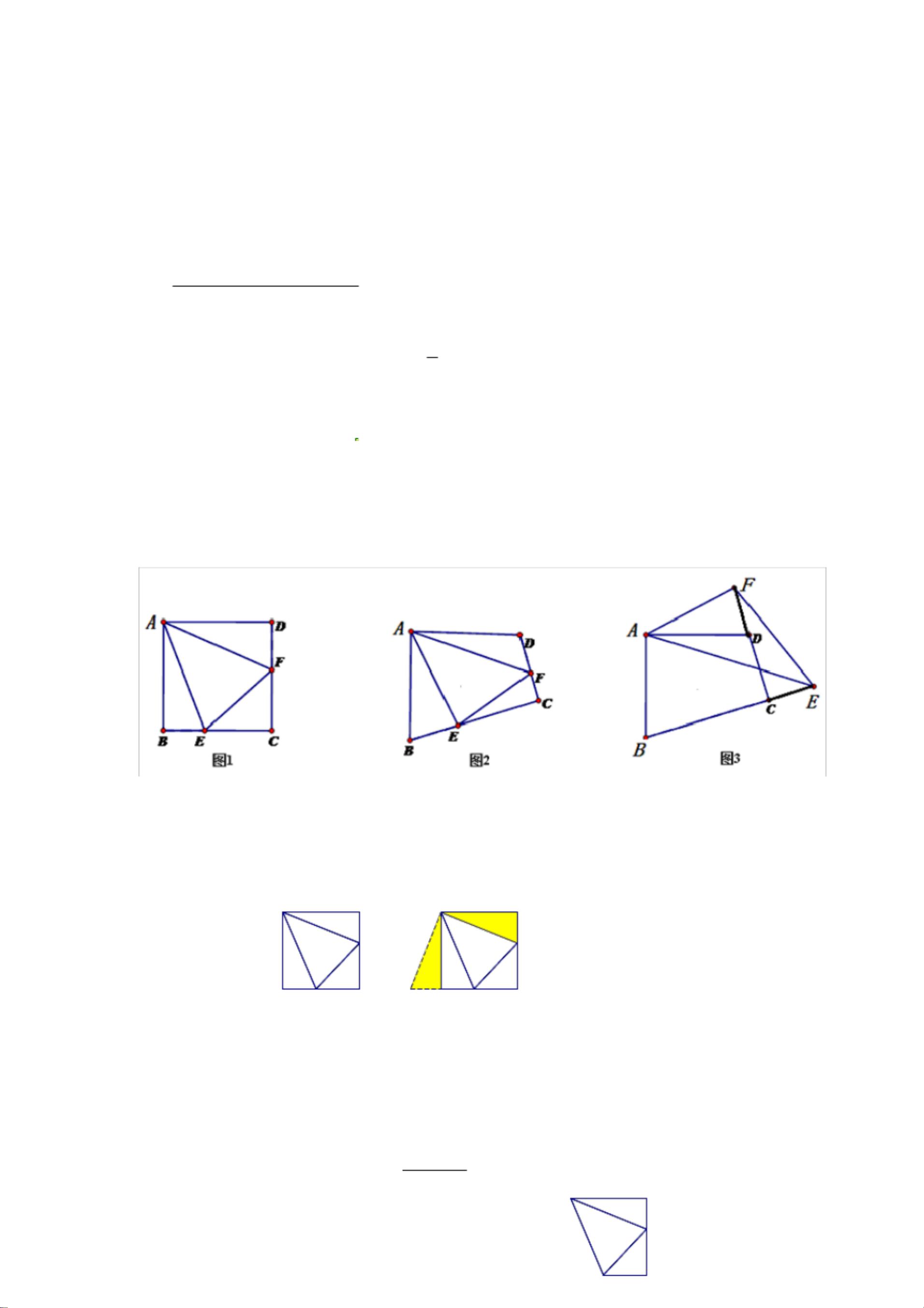
半角旋转模型(完整资料).doc.pdf是一份详细探讨几何学中半角旋转概念及其应用的文档。该文档主要关注三个关键部分：三垂直模型、旋转相似模型，以及在具体几何图形中的应用。 1. 三垂直模型：文档首先介绍了如何通过三垂直模型来理解旋转，即在一个图形中，如果存在一条直线，使得图形沿该直线旋转一定角度后，原图形与新图形的对应边垂直，那么这个旋转就是半角旋转。例如，正方形ABCD中，通过将△ADE绕点A顺时针旋转90°得到△ABG，使得GF与DE+BF重合，这是三垂直模型在实际问题中的运用。 2. 旋转相似模型：文档探讨了旋转相似性，即两个图形经过相同的角度旋转后，它们的形状保持不变，只是位置发生了改变。文档中的例子涉及在四边形ABCD中，当旋转角度变化时，某些线段关系是否仍然成立，比如∠EAF的角度变化对BE、DF与EF的关系是否有影响。 3. 具体问题分析：文档深入解析了两个具体问题。第一个问题是关于直角梯形ABCD，其中AD∥BC且∠D=90°，通过旋转找到线段BE的长度。第二个问题是坐标系中的几何变换，涉及到动态点B和正方形ABCD的位置关系，以及C点坐标的表达。 4. 旋转角度和线段长度计算：文档中还涉及了如何通过旋转确定旋转后的线段长度，如∠GAF的度数计算，以及根据旋转角度和已知条件求解未知线段长度。 5. 正方形旋转后的性质：最后，文档讨论了正方形ABCD绕点A旋转时，其边与边的交点关系变化，以及正方形的对角线MN与旋转后的边的关系。 总结来说，这份文档提供了一套完整的半角旋转模型理论和实际问题解决策略，适用于初高中数学教学或相关专业人员学习几何变换。通过阅读和理解这份文档，读者可以掌握旋转在几何图形中的重要作用，以及如何利用它来解决问题。