二维稳态泊松方程的有限差分解法

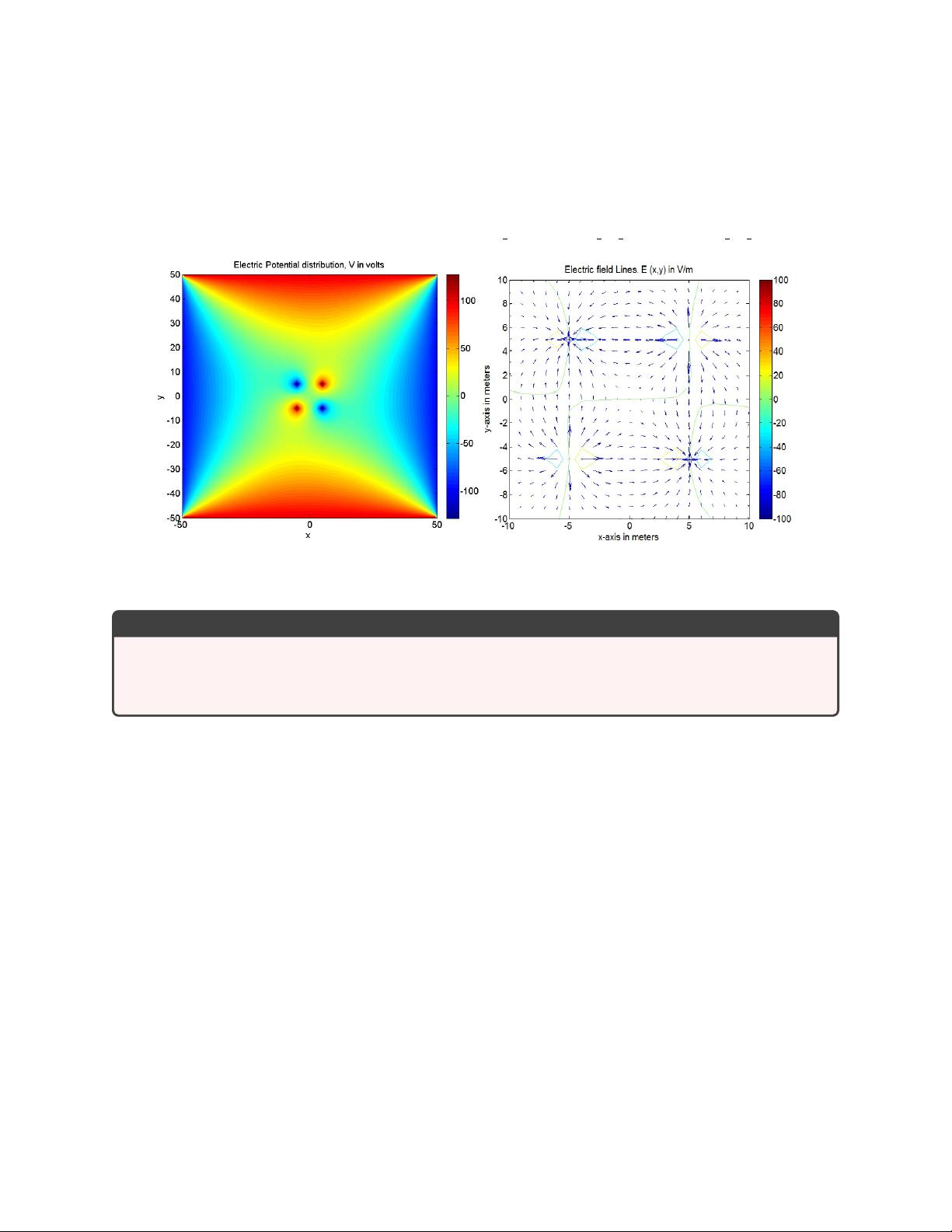
"这篇文档主要介绍了二维稳态泊松方程的求解方法，结合实例讲解了如何使用有限差分法构建方程模型，设置相应的线性系统，并对近似解进行绘制和误差计算。文档源自MATH1091课程，讨论了从一维空间向二维空间扩展的问题，特别关注在二维矩形区域内的应用。" 泊松方程在物理学、工程学和数学等领域中有广泛的应用，特别是在电磁学中，电势问题就是一个典型的泊松问题。稳态泊松方程是描述没有时间变化的物理现象，例如在静电力场中的电势分布。该方程通常写为： ∇²φ = -ρ/ε₀ 其中，φ 是电势，ρ 是电荷密度，ε₀ 是真空电容率，∇² 是拉普拉斯算子。 在二维矩形区域中处理稳态泊松问题时，我们首先将连续的偏微分方程离散化为有限差分方程。这通常涉及将空间区域划分为网格，并用网格节点上的值近似原方程的解。对于边界条件，可能有 Dirichlet 条件（指定边界上的值）或 Neumann 条件（指定边界上的梯度）。 文档中提到的方法是建立一个线性系统，该系统由有限差分方程的离散版本构成。例如，可以使用中心差分来近似二阶导数，从而得到一组线性代数方程组。这个线性系统的矩阵通常是稀疏的，因为它大部分元素为零，这使得高效求解成为可能。 接下来，通过求解这个线性系统，我们可以得到电势在每个网格点的近似值。这通常使用迭代方法，如高斯-塞德尔迭代或雅可比迭代。一旦求得近似解，可以使用图形软件绘制电势分布图，以便直观地理解解决方案。 为了评估解的精度，文档中提到了计算近似误差的范数。常见的方法是计算残差的 L2 范数，定义为所有网格点上误差平方和的平方根。这提供了一个定量度量，用于确定解的质量和收敛速度。 在实际应用中，从一维问题扩展到二维问题增加了复杂性，但同时也增加了解决问题的灵活性。例如，可以模拟更复杂的几何形状和更丰富的物理过程。这种扩展方法也可以进一步推广到三维空间和时空变量问题，从而解决更广泛的科学和工程挑战。 该文档提供的内容详细介绍了如何运用有限差分法解决二维稳态泊松问题，包括方程的离散化、线性系统的建立、解的求解以及误差分析。这些方法对于理解和模拟二维空间中的物理现象至关重要。