H.264/AVC编码优化：基于源图像边缘特征的运动估计
需积分: 0 110 浏览量
更新于2024-11-22
收藏 401KB PDF 举报
“H.264/AVC编码算法运动估计的优化——利用源图像边缘特征”
在视频编码领域，H.264/AVC（Advanced Video Coding）标准因其高效的压缩性能而广受赞誉。该标准通过处理可变大小的运动补偿预测块并结合多个参考帧来显著提高压缩效率。然而，这种高效性的代价是计算运动估计的复杂度随着参考帧数量和交互模式数量的乘积增加而增加。
本文《H.264/AVC编码中的运动估计优化：利用源图像边缘特征》由Zhenyu Liu、Junwei Zhou、Satoshi Goto和Takeshi Ikenaga等人发表于2009年8月的IEEE Transactions on Circuits and Systems for Video Technology，深入分析了运动补偿预测误差主要由源图像中的详细纹理决定。当图像块包含丰富的纹理时，其中包含大量高频信号，这就使得可变块大小和多参考帧技术变得至关重要。
基于率失真理论，作者提出将图像块的空间均匀性视为相对于当前量化步长的相对概念。对于均匀的图像块，由于其高频信号较少，运动估计的计算可以简化，从而减少计算量。论文中提出了一种方法，通过对图像块进行边缘检测和分析，识别出那些相对均匀的区域，以便在保持编码质量的同时，降低运动估计的复杂度。
此外，论文还探讨了如何利用源图像的边缘特征来指导运动估计过程。边缘通常代表图像中的物体边界或运动变化，是运动估计中重要的线索。通过有效地利用这些特征，可以更准确地预测运动向量，进而减少错误传播，提高压缩效率。
为了优化运动估计，论文可能提出了以下策略：
1. 边缘检测和特征提取：首先，对源图像执行边缘检测，提取出关键的边缘信息，这些信息可以帮助识别出运动边界。
2. 块分类：根据边缘特征将图像块分为均匀和非均匀类别，对于均匀区域采用简化的运动估计方法。
3. 运动向量预测：基于边缘信息和块分类结果，优化运动向量的搜索策略，例如，限制搜索范围或者采用更高效的搜索算法。
4. 量化步长适应：根据图像内容和边缘特征动态调整量化步长，以平衡编码质量和计算复杂度。
这篇研究通过深入分析H.264/AVC编码中运动估计的特性，提出了利用源图像边缘特征优化运动估计的方法，旨在在不牺牲编码性能的前提下，降低编码过程的计算复杂度，这对于实时视频编码和资源有限的设备具有重要意义。
LIU et al.: MOTION ESTIMATION OPTIMIZATION FOR H.264/AVC USING SOURCE IMAGE EDGE FEATURES 1097
Camera sensor
x
s
t
(x)
s'
t
(i·u
x
)
s
t – 1
(x)
Δ
x
s'
t
(i·u
x
)
e(i·u
x
)
d
x
u
x
i
i + 1 i + 2 i + 3
Δ
x
Fig. 1. Analysis of 1-D prediction error caused by edge gradient and
displacement estimation error.
where s
t
(i · u
x
) is the edge gradient of s
t
(x) at the ith
camera sensor and the displacement estimation error
x
is
a random variable with zero mean and
x
∈ [−u
x
/2, u
x
/2].
When
x
=±u
x
/2, |e(i · u
x
)| reaches its maximum value
(u
x
·|s
t
(i · u
x
)|)/2 and when
x
= 0, |e(i · u
x
)| vanishes.
This conclusion agrees with the aliasing investigation in the
spectral domain provided in the literature [14]. Equation
(2) also interprets the necessity of MRFs during prediction
processing: If the displacement error
x,t−1
between the
current image s
t
(x) and the first previous one s
t−1
(x) is larger
than that of the kth previous image s
t−k
(x), i.e.,
x,t−k
,
s
t−k
(x) is preferred to be chosen as the prediction signal
because its prediction error coming from aliasing problem is
reduced.
In order to simplify the notations in the following discus-
sions, it is assumed that the spatial sampling intervals in x-
and y-direction are u
x
= u
y
= 1. From (2), it is convenient
to derive the 2-D prediction error in one pixel
e(i, j) ≈
x
(i, j) ·
∂s
t
(i, j)
∂x
+
y
(i, j) ·
∂s
t
(i, j)
∂y
. (3)
If it is assumed that
x
(i, j) and
y
(i, j) are independent,
E(
x
) = E(
y
) = 0, and E(
2
x
) = E(
2
y
) = σ
2
, the variance
of e(i, j), i.e., σ(i, j), is written as
σ
2
(i, j) = σ
2
∂s
t
(i, j)
∂x
2
+
∂s
t
(i, j)
∂y
2
. (4)
Using the prediction error variance of one pixel (4), the
prediction error power of an image block can be deduced as
i, j
σ
2
(i, j) = σ
2
i, j
∂s
t
(i, j)
∂x
2
+
∂s
t
(i, j)
∂y
2
(5)
where (i, j ) ∈ block.
Like the spectral analysis represented by (1), (5) also
indicates that the prediction error power is determined by
the image features and the displacement estimation error.
Additionally, the spatial analysis illustrates that the power
of the block prediction error is proportional to the sum of
squares of the edge gradient amplitudes. This conclusion plays
an important role in the proposed early termination threshold
definition described in Section IV.
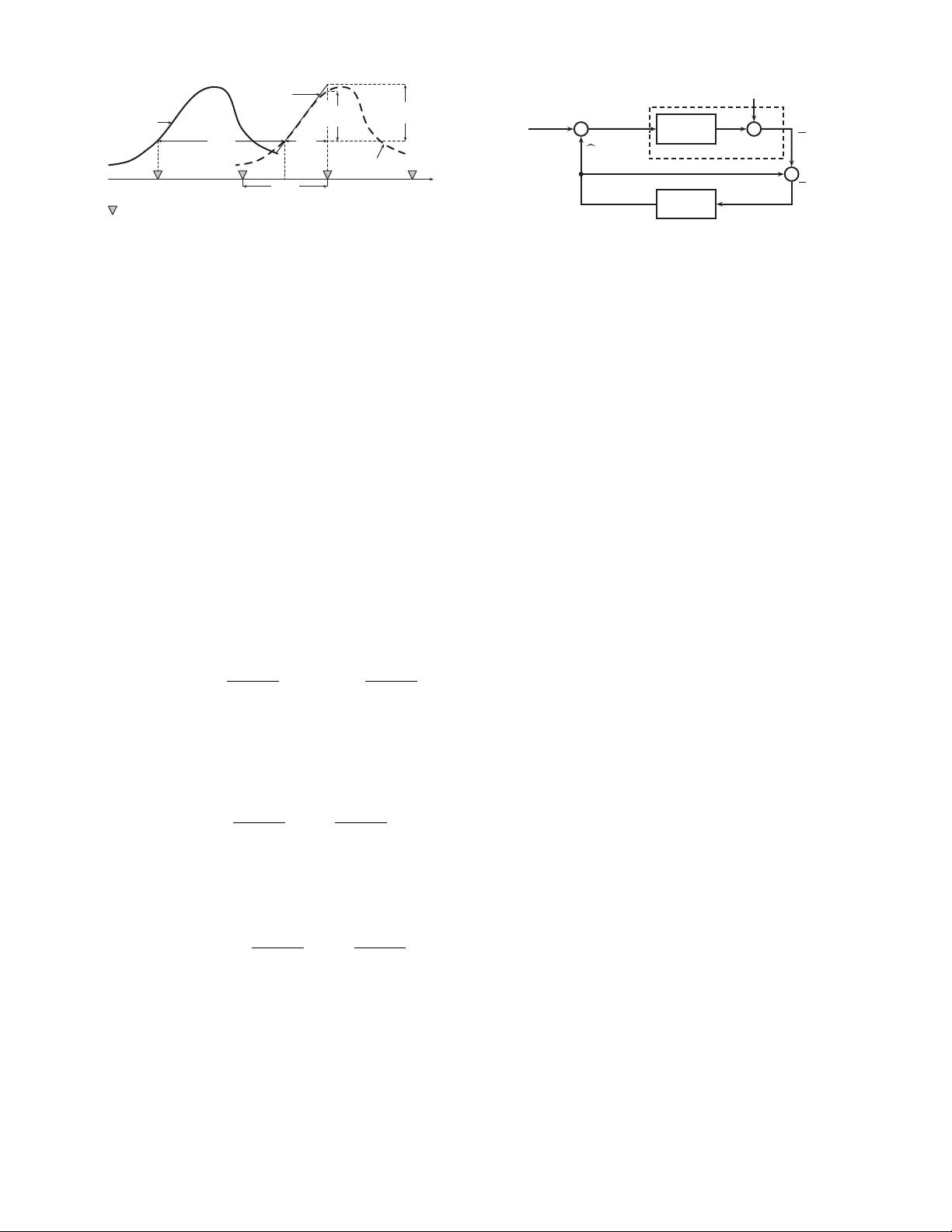
Optimum forward channel
+
+
+
+
+
S
t
(u,v) E
t
(u,v)
G(u,v)
F(u,v)
N(u,v)
E
t
(u,v)
S
t
(u,v)
S
t–1
(u,v)
Fig. 2. Model of hybrid coder with the optimum forward channel, G (u,v) =
max[0, 1 − (/(S
ee
(u,v)))] and the power spectral density of N (u,v) is
S
nn
(u,v) = max[0,(1 − (/(S
ee
(u,v)))].
Equation (3) yields two important conclusions.
1) According to the terms of displacement error |
x
|
and |
y
|, the impact of aliasing vanishes at full pixel
displacements and is at its maximum at half pixel
displacements.
2) Because of the terms of edge gradient
(
∂s
t
(i, j)/∂ x,∂s
t
(i, j)/∂y
)
, aliasing is caused by
high-frequency signals in the source image.
In practice, a picture that is rich in sharp edges must con-
tain numerous high-frequency signals. In the literature [22],
for 2-D spatial signal s(x, y),
(
∂s(x, y)/∂ x,∂s(x, y)/∂ y
)
is
defined as the local spatial frequency, which is introduced to
describe the local frequency feature in a region. The spatial
edge gradient analysis is superior to the spectral analysis
because it can efficiently reveal the local frequency nature of
the image with trivial computational overhead. Therefore, as
we shall see in Section III, when the image block contains
numerous textures, the power of its prediction errors becomes
augmented, which requires advanced coding approaches, such
as VBS and MRF techniques. Otherwise, the redundant com-
putation can be discarded with negligible coding quality
degradation. This is the essence of our homogeneity-based fast
algorithms.
III. H
OMOGENEITY-BASED REFERENCE FRAME AND
INTERMODE REDUCTION
Using rate-distortion theory, the relative homogeneity con-
cept is developed in Section III-A. Based on the relative
homogeneous block detection algorithm, the futile reference
frames and intermodes could be eliminated efficiently, which
is described in Section III-B.
A. Relative Homogeneous Block Detection Algorithm
Based on the hybrid coder model with the optimum forward
channel, as shown in Fig. 2, it is convenient to develop the
relative homogeneity concept. Capital letters, for example
S
t
(u,v), represent the discrete 2-D Fourier transforms of
the corresponding spatial signals. Let S
t
(u,v) denote the
N × N small image block to be encoded through the hybrid
coder and
S
t−1
(u,v) is the prediction signals generated from
the previously decoded image signals by the low-pass filter
F(u,v). The optimum forward channel consists of a nonideal
band-limiting filter G(u,v) and an additional noise N (u,v).
With rate-distortion theory [23], the distortion D and the
Authorized licensed use limited to: China Three Gorges University IEL Trial. Downloaded on November 3, 2009 at 22:27 from IEEE Xplore. Restrictions apply.
剩余12页未读，继续阅读
2022-08-04 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
198 浏览量
点击了解资源详情
174 浏览量
点击了解资源详情
点击了解资源详情
why19870626
- 粉丝: 1
- 资源: 8
我的内容管理
展开
