dynamic equations of the eight-rotor can be
obtained by
dH
dt
¼
H
t
þ x H ¼ M ð1Þ
where
dH
dt
represents the absolute derivative of H with
respect to the frame E, and
H
t
denotes the relative
derivative to the frame B, with the angular momen-
tum H represented as
H ¼ J x ð2Þ
and J ¼ diag I
x
, I
y
, I
z
as the moment of inertia along
x, y, and z directions. x ¼ p, q, r½
T
denotes the angu-
lar velocity with respect to the frame B. The torque
provided by the rotors thrust is expressed as
M ¼
M
x
M
y
M
z
2
6
4
3
7
5
¼
AC
T
R
2
l
2
3
þ
2
4
2
7
2
8
AC
T
R
2
l
2
1
þ
2
2
2
5
2
6
AC
D
R
3
2
1
þ
2
4
þ
2
5
þ
2
8
2
2
2
3
2
6
2
7
2
6
4
3
7
5
ð3Þ
where is air density, R denotes rotor radius,
A ¼ R
2
is rotor disk area, and C
T
, C
D
express
thrust coefficient and torque coefficient, respectively.
14
l represents the distance between the rotor and the
center of the eight-rotor.
As the eight-rotor is subjected to the external dis-
turbance that is assumed to the horizontal wind dis-
turbance, the reactive torque provided in the ith rotor
can be described as
M
i
¼ AC
D
Rð
i
R þ cosð
i
tÞÞ
2
, i ¼ 1, 2, ...,8
ð4Þ
where t is the time, denotes the inflow velocity, and
its direction is opposite to the direction of initial rotor
speed.
J
_
x ¼skðxÞJ x þ M ð5Þ
where skðxÞ called as skew-symmetric matrix is
defined by
skðxÞ¼
0 rq
r 0 p
qp 0
2
4
3
5
ð6Þ
Accordingly, substituting equation (3) into equa-
tion (5) gives
_
p
_
q
_
r
2
4
3
5
¼
½M
x
qrðI
z
I
y
Þ=I
x
½M
y
prðI
z
I
x
Þ=I
y
M
z
=I
z
2
4
3
5
ð7Þ
where I
x
¼ I
y
due to the symmetry of x and y direc-
tion in body-fixed frame B.
There is the relationship between the body angular
velocity x and the Euler rates
_
g by the fact that they
are from different coordinate systems, which can be
depicted by
_
g ¼ T x ð8Þ
where
T ¼
1 sin tan cos tan
0 cos sin
0 sin sec cos sec
2
6
4
3
7
5
ð9Þ
T is invertible when the pitch angle satisfies
6¼ð2k 1Þ=2, ðk 2 ZÞ. In the general case of
small attitude, it is reasonable to assume that T is a
unit matrix for simplicity.
The translational model calculated by the Newton-
Euler equation is derived as
m
dV
dt
¼ m
V
t
þ x V
¼ F þ DF þ W
1
ðmg E
3
Þ
ð10Þ
where V ¼½u, v, w
T
denotes the velocity with respect
to the frame B, E
3
¼½0, 0, 1
T
, m is mass of the eight-
rotor, g is acceleration due to gravity, and the thrust is
expressed by
F ¼
0
0
AC
T
R
2
ð
2
1
þ
2
2
þ
2
3
þ
2
4
þ
2
5
þ
2
6
þ
2
7
þ
2
8
Þ
2
4
3
5
ð11Þ
DF is treated as the negligible aerodynamic force.
The matrix W called the rotation matrix maps vectors
g
o
g
g
z
g
y
5
Ω
3
Ω
1
Ω
7
Ω
8
Ω
6
Ω
4
Ω
2
Ω
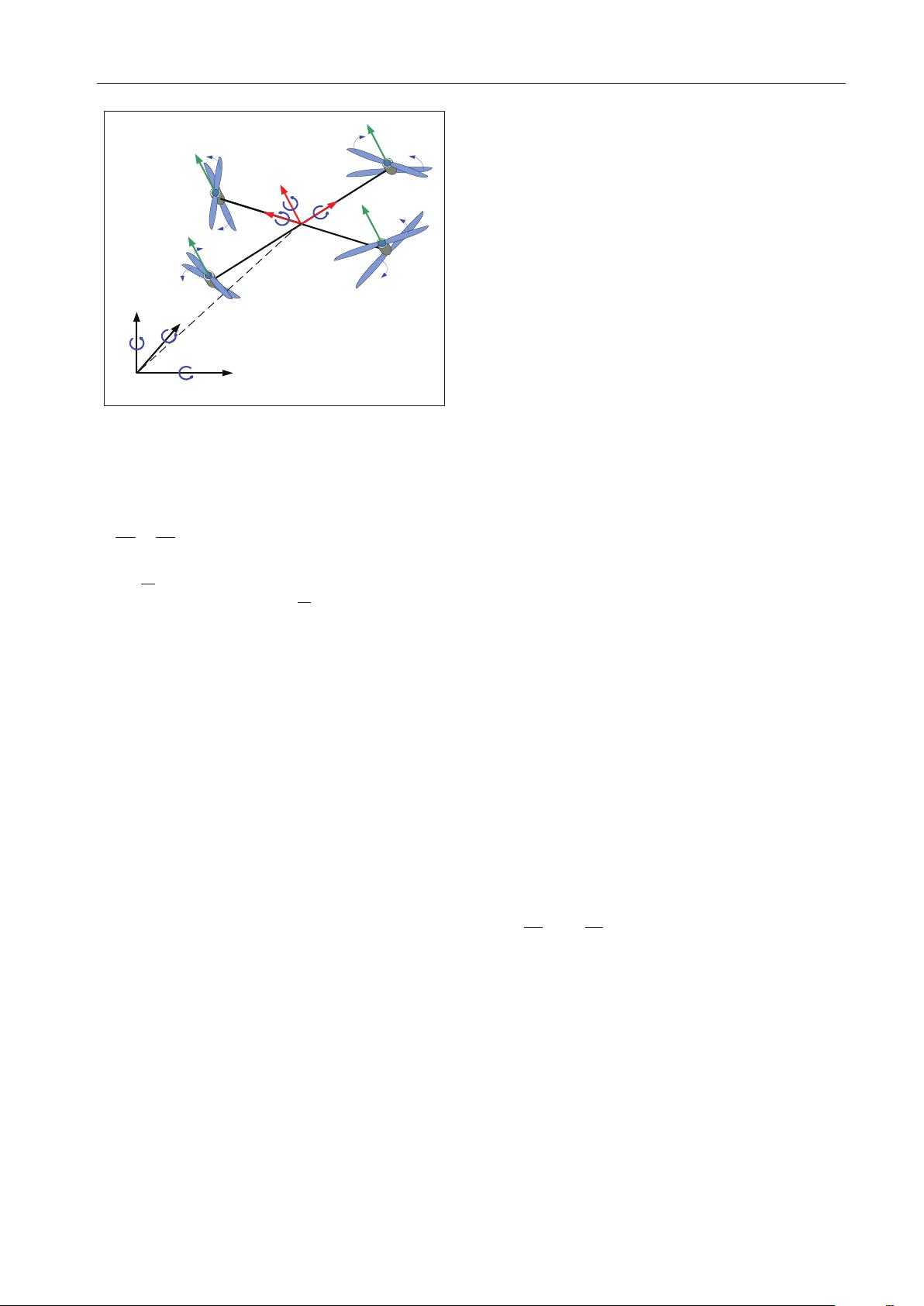
Figure 1. The scheme of the coaxial eight-rotor UAV.
Peng et al. 1663









